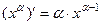|
|
Свойства линейной функции.1) Область определения — множество всех действительных чисел R. 2) Область изменения (множество значений) при k ≠ 0 — множество всех действительных чисел. При k = 0 множество значений функции состоит из одной точки b. 3) При k ≠ 0 и b ≠ 0 функция не является ни четной, ни нечетной. При k =0 (b — любое) функция четная, при b = 0 и k≠0 — нечетная. 4) Линейная функция непрерывна и дифференцируема на всей числовой оси; ее производная в каждой точке равна k. 5) Линейная функция не имеет экстремумов ни при каких значениях k и b. При k ≠ 0 критических точек нет. При k = 0 каждая точка является критической точкой функции. 6) При k > 0 линейная функция возрастает при всех 7) График линейной функции пересекает ось Оу в точке у=b. При k≠ 0 график пересекает ось Ох в точке х = —b/k, при k = 0 он параллелен оси Ох.
Обратно пропорциональная зависимость Переменную у называют обратно пропорциональной переменной х, если значения этих переменных связаны равенством у= k/x, где k — некоторое действительное число, отличное от нуля. Число k называют коэффициентом обратной пропорциональности. Если считать х независимой переменной, a y — зависимой, то уравнение у = k/x определяет у как функцию от х. График функции у = k/x называется гиперболой, Свойства функции f (х) = k/x 1) Область определения — множество всех действительных чисел, за исключением числа 0. 2) Область изменения (множество значений) — множество всех действительных чисел, за исключением числа 0. 3) Функция f (х) = k/x— нечетная, и ее график симметричен относительно начала координат. Она непрерывна и дифференцируема во всей области определения; f' (х} = — k/x2, критических точек не имеет. 4) Функция f (х) = k/x при k > 0 монотонно убывает на промежутках в (— ∞, 0) и (0, + ∞), а при k <0 монотонно возрастает на тех же промежутках.
Квадратичная функция Функция f (x) = ах2 + bх + с, где а, b, с — некоторые действительные числа (а ≠ 0), называется квадратичной функцией. График квадратичной функции называется параболой. Свойства квадратичной функции и ее график. 1) Область определения — вся числовая прямая. 2) При b ≠ 0 функция не является четной к не является нечетной. При b= 0 квадратичная функция — четная. 3) Квадратичная функция непрерывна и дифференцируема во всей области определения. 4) Функция имеет единственную критическую точку х =-b/(2а). Если а > 0, то в точке х = —b/(2а) функция имеет минимум. При х < —b/(2а) функция монотонно убывает, при х > —b/(2а) монотонно возрастает. Если а < 0, то в точке х = —b/(2а) функция имеет максимум. При х < —b/(2а) функция монотонно возрастает, при х > — b/(2а) монотонно убывает. Точка графика квадратичной функции с абсциссой хв = -b/(2а) и ординатой ув=f(xв) называется вершиной параболы. 5) Область изменения функции: при а > 0—множество значение функции—промежуток (yв;+ ∞); при а < 0 — множество значении функции — промежуток (-∞;yв) 6) График квадратичной функции пересекается с осью Оу в точке у = с. В случае, если b2— 4ас > 0, график квадратичной функции пересекает ось Ох в двух точках (различные действительные корни квадратного уравнения); если b2— 4ас = 0 (квадратное уравнение имеет один корень кратности 2), график квадратичной функции касается оси Од: в точке х = — b/(2а); если b2 — 4ас < 0, пересечения с осью Ох нет. График функции симметричен относительно прямой x = —b/(2а).
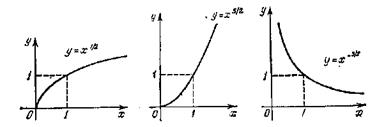
Степенной функцией называется функция вида f (х) = ха, где а — любое действительное число, называемое показателем степени. Свойства степенной функции. 1)Область определения — множество всех положительных чисел.Область изменения — множество всех положительных чисел. 2)Степенная функция непериодична, не является четной и не является нечетной. 3) Степенная функция непрерывна во всей области определения. 4) Степенная функция дифференцируема во всей области определения, и ее производная вычисляется по формуле
5) Степенная функция ха монотонно возрастает во всей области определения при а > 0 и монотонно убывает при а <0.
6) При а < 0 и а > 1 график степенной функции направлен вогнутостью вверх, а при 0 < а < 1 — вогнутостью вниз. Показательная функция Показательной функцией называется функция вида f (х) = аx, где а — некоторое положительное действительное число, называемое основанием степени. При а = 1 значение показательной функции при любом значении аргумента равно единице, и случай а = 1 далее не будет рассматриваться. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 R, при k < 0 убывает при всех х
R, при k < 0 убывает при всех х 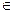 R, при k = 0 постоянна.
R, при k = 0 постоянна.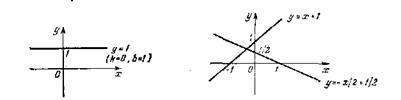
 5) График функции у = k/x при k > 0 в промежутке (0; + ∞) направлен вогнутостью вверх, а в промежутке (— ∞, 0) — вогнутостью вниз. При k < 0 промежуток вогнутости вверх — (— ∞; 0), а промежуток вогнутости вниз — (0; + ∞).
5) График функции у = k/x при k > 0 в промежутке (0; + ∞) направлен вогнутостью вверх, а в промежутке (— ∞, 0) — вогнутостью вниз. При k < 0 промежуток вогнутости вверх — (— ∞; 0), а промежуток вогнутости вниз — (0; + ∞). Степенная функция
Степенная функция