
|
|
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫМатематическим ожиданием дискретной случайной величиныназывается сумма произведений значений случайной величины на вероятности этих значений. Если случайная величина X характеризуется конечным рядом распределения:
то математическое ожидание М (X) определяется по формуле M(X)=x1p1+x2p2+x3p3+…+xnpn, или M(X)= Так как p1+p2+…+pn=1, то
M(X)= Таким образом, М (X) является взвешенной средней арифметической значений случайной величины x1, x2, ...,xn, при весах p1,p2,…,pn Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X) = M[X—M(X)]2= M(X2)- (M(X))2 Среднее квадратическое отклонение σ = Нормальный закон распределения вероятностей. Нормальный закон распределения характеризуется плотностью
Нетрудно видеть, что функция f (х) удовлетворяет, двум условиям, предъявляемым к плотности распределения: 1) f (х) > 0;
Кривая y=f(x) имеет вид, изображенный на рисунке.
Она симметрична относительно прямой х = т, максимальная ордината кривой (при х = т) равна Основные понятия теории вероятности. В теории вероятностей под испытанием (опытом)понимают комплекс определенных условий, воспроизводимый сколь угодно большое число раз, наличие которого приводит к какому-либо исходу. Исход случаен, если испытание, приводящее к какому-либо определенному исходу, имеет и другие исходы. Случайным событием(или просто событием) называется любая совокупность случайных исходов. Событие может состоять и из одного исхода, и поэтому сами исходы также можно именовать событиями. Исходы называются независимыми, если они представляют собой результаты отдельных испытаний. Случайные события обычно обозначают большими латинскими буквами А, В, С,.. Достоверным событием называют событие, которое обязательно произойдет при данном испытании. Невозможным событием называют событие, которое заведомо не произойдет при данном испытании. Так, в рассмотренном испытании с игральной костью событие, состоящее в том, что в результате испытания выпало некоторое число очков, не большее шести — достоверное, а событие, состоящее в том, что выпало семь очков,— невозможное. Два случайных события называются противоположными, если одно из них происходит в том и только том случае, когда не происходит другое. Событие, противоположное событию А, обычно обозначают Говорят, что события А1, А2,…., Ап образуют полную группу событий, если в результате данного испытания обязательно произойдет одно из них. Полная группа событий А1, А2,…., Ап называется полной группой несовместных событий, если в результате данного испытания обязательно произойдет одно и только одно событие данной группы. Среди всех возможных событий, которые в данном испытании могут произойти, можно выделить множество так называемых элементарных событий(или элементарных исходов), выделяемых из множества всех событий по следующим признакам: 1. Все они взаимно исключают друг друга, и в результате испытания обязательно происходит одно из этих событий. 2. Каково бы ни было событие А, по наступившему элементарному событию можно судить о том, наступило или не наступило событие А. Операции над событиями. Два события А и В называют равными и пишут А = В, если наступление события А влечет за собой наступление события В и, наоборот, наступление события В влечет за собой наступление события А. Объединением(или суммой) событий А и В называется событие, состоящее в наступлении события А или события В. Пересечением (или произведением) событий А и В называется событие, состоящее в одновременном наступлении как события А, так и события В. Разностью событий А и В называется событие, состоящее в том, что наступает событие А, но не наступает событие В. Разность событий А и В обозначается А \ В. Сумма, произведение и разность событий геометрически могут быть изображены так же, как сумма, произведение и разность двух произвольных множеств. Понятие вероятности. Рассмотрим опыт по бросанию монеты. Этот опыт имеет два взаимно исключающих друг друга исхода выпадение «герба» и выпадение «решетки». Обозначим эти исходы буквами «А» и «В» соответственно. Проведем серию испытаний, состоящую из п бросаний. Подсчитаем число выпадений «герба» и число выпадений «решетки». Повторим эту серию из п. испытаний несколько раз, подсчитывая каждый раз число выпадений «герба» и «решетки». Пусть число испытаний, которые привели к выпадению «герба», равно n (A). Отношение числа выпадения «герба» п (А) к числу всех испытаний п данной серии называют частотойсобытия А в данной серии опытов. Как показывает практика, при больших п частоты п (А)/п в различных сериях испытаний оказываются приблизительно одинаковыми и при достаточно больших п близкими к 1/2. Аналогичная ситуация будет и в случае бросания игральной кости: при достаточно большом числе испытаний в серии частота выпадения, скажем, шести очков в различных сериях испытаний будет примерно одинакова и близка к 1/6. Естественно, что как в примере с монетой, так и в примере с игральной костью полагалось, что монета и игральная кость геометрически правильны, сделаны из однородного материала и условия испытаний в различных сериях одинаковы. Число подобных примеров можно продолжить, но во многих случаях при многократном повторении одного и того же опыта в одних и тех же условиях частота наступления некоторого события (т. е. отношение числа опытов, в которых этот результат наблюдался, к общему числу производимых испытаний) остается примерно одинаковой и близкой к некоторому числу Р. Это число называют вероятностьюрассматриваемого события. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


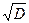
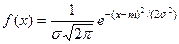
 2)
2) 
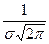 и ось абсцисс является асимптотой этой кривой. Так как
и ось абсцисс является асимптотой этой кривой. Так как  , то параметр m является математическим ожиданием случайной величины X. С другой стороны,
, то параметр m является математическим ожиданием случайной величины X. С другой стороны,  , откуда D(x)=σ2, т. е. а является средним квадратичным отклонением величины X.
, откуда D(x)=σ2, т. е. а является средним квадратичным отклонением величины X. 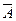 .
.