
|
|
Сочетания с повторениями.Основные понятия теории множеств и 1.3. Основные структуры. Множество– это набор, совокупность, собрание каких-либо объектов, называемых его элементами, обладающими общим для всех них характеристическим свойством. Обозначения: М – множество (принято обозначать заглавными латинскими буквами), x М = {x1, x2, x3, … , xn} – множество М состоит из элементов xi, где i =1…n, M = {Ø} – множество М – пустое, т.е. не содержит элементов, А А = В – множество А равно множеству В, т.е. множество А является подмножеством множества В, а множество В является подмножеством множества А. Способы задания множеств 1. Перечисление элементов – самый простой способ задания множества. Примером может служить список имен студентов, присутствующих на занятии. 2. Аналитический способ предполагает описание характеристического свойства множества. Пусть Р(x) – некоторое предложение, зависящее от x. Тогда запись А = {x | P(x)}, говорит о том, что множество А состоит из всех элементов x, обращающих в истинное утверждение P(x). Например, А = {x | x 3. Графический. Множество может задаваться графически. Например, А и В – множества точек круга и отрезка, соответственно:
Операции над множествами Суммой или объединением нескольких множеств называется множество всех элементов, которые являются элементами хотя бы одного из исходных множеств. Обозначается А
Пример. Если А = {1,2,4,7,8} и В = {1,3,5,6,9}, тогда А Пересечениеммножеств называется множество, состоящее из общих элементов исходных множеств. Обозначается А
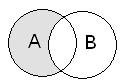
Пример. Если А = {1,2,4,7,8} и В = {1,2,5,6,9}, тогда А Разностью двух множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В. Обозначается А\В.
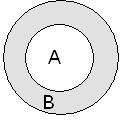
Пример. Если А = {1,2,4,7,8} и В = {1,3,5,6,9}, тогда А\В = {2,4,7,8}. Разность между множеством В и его частью - множеством А, называется дополнением множества А до множества В. Обозначается
Пример. Если А = {1,2,4} и В = {1,2,4,6,8,10}, тогда Разбиением множества А называется такая расчлененная система U непустых подмножеств множества А, что каждый элемент А является элементом некоторого (единственного) множества системы U. Пример. U = {{1},{2, 4},{7},{8}} – разбиение множества А = {1,2,4,7,8}.
Перестановки. Пусть А — некоторое конечное множество, состоящее из п различных элементов; A — {al; а2; а3;...; ап}. (I) Будем образовывать из элементов множества А упорядоченные множества. В качестве первого упорядоченного множества возьмем множество, в котором элементы расположены в порядке возрастания их номеров: {al; а2; а3;...; ап} Второе упорядоченное множество можно образовать, поменяв местами элементы а1 и а2, а все остальные элементы первого множества оставив на своих местах: { а2; al; а3;...; ап} Поменяв местами элементы а2 и а3 оставляя на своих местах все остальные элементы в первом упорядоченном множестве, получаем упорядоченное множество, отличное как от первого, так и от второго упорядоченного множества. Аналогичным способом из элементов множества А можно строить и другие упорядоченные множества. Всевозможные конечные упорядоченные множества, содержащие п различных элементов, которые можно получить из некоторого неупорядоченного множества, состоящего из п различных элементов, называются перестановками из n элементов. Таким образом, перестановка есть не что иное, как способ упорядочивания элементов некоторого конечного множества. При этом любые две различные перестановки представляют собой два различных способа образования упорядоченного множества (из данного неупорядоченного множества). Число перестановок из п элементов (которое обычно обозначается Рп) равно произведению п последовательных натуральных чисел, начиная с единицы. Это произведение имеет специальное обозначение n!(читается: n факториал): Рп= 1*2*3*...* (n— 1)*n = n! Для пустого множества принимается соглашение: пустое множество можно упорядочить только одним способом; поэтому считается, что Ø! = 1. Если в заданной перестановке поменять местами какие-либо два элемента, а все остальные элементы оставить на своих местах, то получится новая перестановка. Такое преобразование перестановки называется транспозицией. Все n!перестановок из n элементов можно расположить в таком порядке, что каждая следующая перестановка будет излучаться из предыдущей одной транспозицией, причем в качестве исходной перестановки можно выбрать любую из n! перестановок. В частности, от любой перестановки из n элементов можно перейти к любой другой перестановке из тех же элементов при помощи нескольких транспозиций. Перестановки с повторениями. Пусть А — некоторая совокупность, состоящая из п элементов: А= {al; а2; а3;...; ап} т различных типов (m Например, если A = {1, 1, 2, 3, 1, 3}, то, считая элементами первого типа единицы, элементами второго типа двойки, а элементами третьего типа тройки, имеем k1 = 3, k2 = 1, k3=2. Различные конечные совокупности, содержащие п элементов, из которых k1 принадлежат первому типу, k2— второму типу . . ., km— m-му, типу, называются перестановками с повторениями (кортежами), имеющими состав (или спецификацию) (k1,k2,k3,…,km). Число таких различных перестановок с повторениями обычно обозначается Сп (k1,k2,k3,…,km) и вычисляется по формуле Сп (k1,k2,k3,…,km)= Размещения. Пусть дано некоторое конечное множество А, состоящее из п различных элементов. Выберем некоторым образом из этих п элементов т различных элементов и будем составлять из этих m элементов различные упорядоченные множества. Конечные упорядоченные подмножества, содержащие по т элементов, выбранных из n элементов основного множества, называются размещениями из п элеметов по т элементов. Число всех возможных размещений из п элементов по т обозначается Нетрудно убедиться, что т. е. один элемент из п можно выбрать п способами, а из одного элемента можно образовать единственное упорядоченное множество. Последнее равенство можно записать с использованием символа факториала
При т = 0 получаем Сочетания. Конечные неупорядоченные множества, содержащие m различных элементов, выбранных из п элементов заданного множества, называются сочетаниями из п элементов по т. Число сочетаний из п элементов по т элементов обозначается Число сочетаний из п элементов по т равно
Сочетания с повторениями. Сочетаниями из т (различных) Элементов по п элементов с повторениями называют неупорядоченные совокупности, состоящие из п элементов, каждый из которых принадлежит к одному из т типов. Например, из трех различных элементов a1, a2, а3 можно составить следующие сочетания по два с повторениями: { a1; a1}, {a1; a2}, { a1; а3}, { a2; a2}, { a2; а3} { а3; а3}. Число различных сочетаний из m элементов по n с повторениями обозначается
Теория вероятности. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
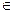 M – элемент x принадлежит множеству М,
M – элемент x принадлежит множеству М,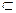 В – множество А является подмножеством множества В, т.е. все элементы множества А являются одновременно элементами множества В.
В – множество А является подмножеством множества В, т.е. все элементы множества А являются одновременно элементами множества В.

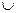 В.
В.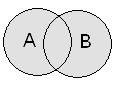
 В.
В.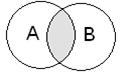
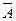 .
.
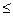 n), причем элементы одного типа, неразличимы между собой, И пусть k1 элементов принадлежат первому типу, k2 элементов принадлежат второму типу, k 3 — третьему, km— m-му типу, причем k1+k2+k3+…+km= n.
n), причем элементы одного типа, неразличимы между собой, И пусть k1 элементов принадлежат первому типу, k2 элементов принадлежат второму типу, k 3 — третьему, km— m-му типу, причем k1+k2+k3+…+km= n. 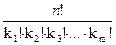
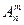
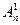 = n,
= n, ;
;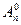 = 1, т. е. из любого множества единственным способом можно извлечь пустое множество, которое, по определению, можно упорядочить единственным способом.
= 1, т. е. из любого множества единственным способом можно извлечь пустое множество, которое, по определению, можно упорядочить единственным способом.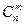 .
.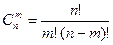
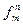 и вычисляется по формуле
и вычисляется по формуле 