|
|
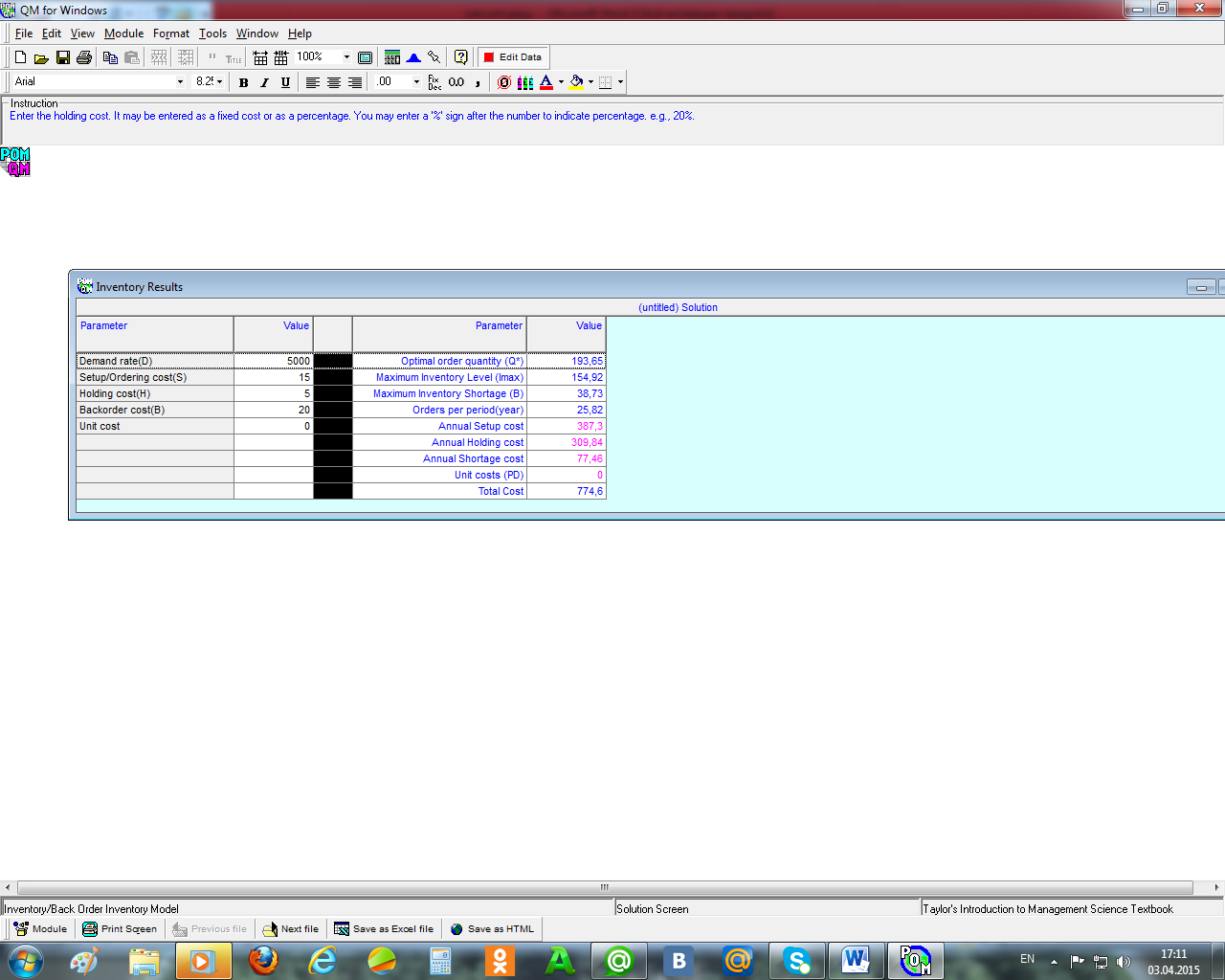
Модель запасов с дефицитомЭта модель реализует предпосылку, что иногда выгоднее иметь некоторое время неудовлетворённый спрос и за счёт этого уменьшить издержки хранения. Кроме того, в данной модели предполагается, что накопленный спрос удовлетворяется в первую очередь, и потому максимальный уровень запаса уменьшается по сравнению с оптимальным уровнем заказа на величину максимального уровня дефицита. Пусть эта модель имеет те же предпосылки, что и модель Уилсона. Обозначим через cs удельные издержки дефицита. Тогда оптимальный уровень заказа Q* и оптимальный уровень запаса I* определятся из соотношений Q* = Оптимальный уровень дефицита будет равен S* = Q*- I*. Период между поставками определится из T = Средний уровень запаса = Здесь суммарные издержки складываются из издержек заказывания, хранения и дефицита, а оптимальный уровень определяется из их минимизации. И потому издержки заказывания и хранения в оптимальной точке для этой модели не совпадают, как это было в предыдущих моделях. Продолжим решение предыдущего примера с учётом издержек дефицита. Для этого дополнительно необходимо указать издержки дефицита, которые примем равными 20. В модуле Inventory решение этой задачи показано на рисунке 7.4.
Рисунок 7.4 – Решение задачи в модуле Inventory Модель производства с дефицитом Эта модель является аналогом модели производства (оптимальной партии изделий) в предположении допущения дефицита, одно из решений задачи по этой модели приведено на рисунке 7.45.
Рисунок 7.4 – Решение задачи в модуле Inventory Это окно аналогично ранее рассмотренным. Невысокие издержки запаса здесь достигаются за счёт того, что в период пополнения запаса идёт довольно интенсивное его расходование, а потому издержки хранения малы.
Модель со скидкой за количество Эта модель предполагает, что при приобретении товара в определённых условиях цены на него снижаются. В этом случае устанавливаются границы для объёмов закупки, в пределах которых цены неизменны, а при их превышении действуют скидки.
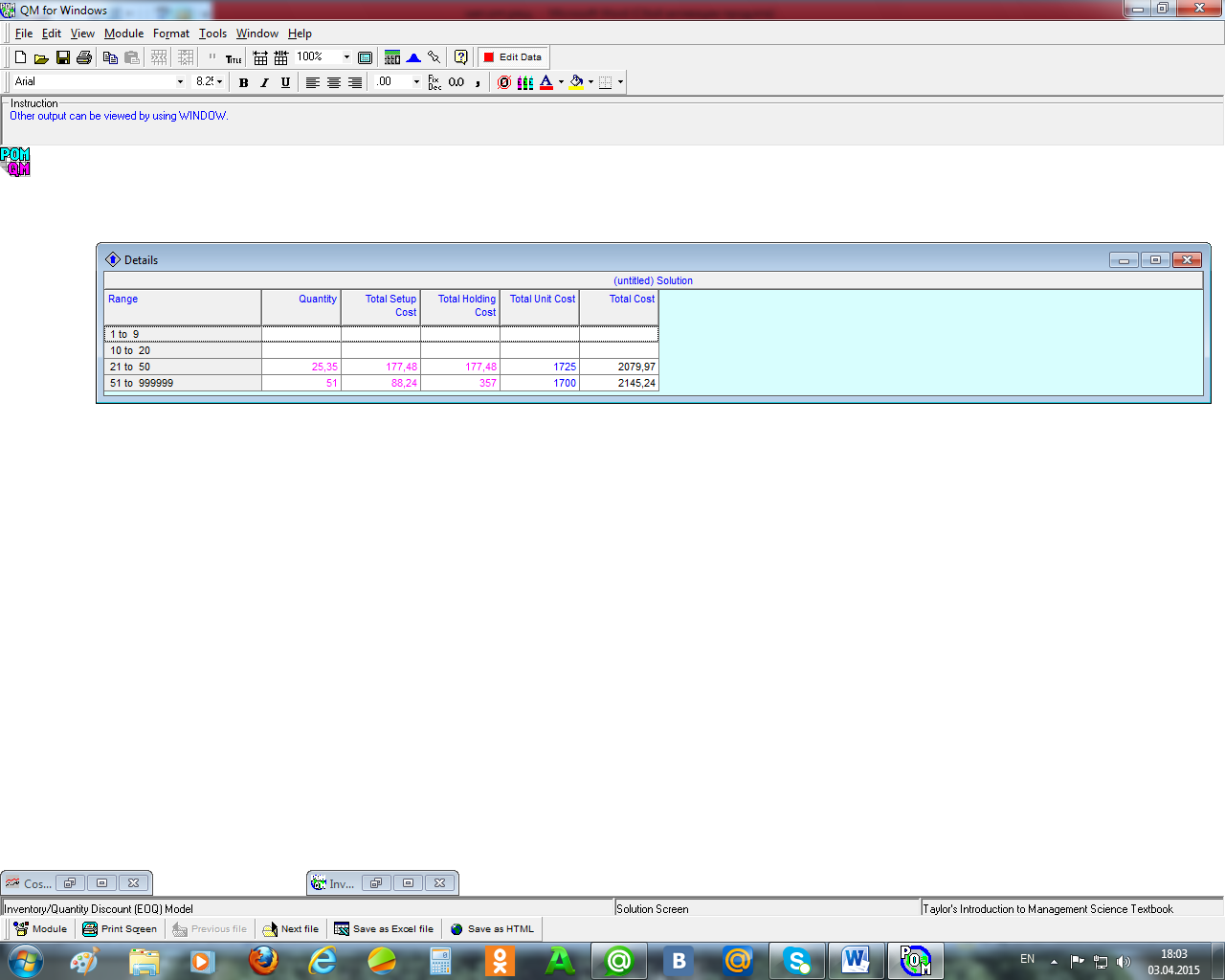
Рисунок 7.6 – Окно решения задачи управления запасами со скидкой В примере на рисунке 7.6 установлены четыре категории (интервала) для скидки с соответствующими границами и ценами. Алгоритм вычисления оптимального уровня запаса здесь усложняется. Сначала по формуле Уилсона определяется первоначальный уровень запаса Q*. Затем для каждой категории вычисляются суммарные издержки запаса, включая стоимость товара. Если Q* больше верхней границы соответствующего интервала, то за уровень запаса принимается верхняя граница соответствующего интервала, если Q* оказалось внутри соответствующего интервала, то в расчётах участвует Q*, а если Q* меньше нижней границы, то в расчётах участвует нижняя граница интервала. Оптимальным является тот уровень запаса, при котором суммарные издержки минимальны. В нашем примере оптимальное решение находится внутри интервала цен (21;50) и оптимальный уровень запаса равен 25,35, т. е. необходимо приобретать товар партиями объёмом в 25,35 по цене 17,25 денежных единиц. Остальные характеристики этой модели указаны на рисунке 8.6. На рисунке78.7 приведено исследование решения задачи в случае, когда объём заказа не менее 51 по цене в 17 у.е. При заказе в объёме, равном 51 общие издержки составят 2 145,24 у.е.
Рисунок 7.7 – Дополнительная информация о решении задачи
Задания для выполнения лабораторной работы №7 При решении задач по этой теме необходимо вычислить (с комментариями) все рассмотренные в примерах характеристики. При этом необходимо решить задачи по всем рассмотренным моделям. Исходные данные для вариантов следующие: D = 1000+10n, Co = 10+2n, Ch = 5+3n, Cs = 20+2n, где n – номер варианта. Остальную информацию (интенсивность производства, интенсивность расходования, цены, скидки и т.д.) возьмите из аналогичных решённых задач.
Библиографический список 1. Barri, Render I., Ralph V., Stair, Yr. Quantitative analysis for management. Allyn and Bacon. 4 th td. 1991. USA. 2. Бушин П. Я. Математические методы в управлении : учеб. пособие / П. Я. Бушин. – Хабаровск : РИЦ ХГАП, 1999. 3. Бушин П. Я. Математические методы и модели в экономике : учеб. пособие. – 2-е изд., перераб. и доп. / П. Я. Бушин, В. Н. Захарова. – Хабаровск : РИЦ ХГАП, 2010. 4. Вагнер Г. Основы исследования операций. Т.1 / Г. Вагнер. – М. : Мир, 1972. 5. Таха Х. Введение в исследование операций / Х. Таха. – М. : Вильямс, 2001. 6. Косоруков О. А. Исследование операций : учебник / О. А. Косоруков, А. В. Мищенко / под общ. ред. д.э.н., проф. Н. П. Тихомирова. – М. : Экзамен, 2003. 7. Эддоус М. Методы принятия решений / М. Эддоус, Р. Стенфилд. – М. : Аудит, 1997. 8. Экономико-математическое моделирование : учебник / под общ. ред. И. Н. Драгобыцкого. – М. : Экзамен, 2006. СОДЕРЖАНИЕ Введение……………………………………………………………………………3 1. Лабораторная работа № 1 (Анализмежотраслевыхсвязей) Краткие теоретические сведения……………………………..…………………..4 1.1. Схема и модель межотраслевого баланса производства и распределения продукции…………..………………………….……………………………………...4 1.2. Расчёт равновесного выпуска и равновесных цен………….…....................7 1.3. Балансы трудовых ресурсов и основных производственных фондов…….9 1.4. Постановка задачи…………………………………………….…………….10 1.5. Задания для выполнения лабораторной работы №1………….…………...11 1.6. Ход выполнения работы……………………………………….....................11 1.7. Информация для выполнения работы……………………………………...18 2. Лабораторная работа № 2 (Анализ оптимального решения задачи использования ограниченных ресурсов)………………………...............................19 2.1. Краткие сведения из линейного программирования……………………...19 2.2. Экономическая интерпретация и свойства двойственных оценок………21 2.3. Ход выполнения работы……………………………………….....................24 2.4. Задания к выполнению лабораторной работы №2………………………...33 3.Лабораторная работа №3 (Классическая транспортная задача и её модификации)……………………………………………………………..................34 3.1. Классическая транспортная задача…………………………………………37 3.2. Транспортная задача с ограничениями………………….............................39 3.3. Двухэтапная транспортная задача……………………………………….....39 3.4 Задания к выполнению лабораторной работы №3…………………………41 4. Лабораторная работа №4 (Элементы теории игр)…………………………..42 4.1. Нахождение смешанных стратегий игроков………………………………46 4.2. Сведение игры к задаче линейного программирования…………….........47 4.3. Графическое решение игры…………………………………………………48 4.4. Выбор оптимальной стратегии в условиях неопределённости (игры с природой)……………..…………………………………………………49 4.5. Задания к выполнению лабораторной работы №4………………………..51 5. Лабораторная работа №5 (Системы массового обслуживания)………......51 5.1. Общие сведения……………………………………………………………..51 5.2. Основные характеристики систем массового обслуживания……………52 5.3. Модели массового обслуживания………………………………………...54 Модель 1: (М/М/1)………………………………………………………..55 Модель 2: (М/GS/1)…………………………………….............................57 Модель 3: (М/D/1)………………………………………………………...57 Модель 4: (М/Еk/1)……………………………………………………......57 Модель 5: (М/М/S)……………………………………………………......57 Модель 6: (M/M/1) : (FCFS /m/¥)……………………………………......58 Модель 6: (M/M/1) : (FCFS /m/¥)…………………………………..........58 5.4. Пример использования этих моделей………………………………….......60 5.5. Задания для выполнения лабораторной работы №5…………..………......62 6. Лабораторная работа № 6 (Сетевое моделирование)……………………….62 6.1. Решение задач из модуля Networks………………………………………...62 6.1.1. Минимизация дерева расстояний………………............................63 6.1.2. Задача определения кратчайшего……………………....................64 6.1.3. Задача определения максимального потока в сети……................65 6.2. Управление проектами (Project Management (PERT/CPM))……………...66 6.2.1. Метод критического пути (СРМ)………………………………….69 6.2.2. PERT-сети………………………………………………………….71 6.3. СРМ с сокращением…………………………………………………………75 6.4. Составление бюджета сети………………………………………………….77 6.5. Задания для выполнения лабораторной работы № 6……………………...80 7. Лабораторная работа № 7 (Управление запасами)………………………….81 7.1. Модель определения оптимального уровня запаса……………………….82 7.2. Модель определения оптимальной партии изделий………………………84 7.3. Модель запасов с дефицитом……………………………………………….85 7.4. Модель производства с дефицитом ………………………………………..87 7.5. Модель со скидкой за количество…………………………………………87 7.6. Задания для выполнения лабораторной работы №7……………………...88 Библиографический список…………………………………………………......89 Содержание……………………………………………………………………….90
Учебное издание
Павел Яковлевич Бушин 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
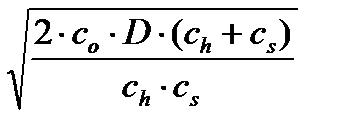 , I* =
, I* =  ,
,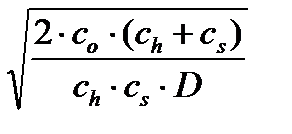 .
.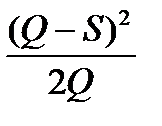 , средний уровень дефицита =
, средний уровень дефицита = 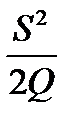 , число заказов =
, число заказов =  , тогда издержки хранения составят
, тогда издержки хранения составят