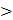|
|
Классическая транспортная задача и её модификацииТранспортная задача (ТЗ) является частным случаем задачи ЛП и может быть решена симплексным методом. Но, учитывая особенности модели ТЗ, разработаны специальные методы её решения. Один из таких методов, реализованный в рассматриваемой программе, называется методом потенциалов. Рассмотрим алгоритм решения ТЗ по этому методу. Суть ТЗ состоит в нахождении плана перевозки однородного груза от поставщиков к потребителям, минимизирующего суммарные издержки по перевозке этого груза при условии вывоза его от поставщиков и удовлетворения спроса потребителей. Математическая постановка ТЗ имеет вид: найти совокупность переменных Z = при выполнении условий:
здесь
ai – запасы i-го поставщика; bj – спрос j-го потребителя. В данной постановке ТЗ предполагается, что Решение ТЗ начинается с нахождения начального плана перевозок. Разработано несколько способов их нахождения. В программе QM реализовано три метода нахождения начального плана: метод северо-западного угла (Northwest Corner Method), метод минимальной стоимости (Minimum Cost Method), приближенный метод Вогеля (Vogel`s Approximation Method), и, если при выборе метода нахождения начального решения указать процедуру “Any Starting Method”, то программой выбирается лучший из трёх перечисленных с точки зрения значения целевой функции (обычно это – метод Вогеля). Каждый из перечисленных методов нахождения начального допустимого решения ТЗ имеет свои преимущества и недостатки, и выбор того или иного из них зависит от исходной информации. Не обсуждая подробно каждый из них, заметим, что метод северо-западного угла даёт начальное решение, расположенное в таблице транспортной задачи в направлении от левого верхнего угла к правому нижнему, и поэтому им рекомендуется пользоваться, если транспортные издержки минимальны в области этой диагонали таблицы. Метод минимальной стоимости, как правило, даёт лучшее исходное решение, если клетки таблицы ТЗ, содержащие наименьшие транспортные тарифы, расположены вне пределов такой диагонали таблицы. Приближенный метод Вогеля основан на понятии вмененных издержек, и начальное решение, полученное на его основе, как правило, даёт решение, наиболее близкое к оптимальному. Для проверки оптимальности плана в методе потенциалов используются характеристики свободных клеток таблицы ТЗ. Рассчитываются они как разность между тарифом клетки и суммой потенциалов соответствующих строк и столбцов: Eij = cij – (ui + vj), где Eij – характеристика свободной клетки (i,j); ui – потенциал i-й строки; vj – потенциал j-го столбца. Потенциалы строк и столбцов находятся из системы уравнений: cij = ui + vj , составленной по занятым клеткам таблицы. Известно, что число занятых клеток и соответственно уравнений равно m + n – 1, а число переменных ТЗ на единицу больше. Следовательно, данная система уравнений имеет одну степень свободы и для нахождения её фиксированного решения одну из переменных необходимо зафиксировать на определённом уровне. Характеристики свободных клеток не зависят от того, на каком уровне зафиксирована одна из таких переменных, поэтому в отчётах о решении задачи указываются только характеристики. Их смысл состоит в том, что они показывают, насколько изменится целевая функция, если в соответствующую свободную клетку перераспределить поставку, равную единице. Если характеристики свободных клеток неотрицательны, то соответствующий план ТЗ является оптимальным. В противном случае в клетку, имеющую наименьшую отрицательную характеристику, осуществляется перераспределение максимально возможной поставки по контуру, построенному для этой клетки. Как уже указывалось, ТЗ имеет команду Step, позволяющую поэтапно проследить решение задачи от итерации к итерации. К тому же, если ТЗ имеет неединственное оптимальное решение, то все базисные оптимальные решения можно получить, лишь используя эту команду. Если задачу решить с помощью команды Solve, то в отчёте о решении будет указано последнее оптимальное решение, предыдущие, если они существуют, не отражаются. Проиллюстрируем решение ТЗ с использованием предлагаемой программы. В диалоговом окне для создания нового файла необходимо кроме заголовка (Title) указать число источников (поставщиков) (Number of Sources) и число пунктов назначения (Number of Destinations). После ввода этой информации необходимо заполнить появившуюся таблицу исходных данных задачи. В клетки таблицы вносим тарифы, в последнюю строку (DEMAND) заносим спрос потребителей, а в последний столбец (SUPPLY) – запасы поставщиков. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (i=1,2,...,m), (j=1,2,...n), минимизирующих целевую функцию
(i=1,2,...,m), (j=1,2,...n), минимизирующих целевую функцию
 = ai, (i=1,2,...,m);
= ai, (i=1,2,...,m);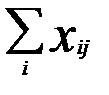 = bj, (j=1,2,...n);
= bj, (j=1,2,...n); – транспортные издержки по перевозке единицы груза;
– транспортные издержки по перевозке единицы груза;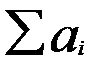 =
=  и такая модель задачи называется закрытой. Алгоритм решения ТЗ разработан для закрытых моделей, но при необходимости открытую модель легко привести к закрытой, вводя фиктивного поставщика (если
и такая модель задачи называется закрытой. Алгоритм решения ТЗ разработан для закрытых моделей, но при необходимости открытую модель легко привести к закрытой, вводя фиктивного поставщика (если