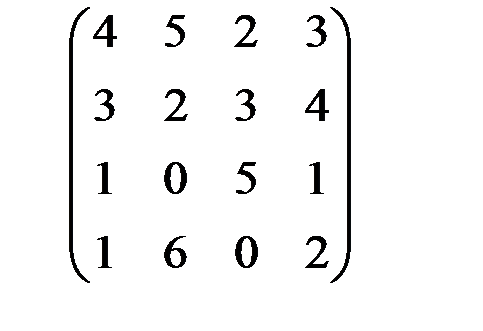|
|
Экономическая интерпретация и свойства двойственных оценокПридадим экономический смысл прямой и двойственной задачам для следующей простейшей формулировки. Будем считать, что на предприятии производится n видов продукции и при этом используются m видов ресурсов. Пусть далее
В этих обозначениях задача (2.1) – (2.3) примет вид задачи определения объёмов выпуска продукции ( Двойственная задача примет вид задачи определения оценок единицы каждого вида ресурса При такой постановке двойственные оценки приобретают определённый смысл и свойства. Сформулируем их. Свойство 1. Оценка как мера влияния ограничения на оптимальное значение целевой функции. В соответствии с этим свойством, оценка каждого вида ресурса в оптимальном плане показывает, на какую величину изменится оптимальное значение целевой функции, т.е. максимальный объём суммарного выпуска продукции, если объём соответствующего ресурса изменить на единицу. При этом надо иметь в виду, что данное свойство справедливо, если изменение ресурса не приведёт к изменению его оценки. Известно, что оценки обладают определённой устойчивостью по отношению к изменению объёма ресурса. Например, если изменить объём i-го ресурса на k единиц, то объём выпуска продукции изменится на величину Свойство 2. Оценка как мера дефицитности ресурса. Это свойство вытекает из соотношений (2.8) и (2.9). Из (2.8) следует, что если в оптимальном плане ресурс израсходован полностью (слева этого соотношения показан суммарный расход ресурса, а справа – его запас, и знак равенства указывает на то, что расход равен запасу), то оценка такого ресурса в оптимальном плане положительна. В соответствии с первым свойством, чем больше оценка ресурса, тем будет большее увеличение оптимального объёма выпуска продукции при увеличении такого ресурса на единицу. Такой ресурс будем называть дефицитным. Дефицитность здесь понимается в ином смысле, чем это обычно принято. Дефицитность здесь понимается с точки зрения вклада ресурса в увеличение выпуска продукции при его дополнительном увеличении. А из соотношений (2.9) следует, что если ресурс в оптимальном плане не израсходован (расход меньше запаса), то его оценка равна нулю. Такой ресурс будем называть недефицитным – его увеличение не приведёт к увеличению выпуска продукции в оптимальном плане. Таким образом, 2-е свойство можно сформулировать так: в оптимальном плане дефицитный ресурс имеет положительную оценку, и чем больше оценка, тем ресурс дефицитней. Недефицитный ресурс имеет нулевую оценку. Подчеркнём ещё раз, что под дефицитностью здесь понимается вклад ресурса в достижение поставленной цели. Свойство 3. Оценка как мера эффективности выпускаемой продукции. Это свойство следует из соотношений (2.10) и (2.11). В соответствии с (2.11) в оптимальном плане выпускается та продукция (выпуск больше нуля, т.е. Таким образом, это свойство можно сформулировать так: в оптимальный план включается выпуск только рентабельной продукции. Свойство 4. Оценка как средство балансировки затрат и результатов в оптимальном плане. Это свойство следует из теоремы 1. В соответствии с этой теоремой объём выпуска продукции в оптимальном плане (результат производства) равен оценке имеющихся ресурсов. Известно, что если план неоптимальный, то Z = Проиллюстрируем эти свойства на конкретном примере. При этом будем ориентироваться на решении задачи ЛП с помощью пакета прикладных задач QM for Windows. Как известно, задача ЛП решается симплексным методом, который представляет собой метод последовательного улучшения плана и реализуется в виде последовательных итераций. При необходимости эти итерации можно вывести на экран и распечатать. В этом пакете программа (ЛП) позволяет решать задачи ЛП симплексным методом без каких-либо ограничений на их вид и размерностью до 90 х 90 (по числу ограничений и переменных). Если ограничения задачи заданы в виде неравенств, то кроме основных переменных для приведения задачи к основному виду программой предусмотрено введение балансовых переменных (с положительным знаком в случае неравенства вида Необходимые сведения, нужные для анализа задачи, в дальнейшем будем приводить по мере необходимости. При вводе исходной информации в диалоговом окне необходимо предварительно указать размерность задачи: число ограничений (Number of Constraints) и число переменных (Number of variables), а также тип целевой функции (Objective) – на минимум или максимум. Задания для выполнения лабораторной работы. 1. Составить модели исходной и двойственной задач. 2. Решить задачу и вывести окна об отчёте решения. 3. Проанализировать полученное решение на основе свойств двойственных оценок. 4. Проанализировать решение задачи в условиях изменения: а) цен в границах их устойчивости; б) цен за пределами границ устойчивости; и) запасов ресурсов а в границах устойчивости; г) запасов ресурсов за пределами границ устойчивости. 5. Проанализировать решение задачи в предположении выпуска нерентабельной продукции в объёме не менее 15 единиц. 6. Проанализировать решение задачи в условиях реализации недефицитного ресурса и приобретении наиболее дефицитного ресурса для дополнительного выпуска продукции (цена ресурса соответственно равна 5, 3, 6 и 4 у.е).
Ход выполнения работы 1. Пусть в производстве 4 видов продукции участвуют 4 вида ресурсов. Известны нормы расхода каждого вида ресурса на производство единицы каждого вида продукции, цены реализации единицы каждого вида продукции и запасы каждого вида ресурса. Требуется определить план производства продукции, максимизирующий суммарную выручку от реализации произведённой продукции. Пусть А – матрица коэффициентов расхода ресурсов, В – запасы ресурсов и С – цены продукции.
Тогда модель сформулированной задачи примет вид: найти x1, x2, x3, x4, удовлетворяющие условиям:
и при которых функция Z = достигает максимума.
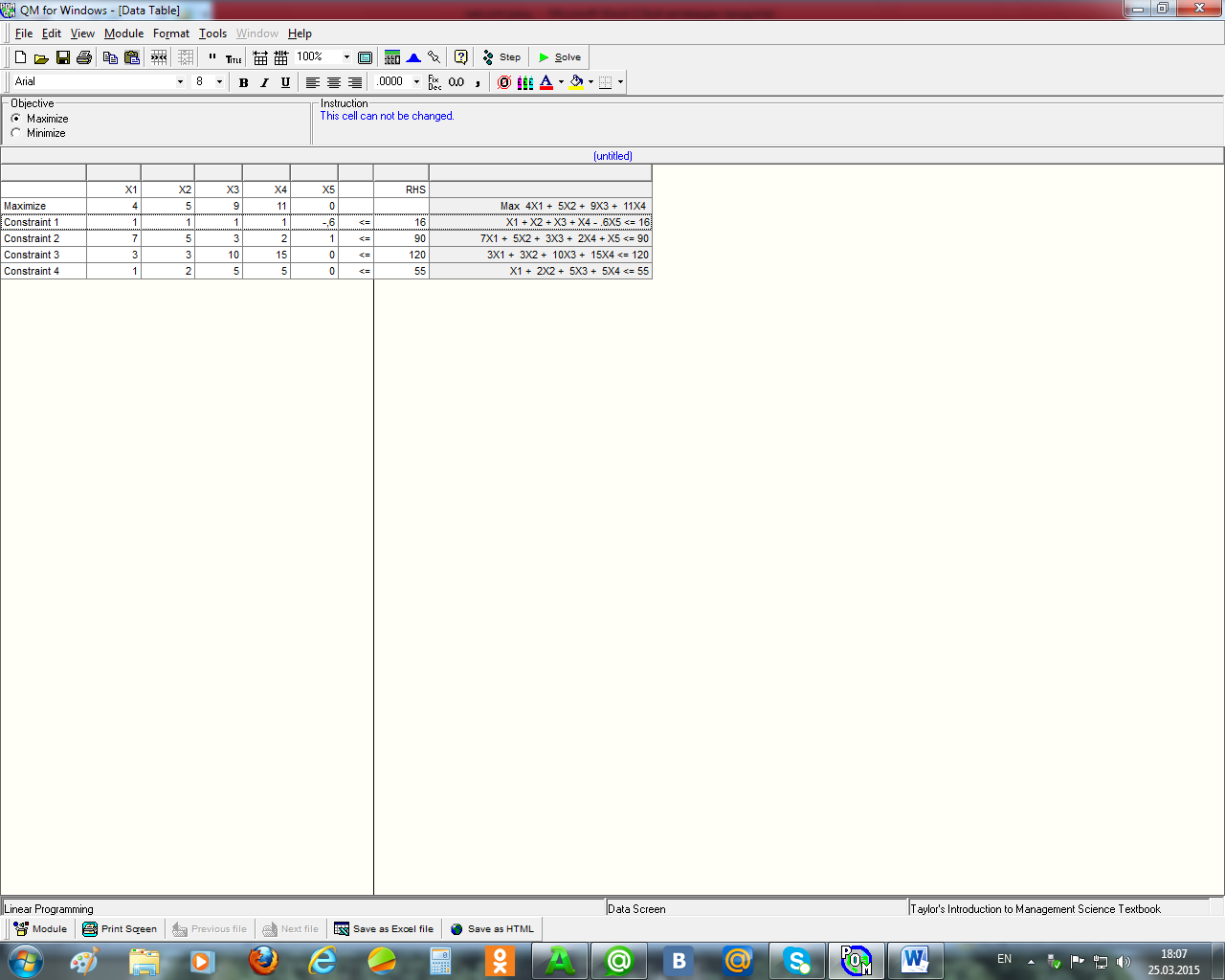
2. Введённая в модуль «линейное программирование» пакета QM for Windows эта задача примет вид, как на рисунке 2.1.
Рисунок 2.1 – Окно задачи с исходной информацией
Решение задачи с помощью пакета QM имеет нескольких окон. Приведём некоторые из них.
Рисунок 2.2 – Окно с исходной (Original Problem) и двойственной (Dual Problem) задачами
Итак, как указано в нижней части рисунка 2.2, двойственная задача заключается в нахождении двойственных оценок
при которых целевая функция W = достигает минимума. Окно с решением задачи имеет вид рисунка 2.3.
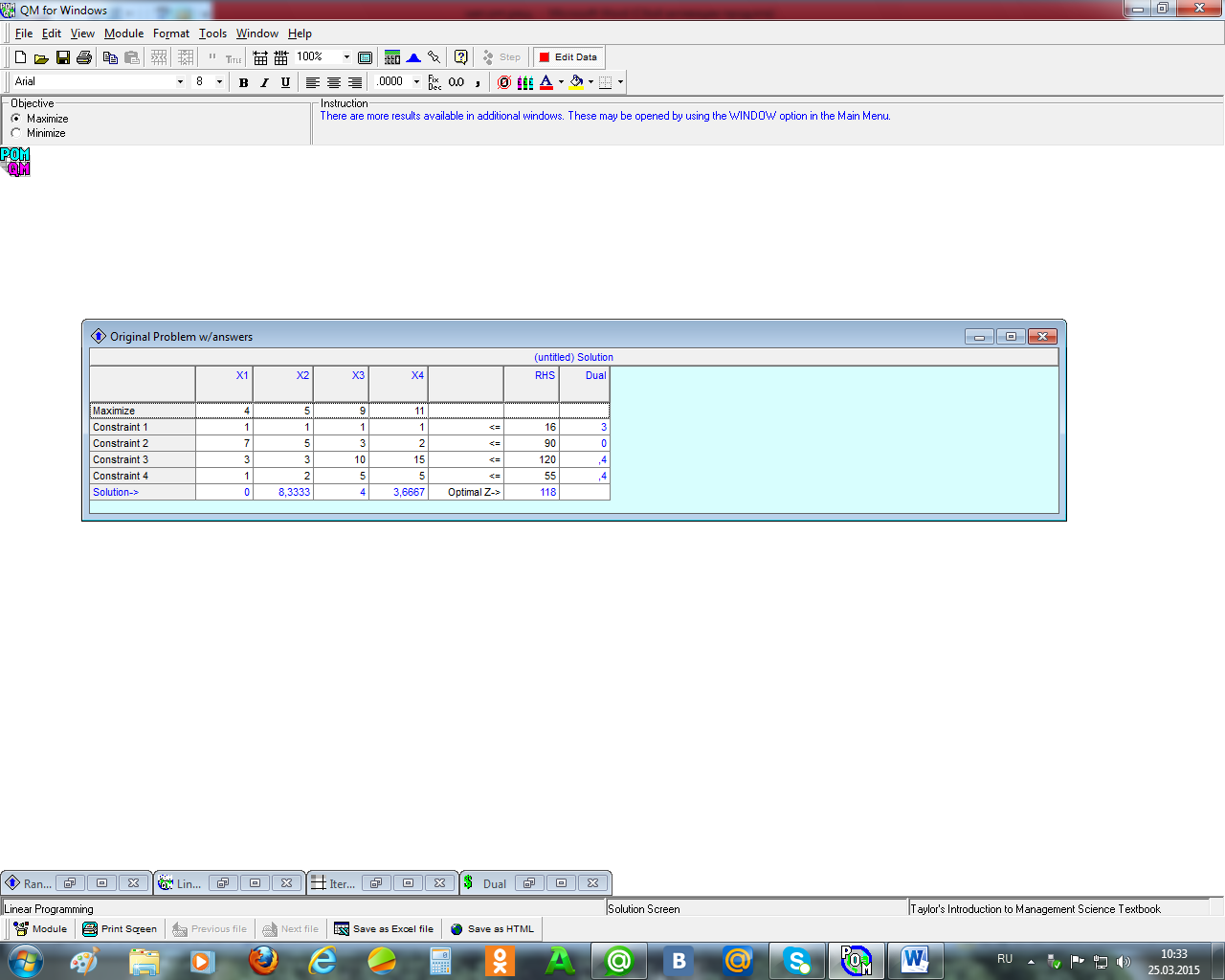
Рисунок 2.3 – Отчёт о решении прямой и двойственной задач
Это окно дублирует исходную задачу и приводит её решение (нижняя строка – Solution), а также решение двойственной задачи (крайний правый столбец – Dual). Здесь же указано оптимальное значение прямой задачи (Optimal Z = 118), а, следовательно, и оптимальное значение двойственной задачи, т.к. в соответствии с торемой1 оптимальные значения прямой и двойственной задач совпадают.
Рисунок 2.4 – Подробный отчёт о решении прямой задачи На рисунке 2.4 приведён подробный отчёт о решении прямой задачи. Как известно, симплексным методом можно решать канонические задачи ЛП, т.е. когда система ограничений приведена к базису, а правые части ограничений неотрицательны. Чтобы привести нашу систему ограничений к такому виду, потребовалось в каждое неравенство ввести балансовую переменную. Обозначаются они через slack. Таким образом, определяем, что оптимальное решение исходной (прямой) задачи равно На рисунке 2.5 приведены границы устойчивости двойственных оценок прямой и двойственной задач. Известно, что двойственные оценки довольно устойчивы по отношению к небольшим изменениям правых частей задачи. В нашем случае для прямой задачи правые части ограничений – это запасы ресурсов, а для двойственной – цены продукции. В силу симметричности прямой и двойственной задач переменные исходной задачи – это двойственные оценки двойственной задачи. Итак, в верхней части таблицы 2.5 указаны границы устойчивости цен, а в нижней – запасов ресурсов.
Рисунок 2.5 – Границы устойчивости двойственных оценок Структура таблицы на рисунке 2.5 следующая. Во втором столбце таблицы указаны значения переменных в оптимальном решении прямой и двойственной задач (Value/Dual Value), затем столбец значений балансовых переменных этих задач (Reduced Cost/Slack), затем столбец значений правых частей ограничений этих задач (соответственно – цены продукции и запасы ресурсов) и, наконец, нижняя и верхняя границы устойчивости этих величин. Пока цены продукции и запасы ресурсов, изменяясь, не выйдут за пределы этих границ, двойственные оценки прямой и двойственных задач меняться не будут.
3. Проанализируем решение нашей задачи, используя свойства двойственных оценок. В соответствии с первым свойством, если изменить объём первого ресурса на единицу, то оптимальное значение целевой функции (суммарный объём выпуска продукции) изменится на 3 единицы (на оценку единицы этого ресурса). Изменение 2-го ресурса на единицу не приведёт к изменению выпуска продукции (его оценка равна нулю). Соответственно, изменение 3-го и 4-го ресурсов на единицу приведёт к изменению объёма выпуска продукции на 0,4 единицы. В соответствии со вторым свойством дефицитными у нас являются 1-й, 3-й и 4-й ресурсы, т.к. их оценки в оптимальном плане положительны. Недефицитным является 2-й ресурс – его оценка равна нулю. Наиболее дефицитным является 1-й ресурс, т.к. его оценка наибольшая. Проверим 2-е ограничение по недефицитному ресурсу, подставив в него значения переменных из оптимального плана:
Получим 7*0+5*8,333+3*4+2*3,667 = 61, что меньше 90 на 29 единиц, а это и есть значение балансовой переменной во втором ограничении в оптимальном решении (см. рисунок 2.5, 3-ю снизу строку в столбце slack). Если провести проверку других ограничений, то они выполнятся как строгие равенства. В соответствии с 3-м свойством рентабельной является продукция 2-го, 3-го и 4-го видов (выпускается соответственно в объёмах 8,3 4 и 3,7 единиц), а продукция 1-го вида не выпускается, т.е. является нерентабельной. Проверим это, подсчитав оценку ресурсов на выпуск единицы этой продукции. Для этого подставим в первое ограничение двойственной задачи значения оценок из оптимального плана:
Получим 1*3+7*0+3*0,4+1*0,4 = 4,6, что больше 4 на величину 0,6, а это и есть значение балансовой переменной в первом ограничении в оптимальном плане (см. рисунок 2.5 первая строка сверху). Если провести проверку других ограничений, то они выполнятся как строгие равенства. В соответствии с 4-м свойством и теоремой 1. Zmax = Wmin. Проверим это, подставив оптимальные значения переменных прямой и двойственной задач в их целевые функции. Z = Zmax = 4*0+5*8,333+9*4+11*3,666 = 118. W = Wmin = 16*3+90*0+120*0,4+55*0.4 = 118. Что и требовалось показать.
4. Проверим устойчивость двойственной оценки на примере первого ресурса. Его объём может меняться в пределах 11 Решение задачи примет вид (рисунок 2.6). Как видим, оценки ресурсов остались прежними, хотя объёмы выпуска продукции изменились. Кроме того, значение целевой функции стало равно 127, что можно было получить и не решая задачу. Изменение на единицу этого ресурса вызывает изменение Zmin на 3ед., а изменив объём ресурса на три единицы (в пределах границ устойчивости) Zmin изменится на 3*3=9 единиц, т.е. к 118 добавляется 9, чему и равна целевая функция в изменённой задаче (127).
Рисунок 2.6 – Решение задачи при изменении ресурса в границах устойчивости Увеличим объём этого ресурса на 5 единиц, тем самым выйдем за пределы границ устойчивости. Получим (рисунок 2.7)
Рисунок 2.7 – Решение задачи при изменении ресурса за пределами границ устойчивости
Как и ожидалось, изменились оценки ресурсов и структура выпуска продукции (вместо первого продукта нерентабельным стал третий, а недефицитным стал первый ресурс). Будем теперь менять цену продукции. В оптимальном плане исходной задачи нерентабельной была первая продукция. Увеличим её цену в пределах границы устойчивости, установив равной 4,5, решив задачу, получим (рисунок 2.8).
Рисунок 2.8 – Решение задачи при изменении цены в границах устойчивости
Как и ожидалось, ничего не изменилось. Первый продукт по-прежнему нерентабельный. Изменим его цену за пределами границ устойчивости. Получим (рисунок 2.9).
Рисунок 2.9 – Решение задачи при изменении цены за пределами границ устойчивости
Теперь первый продукт стал рентабельным, нерентабельным – второй.
5. Предположим далее, что в условиях исходной задачи требуется выпустить нерентабельной продукции в объёме 3 единиц, не меняя её цену. Проверим, как это отразится на оптимальном плане. У нас нерентабельная 1-я продукция, поэтому дополнительное ограничение будет иметь вид
Рисунок 2.10 – Условие задачи с дополнительным ограничением
Решим эту задачу (рисунок 2.11). Как видим, первый вид продукции выпускается в объёме 3 единиц, как и было задано. Объёмы выпуска других видов продукции изменились: 2-го и 4-го видов уменьшились, а 3-го вида увеличился.
Рисунок 2.11 – Решение задачи с дополнительным ограничением
Оценка нового ограничения (-0,6) показывает, что выпуск единицы 1-й продукции уменьшает целевую функцию (объём выпуска продукции) на 0,6 единиц. И соответственно целевая функция уменьшилась на 3*0,6=1,8 единиц и стала равна 116,2.
6. Вернёмся к исходной задаче и зададимся целью увеличить выпуск продукции, реализовав остаток недефицитного ресурса и приобретя на полученную выручку наиболее дефицитный первый ресурс. Пусть, например, цена первого ресурса равна 5, а второго – 3. Через x5 обозначим объём реализованного 2-го ресурса. Тогда второе ограничение примет вид
Т.е. этот ресурс расходуется на выпуск продукции плюс на продажу в объёме х5. Изменится и первое ограничение: продав второй ресурс по цене 3, выручим 3*х5. На эту сумму приобретём первый ресурс по цене 5. Объём приобретённого ресурса будет равен (3*х5)/5, т.е. 0,6х5. Таким образом, объём первого ресурса станет равным 16+0,6х5, и первое ограничение примет вид.
Перепишем его в виде
Добавим столбец для переменной х5, и задача примет вид (рисунок 2.12).
Рисунок 2.12 – Модель задачи с изменёнными условиями Решим её (рисунок 2.13).
Рисунок 2.13 – Решение задачи с изменёнными условиями
Как видим, продали второй ресурс в объёме 6,3 единиц (
Задания к выполнению лабораторной работы №2
Варианты заданий возьмите из этой таблицы
Таблицы норм затрат ресурсов таблица 1 таблица 2 таблица 3 таблица 4
Запасы ресурсов
Варианты цен реализации продукции
Лабораторная работа №3 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – нормы расхода i-го вида ресурса на производство единицы j-го вида продукции;
– нормы расхода i-го вида ресурса на производство единицы j-го вида продукции; – объём i-го вида ресурса;
– объём i-го вида ресурса; – цена единицы j-го вида продукции;
– цена единицы j-го вида продукции;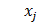 – искомые объёмы выпуска продукции j-го вида.
– искомые объёмы выпуска продукции j-го вида.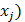 при известных нормах затрат ресурсов (
при известных нормах затрат ресурсов ( 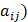 так, что расход каждого вида ресурса не превышал бы имеющегося запаса ресурса (
так, что расход каждого вида ресурса не превышал бы имеющегося запаса ресурса (  , и при этом суммарный объём выпуска продукции (Z) должен быть максимальным.
, и при этом суммарный объём выпуска продукции (Z) должен быть максимальным. , таких, что оценка ресурса на выпуск единицы каждого вида продукции должна быть не меньше цены единицы этого продукта (
, таких, что оценка ресурса на выпуск единицы каждого вида продукции должна быть не меньше цены единицы этого продукта (  , а суммарная оценка всех ресурсов (W) была бы минимальной.
, а суммарная оценка всех ресурсов (W) была бы минимальной. , если это изменение ресурса не вышло за границу устойчивости двойственной оценки. В противном случае придётся последствия такого изменения определять, пересчитывая задачу заново. Границы устойчивости двойственных оценок определяются по определённому алгоритму и выдаются при решении задачи ЛП любым пакетом программ.
, если это изменение ресурса не вышло за границу устойчивости двойственной оценки. В противном случае придётся последствия такого изменения определять, пересчитывая задачу заново. Границы устойчивости двойственных оценок определяются по определённому алгоритму и выдаются при решении задачи ЛП любым пакетом программ. ), оценка суммарных затрат ресурсов на выпуск единицы которой равна цене единицы этого продукта. Такую продукцию будем называть рентабельной. А в соответствии с (2.10) продукция в оптимальном плане не выпускается (
), оценка суммарных затрат ресурсов на выпуск единицы которой равна цене единицы этого продукта. Такую продукцию будем называть рентабельной. А в соответствии с (2.10) продукция в оптимальном плане не выпускается (  ), если оценка ресурсов на выпуск единицы такой продукции больше цены. Под рентабельностью здесь понимается равенство оценки ресурсов на выпуск единицы продукции цене единицы этой продукции.
), если оценка ресурсов на выпуск единицы такой продукции больше цены. Под рентабельностью здесь понимается равенство оценки ресурсов на выпуск единицы продукции цене единицы этой продукции.
 W =
W = 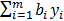 , т.е. «затраты» превышают результат.
, т.е. «затраты» превышают результат.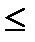 и отрицательным – при знаке
и отрицательным – при знаке  ). Обозначаются они в отчётах о решении задачи по-разному, в зависимости от того, с каким знаком вошли в ограничения. Если со знаком минус, то через “surplus” (излишек), а если со знаком плюс, то через “slack” (избыток), с соответствующими индексами. Если после введения балансовых переменных исходный базис неочевиден, то предусмотрено введение искусственных балансовых переменных. Искусственные переменные обозначаются через “artfcl”, с соответствующими индексами.
). Обозначаются они в отчётах о решении задачи по-разному, в зависимости от того, с каким знаком вошли в ограничения. Если со знаком минус, то через “surplus” (излишек), а если со знаком плюс, то через “slack” (избыток), с соответствующими индексами. Если после введения балансовых переменных исходный базис неочевиден, то предусмотрено введение искусственных балансовых переменных. Искусственные переменные обозначаются через “artfcl”, с соответствующими индексами.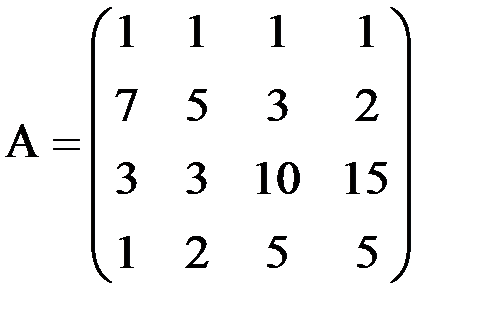 ;В=
;В=  С=
С=  .
.

 0, (j=1,2,3,4),
0, (j=1,2,3,4),


 , (i = 1,2,3,4), удовлетворяющих условиям:
, (i = 1,2,3,4), удовлетворяющих условиям: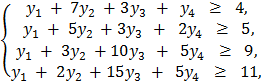


 = (0;8,3; 4; 3,7). Первая переменная в оптимальном плане равна нулю (
= (0;8,3; 4; 3,7). Первая переменная в оптимальном плане равна нулю (  = 0), следовательно, не входит в базис в оптимальном решении, а остальные переменные не равны нулю, следовательно, являются базисными, что и указано в верхней части рисунка 2.4. В нижней части рисунка 2.4 указан статус балансовых переменных. Тот факт, что slack 2 = 29, означает, что в оптимальном решении левая часть второго ограничения меньше правой части на эту величину. А остальные ограничения выполняются как строгие равенства.
= 0), следовательно, не входит в базис в оптимальном решении, а остальные переменные не равны нулю, следовательно, являются базисными, что и указано в верхней части рисунка 2.4. В нижней части рисунка 2.4 указан статус балансовых переменных. Тот факт, что slack 2 = 29, означает, что в оптимальном решении левая часть второго ограничения меньше правой части на эту величину. А остальные ограничения выполняются как строгие равенства.
 .
. .
.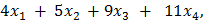
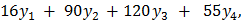
 (см. рисунок 2.5), и в этом случае оценка ресурса не изменится и в соответствии с 1-м свойством будет показывать, насколько изменится целевая функция, если объём ресурса изменить в пределах границ устойчивости. Увеличим его запас на 3 ед., т.е. сделаем равным 16+3=19.
(см. рисунок 2.5), и в этом случае оценка ресурса не изменится и в соответствии с 1-м свойством будет показывать, насколько изменится целевая функция, если объём ресурса изменить в пределах границ устойчивости. Увеличим его запас на 3 ед., т.е. сделаем равным 16+3=19.



 Введём дополнительную строку, в которой запишем, что х1 должен быть не менее трёх. Задача примет вид (рисунок 2.10).
Введём дополнительную строку, в которой запишем, что х1 должен быть не менее трёх. Задача примет вид (рисунок 2.10).

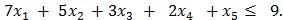
 .
. .
.

 и за счёт этого увеличили выпуск 2-й и 4-й продукции, а выпуск 3-й продукции уменьшился, но общий объём выпуска увеличился и стал равным 1293478. Поскольку все двойственные оценки в новом плане положительны, то все ресурсы в нём израсходованы полностью (стали дефицитными).
и за счёт этого увеличили выпуск 2-й и 4-й продукции, а выпуск 3-й продукции уменьшился, но общий объём выпуска увеличился и стал равным 1293478. Поскольку все двойственные оценки в новом плане положительны, то все ресурсы в нём израсходованы полностью (стали дефицитными).