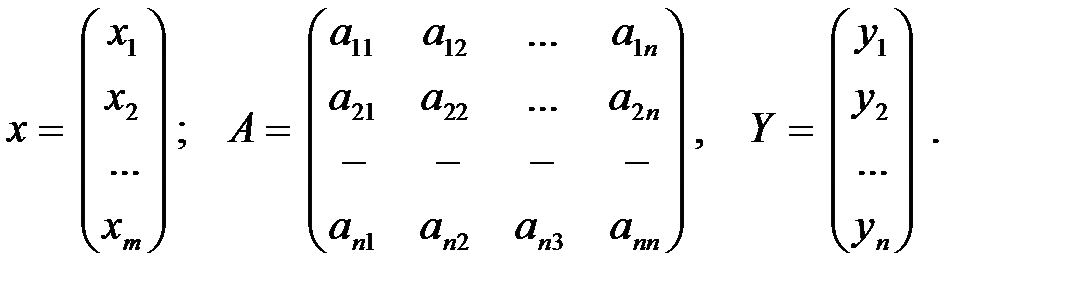|
|
Схема и модель межотраслевого баланса производства и распределения продукцииМетоды оптимальных решений Практикум по выполнению лабораторных работ
Хабаровск 2015 УДК 519.95 ББК В 1 Б 94 Бушин П. Я. Методы оптимальных решений : практикум по выполнению лабораторных работ / П. Я. Бушин. – Хабаровск : РИЦ ХГАЭП, 2015. – 92 с.
Содержание практикума в основном соответствует требованиям государственных образовательных стандартов высшего профессионального образования по направлению подготовки «Менеджмент» и «Экономика» квалификации (степень) «бакалавр» очной и заочной форм обучения и программе дисциплин «Методы оптимальных решений» и «Математические методы в управлении». В практикуме приводятся краткие теоретические сведения по рассматриваемым темам, решаются задачи с конкретной информацией, анализируются результаты решения с рекомендациями по принятию решений на основе этого анализа. Все расчёты проводятся с использованием компьютерных программ. Приводятся рекомендации по их применению и вводу исходной информации, а также указываются возможные окна отчётов, необходимые для выполнения лабораторных работ. Практикум предназначено для обучающихся по направлению «Менеджмент и Экономика» по очной и заочной форм обучения, кроме того, он может быть использован и магистрантами разных направлений обучения и специалистами, принимающими участие в выработке управленческих решений на основе методов оптимальных решений. Рецензенты: Р. В. Намм, доктор физ.-мат. наук, профессор, гл. научный сотрудник ВЦ ДВО РАН В. А. Кузнецов, канд. физ.-мат. наук, доцент кафедры ММиИТ ДВИ-филиал РАНХиГС
Утверждено издательско-библиотечным советом академии в качестве учебного пособия
ВВЕДЕНИЕ Современному экономисту и менеджеру для принятия решений в своей профессиональной деятельности необходимо владеть методами количественного моделирования анализируемых процессов для разработки альтернатив эффективного развития и управления этими процессами. В предлагаемом практикуме основное внимание уделено вопросам математического моделирования на основе балансовых и оптимизационных моделях. К ним относятся модели межотраслевых связей, модели на основе линейного программирования, сетевое моделирование, теория игр, теория массового обслуживания, оптимальное управление запасами и др. Для построения математической модели необходимо иметь чёткое представление о цели функционирования исследуемой системы и располагать информацией об ограничениях, которые определяют область допустимых значений управляемых переменных. Анализ модели должен привести к определению наилучшего управляющего воздействия на объект управления при выполнении всех установленных ограничений. Выполнение лабораторных работ, предлагаемых в практикуме, должно дать студентам достаточное первоначальное представление о математическом аппарате разработки методов принятия решений, а также показать сферы приложений этих методов на наглядных примерах.
Лабораторная работа № 1 Анализмежотраслевыхсвязей Краткие теоретические сведения Система балансов как экономико-математическая модель является незаменимым рабочим инструментом государственного регулирования экономики. Обычно составляются отчётные и плановые балансы. Отчётные балансы строятся на основе отчётных статистических данных, и их анализ помогает правильно оценить сложившиеся пропорции в экономике страны и сформулировать основные задачи на следующий период. Плановые балансы позволяют выработать рекомендации по сбалансированности всех элементов общественного производства в будущем периоде и установить соответствие потребностей и ресурсов хозяйственной системы, которые сложатся в экономике в случае выполнения рекомендаций. Анализ плановых балансов позволяет определить возможные темпы и пропорции развития экономики и установить, в какой степени тот или иной вариант расчётов соответствует социально-экономическим задачам планового периода, в какой мере в нём учтены требования объективных экономических законов. Схема и модель межотраслевого баланса производства и распределения продукции Введём необходимые для дальнейшего понятия. Промежуточный продукт (промежуточный спрос) – эточасть валового продукта (спроса), представляющего собой закупки i-го вида продукции j-ми отраслями в качестве исходных материалов, т.е. это продукт, который поступает из i-й отрасли в j-ю для дальнейшей переработки в текущем периоде. Будем обозначать его через xij. Конечный продукт (конечный спрос) – это часть общего спроса, представляющая закупки продуктов, выходящих из сферы производства в область конечного использования на потребление и инвестиции. Будем обозначать его через yi. Условно-чистая продукция или добавленная стоимость – это созданная стоимость, состоящая из заработной платы, предпринимательского дохода, различного вида налогов и амортизации. Условно-чистая продукция – это стоимостный эквивалент конечной продукции. Будем обозначать его через zj. МОБ представляет собой экономико-математическую модель процесса воспроизводства, которая в развёрнутом виде отражает взаимосвязи по производству, распределению, потреблению и накоплению каждого вида продукции в единстве материально-вещественного и стоимостного аспектов воспроизводства. Он состоит из двух таблиц, наложенных одна на другую. В первой из них в отраслевом разрезе представлена структура затрат, или структура используемых ресурсов, необходимых для каждой отрасли. В том числе и элементы условно-чистой продукции (добавленной стоимости). Во второй – распределение выпуска каждого вида продукции на нужды промежуточного (текущего производственного) и конечного использования. Затраты отражены по столбцам общей таблицы, а распределение – по строкам. Пересекающаяся часть этих двух таблиц образует так называемую “шахматку”, или первый квадрант общей схемы МОБ. Строки и столбцы “шахматки”, имеющие одинаковые номера, характеризуют процесс производства (по столбцам) и распределения (по строкам) продукции одной и той же отрасли на нужды текущего производственного потребления. В пределах “шахматки” (I квадранта МОБ) отражается внутрипроизводственный оборот (промежуточные затраты – промежуточный выпуск) предметов труда и услуг. Рассмотрим общую схему МОБ, которая в стоимостном исчислении состоит из четырёх разделов (квадрантов) (таблица 1.1).
Таблица 1.1 – Таблица межотраслевого баланса
В I и II квадрантах отражаются важнейшие материально-вещественные взаимосвязи и пропорции национальной экономики, выраженные в стоимостных измерителях – отраслевая и материально-вещественная структура фондов текущего производственного потребления и конечной продукции. Каждая строка здесь характеризуется следующим балансом: Выпуск продукции = Промежуточный спрос + Конечный спрос, или где xi – валовой продукт i-й отрасли; n – число отраслей. В I и III квадрантах находят отражение важнейшие стоимостные пропорции по производству национального продукта. Здесь отражена стоимостная отраслевая структура затрат или структура используемых ресурсов, необходимых для каждой отрасли. Каждый столбец здесь характеризуется следующим балансом: Расходы отрасли = Промежуточные затраты + добавленная стоимость, что в математической записи выглядит так:
Итоги одноимённых строк и столбцов таблицы МОБ равны, т.е. равны выпуск и расходы отрасли:
а, следовательно, общая сумма конечного спроса равна общей сумме добавленной стоимости:
Равенство (1.1) называется системой уравнений распределения продукции, равенство (1.2) – системой уравнений производства продукции, а (1.3) – основное балансовое соотношение. Будем считать, что объёмы промежуточного производственного потребления прямо пропорциональны объёмам производства продукции потребляющих отраслей: xij = aij xj (i,j = где коэффициентами пропорциональности aij являются коэффициенты прямых материальных затрат, определяемые из соотношений: aij = xij / xj (i,j = Из (1.4) следует и смысл этих коэффициентов; они показывают объём материальных ресурсов i-го вида, необходимый для производства единицы валового продукта j-го вида. После подстановки (1.4) в (1.1) получаем
Это и есть система уравнений модели В. Леонтьева “затраты-выпуск”, называемая статической моделью МОБ. Рассчитаем равновесный выпуск, найдя решение xi (i = Запишем систему уравнений (2.6) в матричной форме: X = AX + Y , (1.6а)
(1.6а) называется моделью затраты-выпуск В Леонтьева.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Бушин П. Я., 2015
Бушин П. Я., 2015




 .
. 






 , (1.1)
, (1.1) (1.2)
(1.2)
 ( при i = j ),
( при i = j ),
 . (1.3)
. (1.3)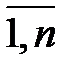 ), (1.4)
), (1.4) . (1.6)
. (1.6)