
|
|
Модели массового обслуживанияДля классификации моделей массового обслуживания будем пользоваться обозначениями, введёнными Кендаллом. В соответствии с этими обозначениями для характеристики модели массового обслуживания достаточно указать значения шести параметров в следующем формате: (закон распределения для входящего потока / закон распределения длительности обслуживания / число каналов обслуживания): (дисциплина очереди / максимальная длина очереди / ёмкость источника, генерирующего заявки на обслуживание). Обычно принимаются следующие обозначения для закона распределения входящего потока: М – пуассоновское (марковский случайный процесс); Д – детерминированный (с фиксированным интервалом времени между моментами последовательных поступлений заявок в систему); Еk – Эрланга с параметром k; G – произвольное. Для обозначения закона распределения времени обслуживания обозначения следующие: М – отрицательный экспоненциальный; Д – детерминированный (с фиксированной продолжительностью обслуживания); Еk – Эрланга с параметром k; GS – общее распределение произвольного вида. Для рассматриваемых далее моделей массового обслуживания дисциплина очереди принимается естественной: первый пришёл, первый обслуживается и она обозначается FCFS. Например, обозначения (Д/Д/1):(FCFS/¥/¥) означают, что мы имеем дело с моделью массового обслуживания, в которой детерминированный входящий поток, один канал обслуживания, естественная дисциплина очереди, неограниченная длина очереди и неограниченная ёмкость источника заявок. Для теории массового обслуживания подобная модель не представляет интереса и здесь рассматриваться не будет. Кроме того, обычно последний блок обозначений считается стандартным и часто не указывается; он подключается в случае, если вводятся ограничения либо на длину очереди, либо на ёмкость источника заявок. Рассмотрим несколько частных стандартных случаев моделей массового обслуживания и приведём формулы для расчёта операционных характеристик таких моделей, имея в виду, что при необходимости эти характеристики могут быть использованы для расчёта стоимостных показателей функционирования систем массового обслуживания и выбора оптимальных стратегий управления этими системами, выбирая уровень обслуживания и издержки системы. Модель 1:(М/М/1) – Одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и экспоненциальным временем обслуживания. Предпосылки модели. Одноканальная однофазная модель массового обслуживания с такими характеристиками является одной из наиболее часто используемых и простых моделей. Она является базовой моделью, поэтому рассмотрим её подробно. Обычно она используется при выполнении следующих семи предпосылок: 1) требования обслуживаются в порядке FCFS; 2) каждое требование дожидается обслуживания, несмотря на длину очереди (система массового обслуживания без отказов); 3) требования поступают в систему независимо друг от друга, случайным образом, с известной (фиксированной в среднем) интенсивностью; 4) закон распределения числа требований, прибывающих в систему за единицу времени, является пуассоновским, и ёмкость источника требований не ограничена (требования поступают из неограниченной совокупности); 5) время обслуживания требований случайное, не меняется от требования к требованию, средняя же интенсивность обслуживания известна; 6) время обслуживания требований подчинено экспоненциальному закону распределения; 7) средняя интенсивность обслуживания больше, чем средняя интенсивность прибытия. Последнее требование обязательно для устойчивого функционирования системы массового обслуживания ибо, в противном случае, очередь будет неограниченно возрастать. Обозначим через l среднее (ожидаемое) число требований за единицу времени, а через m – среднюю интенсивность обслуживания. Тогда, при выполнении перечисленных предпосылок имеем: 1) среднее число требований в системе (в очереди, плюс обслуживаемое) L = l/(m–l); 2) среднее время нахождения требования в системе (время ожидания, плюс время обслуживания) W = 1/(m–l); 3) среднее число требований в очереди Lq = l2 /m (m–l); 4) среднее время ожидания в очереди Wq = l/m (m–l); 5) коэффициент использования времени обслуживания системы, т.е. вероятность того, что система занята обслуживанием r = l/m; 6) вероятность простоя системы массового обслуживания, т.е. вероятность того, что в системе нет ни одного требования Р0 = 1–l/m; 7) вероятность того, что в системе находится n требований Рn = (l/m )n (1–l/m); 8) вероятность того, что в системе находится не менее k требований Рn ³k = (l/m)k . Кроме того, приведём формулы, позволяющие выразить одну из указанных величин через другую, что упрощает иногда их вычисление: Рn = Р0 (l/m)n ; Р0 =1–r ; Lq = L – l/m = l L = Lq + l/m = l W = Wq + 1/l = L /l. Модель 2:(М/GS/1) – одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и произвольным распределением интенсивности обслуживания. В отличие от предыдущей модели здесь предполагается, что закон распределения времени обслуживания неизвестен, но известно среднее время обслуживания (1/m) и его стандартное отклонение s. Тогда характеристика системы определяется из соотношений: Р = l/m; Р0 = 1–l/m; Lq = L = Lq + l/m ; Wq = Lq / l ; W = Wq + 1/ m . Модель 3: (М/D/1) – одноканальная однофазная модель с пуассоновским входящим потоком и фиксированным временем обслуживания. От предыдущей модели эта модель отличается лишь тем, что для неё Модель 4: (М/Еk/1) – одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и выходящим потоком Эрланга (k фаз). Эта модель также является частным случаем модели 2 при s2 =1/km2 . Имеем р=l/m; Р0 = 1–r; Lq = s2 = 1/km2 ; L = Lq +l/m; Wq = Не следует забывать, что, как это было указано при обсуждении закона распределения Эрланга, время обслуживания для каждой фазы считается одинаковым, а общее время обслуживания в системе кратно числу фаз. Например, если время обслуживания для каждой фазы равно 10 минут, а число фаз k=3, то общее время обслуживания равно 30 минут, т.е. интенсивность обслуживания в среднем равна двум требованиям в час (т.е. m=2). Модель 5: (М/М/S) – в отличие от модели 1 здесь предполагается, что система массового обслуживания имеет s каналов обслуживания. Интенсивность каждого канала обслуживания одинакова и равна m, так что суммарная интенсивность системы массового обслуживания равна s Операционные характеристики такой системы определятся из соотношений: Р0 = Рn = Рn = r = L = Lq + l/m ; Wq = Lq /l ; W = Wq + l/m . Модель 6: (M/M/1) : (FCFS /m/¥) От модели 1 эту модель отличает то, что здесь введены ограничения на длину очереди: m – максимальное число требований в системе, следовательно, если в системе заняты все m мест, то очередное требование покинет систему необслуженным. Такая система массового обслуживания называется системой с отказами. Операционные характеристики такой системы определятся из соотношений Р0 = Рm – вероятность того, что требование покинет систему необслуженным. L = Wq = W – Модель 7: (М/М/1):(FCFS/¥/m) В этой модели в отличие от модели 1 предполагается, что ёмкость источника заявок ограничена величиной m. Такие системы массового обслуживания называются замкнутыми. Их операционные характеристики определятся из соотношений Р0 = Lq = m– L = m –
В программе QM в модуле Waiting Lines – линии ожидания или в другой терминологии – система массового обслуживания приводится 9 моделей таких систем в следующих обозначениях:
Вышеописанные модели соответствуют этому списку, кроме модели 7, которая в этом списке обозначена как модель 8. Модели 7 и 8 из этого списка здесь не описаны. Следует отметить, что система МО будет функционировать устойчиво, если интенсивность поступления заявок меньше интенсивности обслуживания. В противном случае очередь будет расти до бесконечности, и в таких ситуациях программа выдаёт предупреждение
- ошибка в данных: интенсивность обслуживания должна быть строго меньше, чем интенсивность прибытия. В таком случае, щёлкнув по кнопке ОК, исправьте данные.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
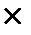 Wq ;
Wq ; ;
; =0.
=0. ;
; ; W = Wq + 1/m.
; W = Wq + 1/m. ;
; , если n £ S ;
, если n £ S ; ;
; ; Lq =
; Lq =  ;
;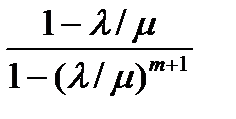 ; Рn = Р0 (l / m)n для n
; Рn = Р0 (l / m)n для n 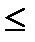 m ;
m ; ; Lq = L –
; Lq = L – 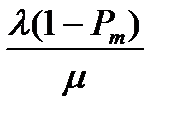 ;
;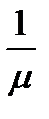 ; W =
; W =  .
. ; Рn =
; Рn =  )
) L = Lq + (1–P0) или
L = Lq + (1–P0) или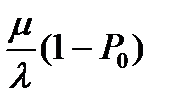 ; Wq =
; Wq =  ; W = Wq + 1/m .
; W = Wq + 1/m .
