
|
|
Двухэтапная транспортная задачаПредположим, что груз непосредственно между поставщиками и потребителями не может. Его сначала нужно завезти на склады, а затем со складов развезти потребителям. В этом случае имеем двухэтапную ТЗ – на первом этапе завезти груз на склады, а на втором – развезти груз со складов потребителям. Не приводя теоретической модели такой задачи, покажем на примере метод её решения. Пусть имеются три поставщика готовой продукции, которую нужно развезти четырём потребителям через два склада. Затраты по перевозке продукции от поставщиков на склады и со складов потребителям составляют
Будем считать, что запасы груза у поставщиков равны соответственно 50, 30 и 20 единиц, вместимость складов – 50 и 60 единиц, а потребности потребителей – 20, 25, 30 и 25 единиц груза. Тогда таблица двухэтапной ТЗ примет вид (рисунок 3.4)
Рисунок 3.4 – Исходная таблица двухэтапной ТЗ
Здесь структура модели следующая. Первый блог коэффициентов (три источника и два пункта назначения – верхние левые три строки и два столбца) – это ТЗ по перевозке груза от поставщиков на склады, следующие 4 столбца (у первых трёх строк) – это как бы поставки груза со складов потребителям, клетки заполнены запретительными тарифами (эти поставки запрещены). Следующие две строки таблицы (Source 4 и Source 5) – это связи складов самих с собой и с потребителями. Первые два столбца – это связи складов самих с собой. Между разными складами связи запрещены – стоят запретительные тарифы, связи складов самих с собой отмечены нулевыми тарифами – поставки не производятся. Это грузы, которые якобы остаются на складах, а на самом деле – мощности складов, не используемые в решении задачи. Диагональ с нулевыми тарифами называется фиктивной. Следующие 4 столбца в этих двух строках – это поставки груза со складов потребителям. Решение данной задачи следующее (рисунок 3.5). Рисунок 3.5 – Решение двухэтапной ТЗ Получили, что от поставщиков на склады груз развезли так: 50 ед. груза от первого поставщика перевезли на первый склад, от 2-го и 3-го поставщиков грузы завезли на второй склад – это 50 ед. груза (30 – от 2-го поставщика и 20 – от 3-го) Второй склад загружен не полностью, что отражено в фиктивной диагонали – 10 ед. груза на пересечении Source 5 и Destination 2 (это связь второго склада самого с собой). В последних двух строках (начиная со столбца Destination 3) отражены перевозки груза со складов потребителям. Суммарная оптимальная стоимость этих перевозок показана в заголовке таблицы – 1050.
Задания к выполнению лабораторной работы №3 вариант 1 вариант 2
вариант 3 вариант 4
вариант 5 вариант 6
вариант 7 вариант 8
вариант 9 вариант 10
вариант 11 вариант 12
вариант 13 вариант 14
вариант 15 вариант 16
вариант 17 вариант 18
вариант 19 вариант 20
Числа в скобках – коэффициенты транспортных расходов, столбец чисел справа от матрицы – запасы груза у поставщиков, строка снизу – потребности потребителей. 1. Решить и проанализировать ТЗ без ограничений. 2. Решить ТЗ с запретом перевозки по самому выгодному пути (с наименьшими затратами). 3. Решить двухэтапную ТЗ с числом поставщиков – 3, складов – 2 и потребителей – 4, взяв за Лабораторная работа №4 Элементы теории игр
Как известно, математика изучает не сами системы, а их модели. В теории игр рассматриваются модели конфликтных ситуаций. Реальные конфликтные ситуации обычно сложны, поэтому исход конфликта зависит от большого количества факторов. Чтобы сделать возможным математический анализ конфликтной ситуации, необходимо создать такую её модель, которая бы учитывала влияние основных факторов и игнорировала второстепенные. Такая упрощённая модель называется игрой. В теории игр используется следующая терминология. Игроки – это стороны, участвующие в конфликте. Игроками могут быть как отдельные личности, так и коллективы людей, имеющие общие цели. Выигрыш (проигрыш) – результат конфликта. Предполагается, что интересы игроков поддаются количественному описанию и, следовательно, выигрыш определяется некоторым числом. В игре могут сталкиваться интересы двух или более игроков. В первом случае игра называется парной, во втором – множественной. Будем рассматривать только парные игры. Игра – совокупность правил, определяющих поведение игроков, партия игры – реализация игры некоторым конкретным образом от начала до конца. Каждая партия игры состоит из последовательности ходов. Ходом в тории игр называется выбор одного из предложенных правилами игры действий и его осуществление. Сами действия называются стратегиями (или чистыми стратегиями). Кроме чистых стратегий существует и понятие смешанных стратегий, в которых чистые стратегии смешиваются определённым образом. Игры бывают одноходовыми и многоходовыми. При одноходовой игре каждый игрок делает по одному ходу и сразу определяется результат игры. Предполагается, что каждому игроку известен набор стратегий противника и результат, к которому приводит выбор определённой стратегии. В сучае двух игроков предполагается, что обе играющие стороны одинаково разумны. От реальной конфликтной ситуации игра отличается тем, что ведётся по определённым правилам, которые известны участникам конфликта и строго ими выполняются. Правила определяют возможные варианты действий участников игры, объём информации об этих действиях, а также результат игры. Целью теории игр является выработка рекомендаций по рациональному образу действий участников многократно повторяющегося конфликта. Каждая стратегия характеризуется величиной проигрыша для одного и соответственно выигрыша для другого игрока. Для разрешения конфликтной ситуации игрокам приходится принимать решения путём выбора той или иной стратегии. Все возможные стратегии обоих игроков и соответствующие им цены Каждый игрок выбирает свою стратегию, не зная, как поступит другой. Поэтому второй игрок, минимизируя свой возможный проигрыш, выбирает ту стратегию, которая минимизирует возможный максимальный проигрыш для каждой стратегии и проигрыш его равен
Первый игрок максимизирует свой гарантированный выигрыш, который соответственно равен
Если a = b = g, то g является ценой игры и в этом случае говорят, что игра имеет седловую точку в чистых стратегиях. Решением игры в этом случае является перечень соответствующих стратегий и цены игры. Покажем это, решив задачу с помощью программы QM в модуле «теория игр». Рассмотрим игру 4х4 с платёжной матрицей А = В диалоговом окне программы QM выберем модуль Game Theory, затем File/New, зададим размерность матрицы 4х4 и введём её в таблицу. Получим после решения задачи (рисунок 4.1)
Рисунок 4.1 – Отчёт о решении задачи На рисунке 4.1 в столбце Row minimum показаны минимальные элементы каждой строки, а в столбце maximin – максимальное из них. Это в наших обозначениях Итак Но подобная ситуация (игра в чистых стратегиях) встречается редко. Чаще встречаются случаи, когда a < b. Тогда говорят, что игра не имеет седловой точки в чистых стратегиях. В этом случае игроки, оптимизируя свои действия, используют несколько своих чистых стратегий, чередуя их случайным образом с некоторыми частотами. Доказано, что любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение, т. е. пару оптимальных стратегий, в общем случае смешанных, и соответствующую цену g (a Обозначим смешанные стратегии игроков через Приведём один из методов решения задачи определения оптимальных смешанных стратегий путём сведения игры к задаче линейного программирования. Обозначим элементы платёжной матрицы через aij и допустим, что все они > 0 и пусть цена игры равна g. Необходимо найти решение игры, т. е. оптимальные смешанные стратегии Найдём оптимальную смешанную стратегию для первого игрока. Применяя свою оптимальную смешанную стратегию, он не может сделать свой выигрыш < g, даже если второй игрок применит любую свою стратегию. Получим
Разделим всё на g и обозначим xi = pi/g. Тогда система неравенств перепишется
Обратите внимание на то, что здесь суммирование производится по i, т.е. коэффициенты строк в этих ограничениях – это столбцы платёжной матрицы. Т.к. åpi = 1, получим åxi = 1/g. Первый игрок максимизирует свой выигрыш, следовательно, 1/g Решение для второго игрока получается как решение задачи, двойственной к составленной. Зная соотношение между решениями исходной и двойственной задач, легко найти решение двойственной по решению исходной, не составляя модель двойственной задачи.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  соответственно
соответственно
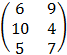 и
и  .
.











 44
44 




















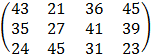












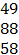
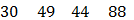


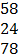










 – последние две строки этой матрицы. Мощности складов одинаковы и равны половине суммарных запасов поставщиков, округлённых до целых десятков в большую сторону.
– последние две строки этой матрицы. Мощности складов одинаковы и равны половине суммарных запасов поставщиков, округлённых до целых десятков в большую сторону. образуют платёжную матрицу. Чистые стратегии первого игрока указываются в строках платёжной матрицы, и предполагается, что этот игрок ориентируется на максимизацию своего гарантированного выигрыша. Чистые стратегии второго игрока отражаются в столбцах этой матрицы, и этот игрок минимизирует свой проигрыш. При этом элемент
образуют платёжную матрицу. Чистые стратегии первого игрока указываются в строках платёжной матрицы, и предполагается, что этот игрок ориентируется на максимизацию своего гарантированного выигрыша. Чистые стратегии второго игрока отражаются в столбцах этой матрицы, и этот игрок минимизирует свой проигрыш. При этом элемент  и
и  (i=
(i=  ), (j=
), (j=  ). Будем рассматривать игру двух лиц с нулевой суммой, когда выигрыш игрока А равен проигрышу игрока В
). Будем рассматривать игру двух лиц с нулевой суммой, когда выигрыш игрока А равен проигрышу игрока В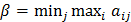 .
. .
. .
.
 – выигрыш игрока А. В строке Column Maximum показаны максимальные значения каждого столбца, а в строке Minimax – минимальное из них.
– выигрыш игрока А. В строке Column Maximum показаны максимальные значения каждого столбца, а в строке Minimax – минимальное из них.  В наших обозначениях это
В наших обозначениях это  .
.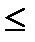 g
g  =(p1, p2, ..., pm) и
=(p1, p2, ..., pm) и  =(q1, q2, ..., qn), где pi – частоты применения первым игроком i-й чистой стратегии (аналог вероятностей), а qj – частоты применения вторым игроком j-й чистой стратегии, причем åpi = 1 и åqj = 1.
=(q1, q2, ..., qn), где pi – частоты применения первым игроком i-й чистой стратегии (аналог вероятностей), а qj – частоты применения вторым игроком j-й чистой стратегии, причем åpi = 1 и åqj = 1.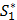 и
и  , дающие каждому игроку оптимальное решение.
, дающие каждому игроку оптимальное решение.
 g, (j=1,2,..,n).
g, (j=1,2,..,n).
 min. Итак, имеем åxi
min. Итак, имеем åxi