
|
|
Бработка резанием как система, управление процессом резания.Целью обраб. мат-лов резанием явл. получ. на заг. новых пов-тей с заданными хар-ми ее кач-ва. Этот рез. достигается путем упругой и пластич. деф-ции срез. слоя и обрабатываемой пов-ти и сопровожд. изнашив. контактных площадок режущего инструмента. Эти пр-сы соверш. одновременно, тесно связаны между собой и образуют единую систему, которая называется системой резания. Система облад. св-вом относит. устойчивости, т. е. она сохраняется только в определенных границах изменения ее переменных. Системе присуще св-во внутренней целостности, которое хар-ся ее автономностью, т.е. относительной самостоятельностью поведения и существования. Вследствие своей относительной автономности любая сист. может рассматрив. как подсистема или эл-т более широкой системы. К входным пар-рам сист. резания относ.: станок (С), приспособление (П), инструмент (И), деталь (Д) или сокращенно СПИД, а также технологическая среда и режим резания, к выходным: точность обработки, кач-во пов-ти, ст-ть ин-та, прочность ин-та, производительность, экономичность. Кроме перечисленных, возможны и другие входные и выходные параметры. М – мат-л, Р – р-р, D - припуск, Fпр и Fpв - функции, связывающие первич. пар-ры с пр-сом резания и пр-с резания со вторич. пар-ми.
В теории автоматического регулирования различают разомкнутые и замкнутые системы. Если изменение выходной величины не вызывает каких-либо изменений входной, система называется разомкнутой. Системы, характеризующиеся замкнутым циклом передачи воздействий, называются замкнутыми. Передача воздействия выходного элемента на входной осуществляется с помощью обратной связи. Если в системе действует одна такая связь, то система называется одноконтурной, а если несколько - многоконтурной. Обработка резанием относ. к объектам многоконтур. рег-ния, поскольку им. большое число регулируемых велич., изменение каждой из которых вызывает измен. других пар-ров. Однако для изуч. свойств отдельных элементов, прежде всего, процесса резания, систему условно можно считать разомкнутой, так как управляющее воздействие на процесс резания и вторичные параметры наступает только со стороны первичных параметров.
17. Основные виды теплообмена и положения учения о теплопроводности. Закон Фурье. Дифференциальное уравнение теплопроводности. Различ. 3 вида теплообмена: теплопроводность, конвекцию и тепловое излучение. Теплопроводность – это пр-с распространения тепловой энергии при непосредственном соприкосновении тел или отдельных частей тела, имеющих разные температуры, например, заготовки, инструмента и деталей технологического оборудования. Конвекция – это процесс перемещения объемов жидкости или газа в пространстве из одной области в другую, отличающихся разной температурой. Тепловое излучение – это процесс распространения тепла в виде электромагнитных волн с взаимным превращением тепловой энергии в лучистую и обратно.
Если температура является функцией трех координат, то температурное поле называется трехмерным, если двух - двухмерным или плоским. Соединив точки в теле с одинаковой температурой, получим изотермические поверхности или поверхности равных температур. Сечение изотермической поверхности плоскостью дает семейство изотермических линий - изотерм. При переходе от одной изотермы к другой температура в теле изменяется, причем наибольший перепад на единицу длины имеет место по направлению нормали к данной изотерме в данной точке. Этот перепад характеризуется величиной
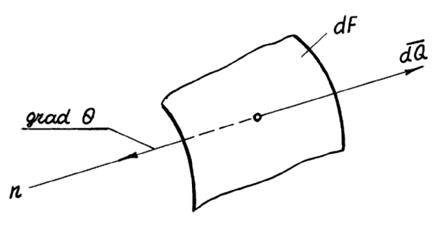
Градиент температуры хар-т интенсивность изменения температуры внутри тела и является векторной величиной, направленной по нормали в сторону возрастания температуры.
Ж.-Б Фурье высказал гипотезу о том, что кол-во теплоты dQ, проходящей через изотермическую поверхность площадью dF за время dt пропорционально градиенту температур:
При нестационарном режиме перераспределение теплоты сопровождается изменением температуры отдельных элементов тела. Изменение температурного поля твердого тела при нестационарной теплопроводности описывается дифференциальным уравнением теплопроводности. Для вывода этого уравнения выделим в теле элементарный объем DxDyDz и рассмотрим процесс распространения теплоты в нем по направлению одной из осей координат, например ОХ.
или
Температура грани ABCD
и тепловой поток
так как
или
Аналогично для координатных осей ОУ и ОZ
Изменение теплового потока во всем теле опишется выражением:
Количество теплоты можно определить также через теплоемкость:
где r- плотность материала; c- массовая теплоемкость; r×c- объемная теплоемкость;
Приравняв выражения, получим диф. уравнение теплопроводности Фурье:
где
18. Схематизация элементов технологической системы с целью описания явления теплопроводности. Метод источников тепла. При решении практических задач, когда имеют дело с конкретными условиями, для описания теплопроводности прибегают к схематизации элементов технологической системы. Схематизация предусматривает рассмотрение частных особенностей, дополняющих и конкретизирующих дифференциальное уравнение теплопроводности применительно к тому или иному случаю, и называемых условиями однозначности или краевыми условиями. Эти условия включают: 1) начальные условия, т. е. распределение температуры в данном теле до того, как начался изучаемый процесс; 2) граничные условия, т. е. описание условий теплообмена поверхностей интересующего нас тела с окружающей средой и другими телами; 3) описание формы, размеров и теплофизических характеристик тела, в котором происходит процесс теплопроводности; 4) описание формы, размеров и мощности источников или стоков тепла, действующих в рассматриваемом процессе ( сток- источник, у которого плотность потока q<0). Схематизация формы тел заключается в представлении их в виде: неограниченного пространства(а) или полупространства (б); неограниченной пластины (в); неограниченного в одном направлении клина (г); неограниченного (д) или ограниченного с одной стороны (е) стержня; тел, имеющих замкнутый объем и простую форму, например, параллелепипеда (ж), шара (з),
Сущность этого метода определяется двумя основными положениями: 1) температурное поле, возникающее в теплопроводном теле под действием источника тепла любой формы, движущегося или неподвижного, действующего временно или непрерывно, можно получить как результат той или иной комбинации температурных полей, возникающих под действием системы точечных мгновенных источников; 2) процесс распространения теплоты в теле представляется в виде части распространения теплоты в теле неограниченных размеров путем дополнения к фактически действующим источникам некоторой системы фиктивных источников или стоков теплоты. Если предположить, что в теле, все точки которого имеют одинаковую температуру, а теплообмен с окружающей средой отсутствует, вспыхнул и мгновенно погас точечный источник, выделивший qT тепла, то решение дифференциального уравнения теплопроводности для этих условий запишется в виде:
где qт(x, y, z, t)- температура любой точки тела; x, y, z- координаты точки тела; xи, yи, zи- координаты источника тепла; t- время действия источника; l и w- коэффициенты соответственно теплопроводности и температуропроводности материала тела. Решения дифференциального уравнения для других условий получаются путем интерпретации формы, времени и движения источников теплоты. Например, источник в виде прямой линии может быть представлен как совокупность бесконечно большого числа точечных, поставленных рядом и действующих одновременно. Если источник действует в течение времени t, то его можно представить в виде системы мгновенных точечных источников, вспыхивающих и гаснущих с весьма большой частотой, когда период времени между вспышкой и гашением Движение источника можно имитировать рядом последовательных вспышек и гашений мгновенных импульсов в различных точках траекторий перемещения источника. Это легко уяснить, если представить, что ряд последовательно зажигающихся и гаснущих лампочек создают иллюзию движения светового луча. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
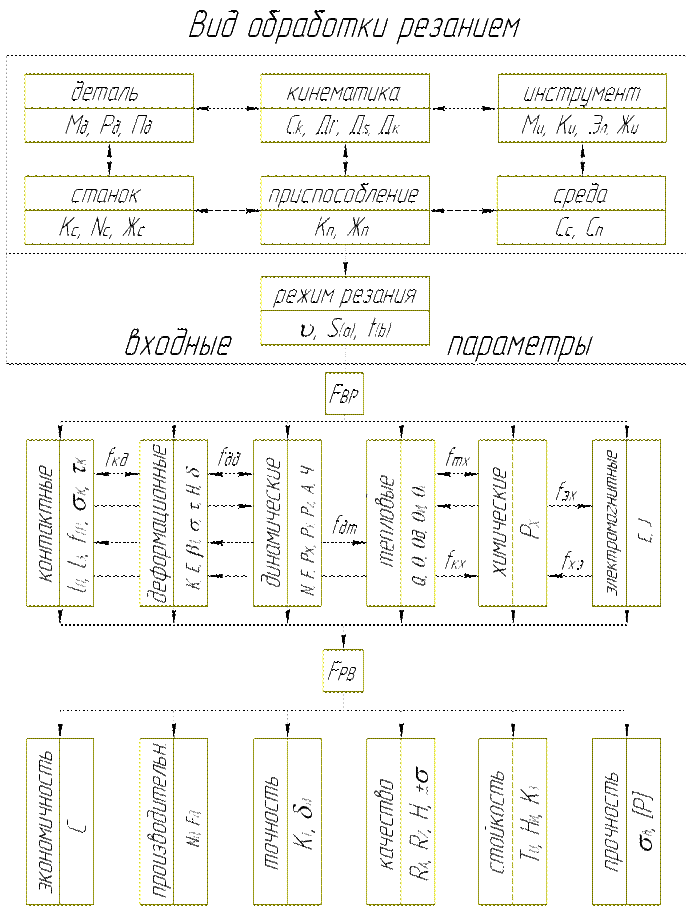 Пр-с резания представл. собой слож. комплекс физико-хим. явл. Условия протекания процесса резания определяются кинематической схемой резания, упругими и пластическими деформациями обрабатываемого материала, его разрушением в зоне резания, трением, тепловыми явлениями, химическими, электрическими и магнитными явлениями, а также другими факторами. В соответствии с этим систему резания можно разделить на ряд частных подсистем: механическую, тепловую и т. п. Следует отметить, что все подсистемы являются замкнутыми системами, в которых выход последнего элемента связан с входом в первый. Закономерности функционирования таких систем рассматривает теория автоматического регулирования.
Пр-с резания представл. собой слож. комплекс физико-хим. явл. Условия протекания процесса резания определяются кинематической схемой резания, упругими и пластическими деформациями обрабатываемого материала, его разрушением в зоне резания, трением, тепловыми явлениями, химическими, электрическими и магнитными явлениями, а также другими факторами. В соответствии с этим систему резания можно разделить на ряд частных подсистем: механическую, тепловую и т. п. Следует отметить, что все подсистемы являются замкнутыми системами, в которых выход последнего элемента связан с входом в первый. Закономерности функционирования таких систем рассматривает теория автоматического регулирования. Объектом регулирования по этой схеме являются все первичные параметры и, в первую очередь, в качестве регулятора используют изменение режимов резания (Рж). Регулирования процесса обработки в этом случае заключается в том, чтобы, исходя из знания параметров детали, вида обработки и технологической среды путем изменения режима резания получить необходимые параметры функционирования системы. Взаимодействие регулятора с элементами системы осуществляется путем обратных связей 1–7, например, подача S определяет свойства динамической системы (связь 1), которые в свою очередь зависят от конструкции приспособления П и инструмента И (связь 6 и 5). Скорость резания υ определяет главным образом тепловые явления (связь 2), а кинематика процесса резания влияет на пластические дефрмации и трение (связь 3) и точность обработки Тч (связь 7). В качестве регултора при этом чаще всего используется подача S (связь 4). В конечном итоге регулирование свойств подсистем и процесса резания определяет выходные параметры – точность Тч, качество поверхности Кп, стойкость Си и прочность Пи инструмента, производительность Пр и экономичность Эк обработки.
Объектом регулирования по этой схеме являются все первичные параметры и, в первую очередь, в качестве регулятора используют изменение режимов резания (Рж). Регулирования процесса обработки в этом случае заключается в том, чтобы, исходя из знания параметров детали, вида обработки и технологической среды путем изменения режима резания получить необходимые параметры функционирования системы. Взаимодействие регулятора с элементами системы осуществляется путем обратных связей 1–7, например, подача S определяет свойства динамической системы (связь 1), которые в свою очередь зависят от конструкции приспособления П и инструмента И (связь 6 и 5). Скорость резания υ определяет главным образом тепловые явления (связь 2), а кинематика процесса резания влияет на пластические дефрмации и трение (связь 3) и точность обработки Тч (связь 7). В качестве регултора при этом чаще всего используется подача S (связь 4). В конечном итоге регулирование свойств подсистем и процесса резания определяет выходные параметры – точность Тч, качество поверхности Кп, стойкость Си и прочность Пи инструмента, производительность Пр и экономичность Эк обработки.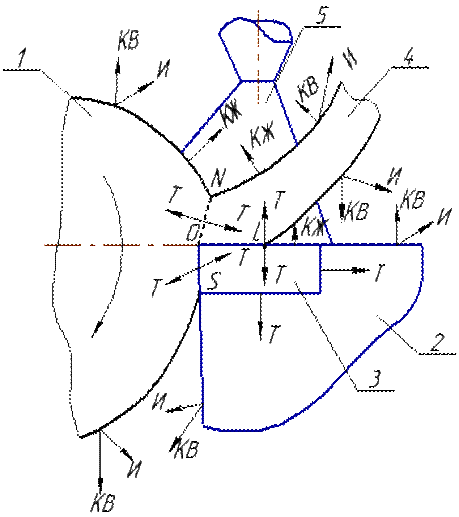 В твердых телах эн-ю частиц в-ва хар-т такой парр, как температура. Если в твердом теле распространяется тепло, то температура в различных точках тела с координатами (x, y, z) и в разное время t описывается выражением q = f(x, y, z, t). Совокупность значений температур в различных точках тела в данный момент времени называется температурным полем.
В твердых телах эн-ю частиц в-ва хар-т такой парр, как температура. Если в твердом теле распространяется тепло, то температура в различных точках тела с координатами (x, y, z) и в разное время t описывается выражением q = f(x, y, z, t). Совокупность значений температур в различных точках тела в данный момент времени называется температурным полем.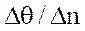 , а предел этого отношения
, а предел этого отношения  называется градиентом температуры:
называется градиентом температуры:
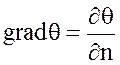
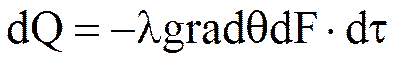 .
.
 За малостью площади DyDz положим, что температура на каждой грани тела расп-на равномерно. Пусть на грани A1B1C1D1 температура равна q, а на грани ABCD- q/ =q+Dqx, где Dqx - изменение температуры вдоль оси ОХ. Изменение теплового потока от одной грани к другой по направлению ОХ рассматриваемого тела опишется выражением:
За малостью площади DyDz положим, что температура на каждой грани тела расп-на равномерно. Пусть на грани A1B1C1D1 температура равна q, а на грани ABCD- q/ =q+Dqx, где Dqx - изменение температуры вдоль оси ОХ. Изменение теплового потока от одной грани к другой по направлению ОХ рассматриваемого тела опишется выражением: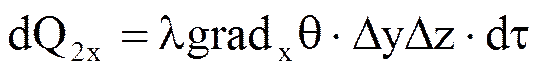
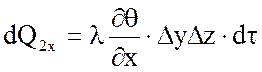 .
. , тогда
, тогда ,
,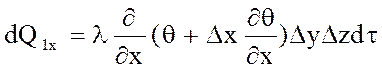 ,
, , то в объеме
, то в объеме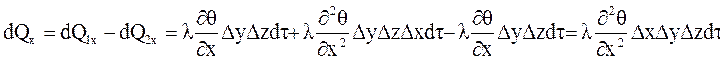
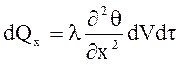
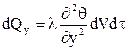 ,
,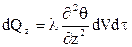 .
.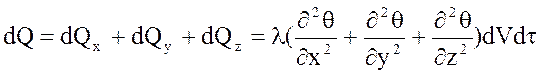 .
.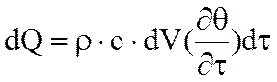 ,
,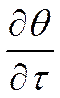 - скорость изменения температуры тела во времени.
- скорость изменения температуры тела во времени. ,
,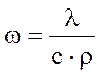 - коэф. температуропроводности, характеризующий теплоинерционные свойства тела.
- коэф. температуропроводности, характеризующий теплоинерционные свойства тела.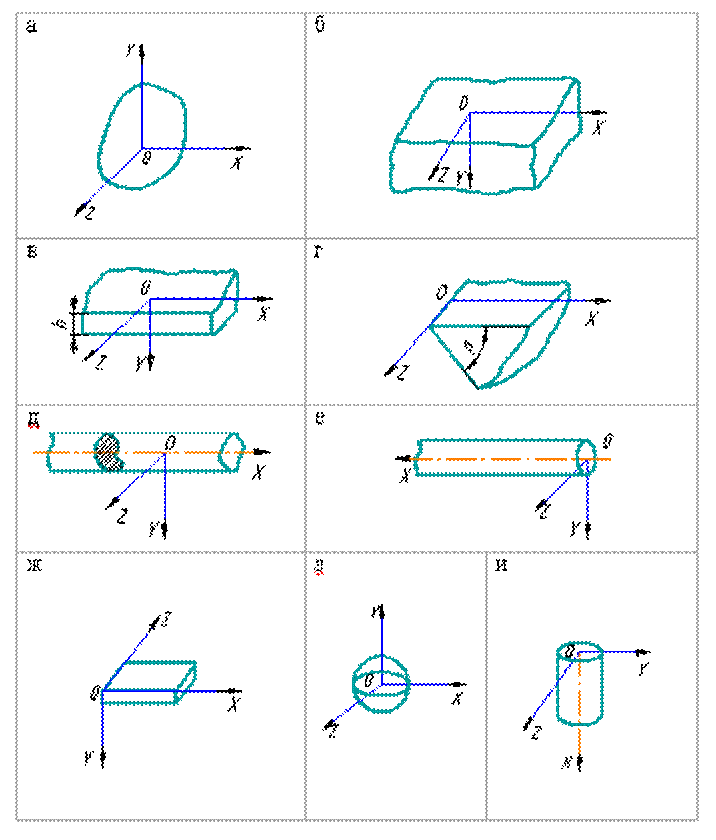 цилиндра (и). Источники теплоты схематизируются: по форме и могут быть трех-, двух- и одномерные, а также точечные; по скорости перемещения- неподвижные, движущиеся, быстродвижущиеся; по времени функционирования- мгновенные, действующие в течение конечного отрезка времени, действующие периодически и стационарные.
цилиндра (и). Источники теплоты схематизируются: по форме и могут быть трех-, двух- и одномерные, а также точечные; по скорости перемещения- неподвижные, движущиеся, быстродвижущиеся; по времени функционирования- мгновенные, действующие в течение конечного отрезка времени, действующие периодически и стационарные.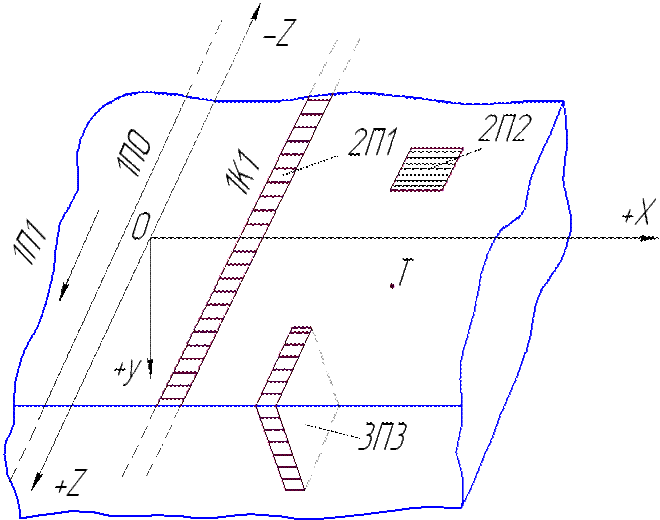
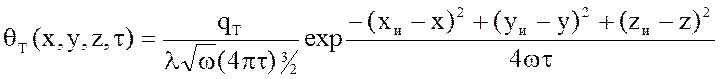
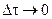 . В этом случае импульсы следуют друг за другом с бесконечно малыми промежутками времени и в пределе образуется непрерывно функционирующий источник.
. В этом случае импульсы следуют друг за другом с бесконечно малыми промежутками времени и в пределе образуется непрерывно функционирующий источник.