
|
|
Решение системы нелинейных уравнений методом НьютонаРассмотрим систему n нелинейных уравнений с n неизвестными:
или в виде вектор – функции Разложим левые части уравнений в ряд Тейлора в окрестности точки
Введем в рассмотрение вектора и матрицы:
Тогда полученное разложение можно записать компактно в матричной форме:
Матрица Линеаризация уравнений в окрестности точки Пример: Для решения системы УУН, соответствующей рис. 6.2 методом Ньютона выполнить одну итерацию.
Матрица Якоби имеет вид:
В качестве начальных приближений примем напряжения узлов равными напряжению базисного узла Вектор функций невязок мощности в узлах
Матрица Якоби
Для получения первого приближения
Для выполнения второй итерации нужно вычислить вектор
и вновь решить систему уравнений относительно вектора 6.2. Методы простой итерации и Зейделя-Гаусса Рассмотрим нелинейное уравнение Ход итерационного процесса можно проследить графически, построив отдельно левую и правую части рекуррентного соотношения. Для произвольно взятого х0 проводится вертикаль до пересечения с Возможны следующие реализации итерационного процесса: монотонная сходимость,
Рис. 6.3. Метод постой итерации, монотонный процесс : а)
Рис. 6.4. Метод постой итерации, колебательный процесс : а) Критерий сходимости метода простой итерации Для того чтобы итерационный процесс метода простой итерации сходился достаточно, чтобы для всех Для доказательства этого запишем рекуррентные выражения двух соседних итераций
Разложим функцию j в окрестности
Отсюда
Для обеспечения сходимости необходимо, чтобы Приведенный анализ показывает основные проблемы итерационных процессов, присущих не только методу простой итерации, но и всем остальным итерационным методам: сходимость или расходимость процесса, критерий и характер сходимости (монотонная, колебательная). Расходящийся итерационный процесс еще не говорит об отсутствии решения. Решение может быть найдено использованием иного математического метода или иной структурой рекуррентного соотношения.
Выражая из первого слагаемого переменную х, получим соотношение: Примем начальное приближение
После семи итераций получается точное решение Легко проверить, что критерий сходимости выполняется, как в точке начального приближения, так и для всех Следует отметить, что рассматриваемое уравнение имеет еще один корень

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , ограничившись производными первого порядка.
, ограничившись производными первого порядка.

 , где
, где 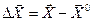 .
. получила название матрицы Якоби. Элемент матрицы Якоби, стоящий на пересечении i-ой строки и j- столбца равен производной от i-го уравнения по j-ой переменной
получила название матрицы Якоби. Элемент матрицы Якоби, стоящий на пересечении i-ой строки и j- столбца равен производной от i-го уравнения по j-ой переменной  . Матрица Якоби является аналогом производной вектор – функции.
. Матрица Якоби является аналогом производной вектор – функции. ,
,  .
.
 .
.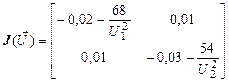 .
. .
.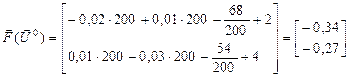 .
.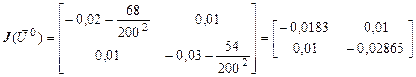
 решается система линейных уравнений:
решается система линейных уравнений: , откуда
, откуда и
и  ;
;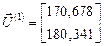 .
. =(-0,0086; -0,0029)t, найти значения матрицы Якоби
=(-0,0086; -0,0029)t, найти значения матрицы Якоби =
= 
 . Здесь
. Здесь  . В результате второй итерации будет получено практически точное решение
. В результате второй итерации будет получено практически точное решение  и
и  .
. с одной переменной. Для получения рекуррентного соотношения простой итерации его нужно преобразовать к виду
с одной переменной. Для получения рекуррентного соотношения простой итерации его нужно преобразовать к виду  .
. . Значение
. Значение 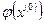 будет принято в качестве х1 . Поскольку функция y=x имеет угол наклона равный 450, то х1 находится как абсцисса точки пересечения горизонтали
будет принято в качестве х1 . Поскольку функция y=x имеет угол наклона равный 450, то х1 находится как абсцисса точки пересечения горизонтали  , рис. 6.3, а; монотонная расходимость,
, рис. 6.3, а; монотонная расходимость, 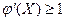 , рис. 6.3, b, колебательная сходимость; рис. 6.4, а; колебательная расходимость, рис. 6.4, b.
, рис. 6.3, b, колебательная сходимость; рис. 6.4, а; колебательная расходимость, рис. 6.4, b.



 ; b)
; b) 
 выполнялось условие
выполнялось условие  , которое можно рассматривать как критериальное.
, которое можно рассматривать как критериальное. . Отсюда
. Отсюда .
. в ряд Тейлора:
в ряд Тейлора: .
.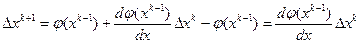 .
. . Это возможно лишь в том случае, когда
. Это возможно лишь в том случае, когда  , что и требовалось доказать.
, что и требовалось доказать. Пример. Рассмотрим уравнение УУН. соответствующее рис. 6.5
Пример. Рассмотрим уравнение УУН. соответствующее рис. 6.5  .
. , которое легко представить в виде рекуррентного выражения:
, которое легко представить в виде рекуррентного выражения: 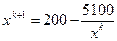 .
. . Тогда:
. Тогда: .
. .
. , k=1,2,…, т.к.
, k=1,2,…, т.к.  при всех x>71,41.
при всех x>71,41. , но получить это решение по представленному рекуррентному соотношению не удается, даже если взять начальное приближение в непосредственной близости от
, но получить это решение по представленному рекуррентному соотношению не удается, даже если взять начальное приближение в непосредственной близости от  и выразить из этого уравнения
и выразить из этого уравнения  , то соответствующее рекуррентное соотношение
, то соответствующее рекуррентное соотношение  обеспечивает сходимость к корню
обеспечивает сходимость к корню