
|
|
Размерность линейного пространстваПусть R – линейное пространство. Вектора
справедливо лишь в том случае, когда все a1,a2,…,an, равны нулю. Если в (7.1 ) хотя бы один коэффициент не равен нулю, то вектора являются линейно-зависимыми и при этом существует хотя бы один вектор, который может быть выражен через другие:
Линейное пространство называется n-мерным (Rn), если в нем существует n линейно независимых векторов и любые n+1 векторов связаны линейной зависимостью. Например, в R2 третий вектор
Базис и координаты в n-мерном пространстве Совокупность каких-либо n линейно независимых векторов Любой вектор
Числа xi называются координатами вектора Используя частный случай единичных базисных векторов
можно любой набор n чисел (x1, x2 …xn) представить вектором
т.е. координаты суммы векторов равны сумме соответствующих координат. Понятие базиса и координат вектора Х произвольной природы в базисе
можно представить через базис
в котором
Евклидово пространство Линейное пространство Rnвекторов над полем Р вещественных чисел называется евклидовым, если в нем определена операция скалярного произведения, где каждой паре векторов
Ортонормированный базис это базис { В ортонормированном базисе координаты вектора могут быть выражены через скалярное произведение В ортонормированном и только в ортонормированном базисе евклидового пространства для векторов – столбцов чисел – скалярное произведение может быть определено как По аналогии с трехмерным пространством можно определить понятие длины или модуля вектора:
Скалярное произведение в произвольном базисе
Пример. Пусть
В результате
В пространстве С[a,b] функций, определенных на отрезке [a,b] скалярное произведение
Из соотношений, характеризующих скалярное произведение векторов в пространстве непрерывных функций, следуют очень полезные в практических приложениях для предельных оценок Неравенство Коши-Буняковского
Неравенство треугольника (Минковского)
Линейные преобразования В линейном пространстве можно ввести функцию, ставящую в соответствие любому вектору
где Вектор
Преобразование называется линейным, если 1) 2) Пусть Если Используя свойства линейного преобразования, получаем:
Если образы векторов базиса известны, то можно записать:
поскольку
Отсюда В результате Пример. Линейное преобразование задано матрицей Решение Определить прообраз вектора Решение. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,i =1,…,n называются линейно – независимыми, если выражение:
,i =1,…,n называются линейно – независимыми, если выражение:

 является линейной комбинацией линейно-независимых векторов
является линейной комбинацией линейно-независимых векторов  :
:  .
. называются базисом n-мерного пространства.
называются базисом n-мерного пространства.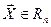 может быть представлен в виде линейной комбинации базисных векторов
может быть представлен в виде линейной комбинации базисных векторов  .
. в базисе
в базисе 
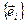 .
.  Если при этом
Если при этом  , то
, то ,
,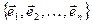 позволяет свести вектора любого характера к векторам, представляющим собой систему n чисел. Например, многочлены
позволяет свести вектора любого характера к векторам, представляющим собой систему n чисел. Например, многочлены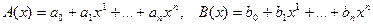
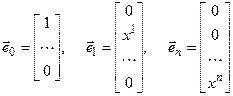 ,
, , т.е. множество полиномов степениn представляется как линейное пространство Rn+1. Этот результат справедлив для любых векторов и в общем виде сводится к алгебраической неразличимости (изоморфизму) векторов любой природы, но одинаковой размерности.
, т.е. множество полиномов степениn представляется как линейное пространство Rn+1. Этот результат справедлив для любых векторов и в общем виде сводится к алгебраической неразличимости (изоморфизму) векторов любой природы, но одинаковой размерности. и обладающее следующими свойствами:
и обладающее следующими свойствами:
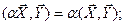

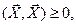 и
и 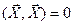 только если
только если  .
. , i=1,…,n}, где (
, i=1,…,n}, где ( 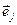 )=0; (
)=0; (  , т.е. xi является проекцией вектора
, т.е. xi является проекцией вектора  , поскольку в силу ортонормированности
, поскольку в силу ортонормированности 
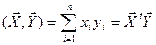 , где
, где  -вектор строка.
-вектор строка. , и угла между векторами:
, и угла между векторами: 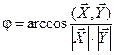 .
. представляется более сложной функциональной зависимостью
представляется более сложной функциональной зависимостью , где
, где 
 , (рис. 7.2).
, (рис. 7.2). Матрица коэффициентов
Матрица коэффициентов
 .
.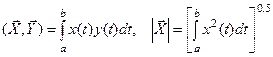 .
. ;
; .
. того же пространства:
того же пространства: ,
, – функция преобразования пространства. Обозначение
– функция преобразования пространства. Обозначение  - называется оператором. Если вектор
- называется оператором. Если вектор 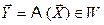 , то говорят о преобразовании пространств V®W. Если пространство преобразуется в себя V®V, то это линейное преобразование.
, то говорят о преобразовании пространств V®W. Если пространство преобразуется в себя V®V, то это линейное преобразование.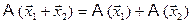 ;
; .
. Покажем, что это так.
Покажем, что это так.

 ,
, , как любой произвольный вектор, имеет разложение в существующем базисе. Тогда
, как любой произвольный вектор, имеет разложение в существующем базисе. Тогда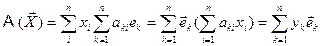 .
.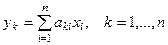 .
. , где матрица А линейного преобразования есть матрица, столбцами которой являются образы базисных векторов. Таким образом, любые линейные преобразования можно описывать с помощью матриц и каждая матрица представляет некоторое линейное преобразование.
, где матрица А линейного преобразования есть матрица, столбцами которой являются образы базисных векторов. Таким образом, любые линейные преобразования можно описывать с помощью матриц и каждая матрица представляет некоторое линейное преобразование. . Определить образ вектора
. Определить образ вектора  .
.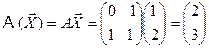 .
. .
. .
.