
|
|
Дифференциальные уравнения первого порядкаДифференциальное уравнение первого порядка имеет вид
или
Дифференциальные уравнения классифицируются как · Линейные, например · нелинейные, например В свою очередь линейные ДУ делятся на · однородные · неоднородные Если ДУ первого порядка
Для непрерывных в некоторой области функций Существует частное решение
Числа Линейное однородное дифференциальное уравнение первого порядка имеет вид
. Относительно производной
Общее решение этого уравнения с разделяющимися переменными
где С - произвольное действительное число.
Пример. Найти общее и частное решение дифференциального уравнения Преобразуем уравнение к виду (7.10):
Общее решение По условию известно, что при Аналитический метод решения систем линейных однородных дифференциальных уравнений Рассматривается система линейных однородных дифференциальных уравнений (СЛДУ) первого порядка
Система (7.14), когда в левой части уравнений стоят производные, а правая часть производных не содержит, называется нормальной. Путем замены переменных (например, В матричной форме записи система (7.14) может быть представлена уравнением:
где
Пример. Привести к нормальной форме записи уравнение вида
Выполним замену переменных
Эта система может быть представлена в виде, приемлемом для матричной формы
Принимая во внимание, что любая матрица является отражением линейного преобразования, можно заметить, что система ДУ ставит в соответствие вектору переменных вектор производных (образ исходного вектора), В разделе 7.5 было сказано, что существует такой базис (система собственных векторов
или в матричной форме
где
Учитывая преобразования перехода к старому базису, получаем
где Н - матрица, состоящая из собственных векторов При t=0 матрица
Окончательно, решение СЛДУ
Пример. Найти решение системы линейных однородных дифференциальных уравнений
с начальными условиями Матрица А имеет вид:
Найдем корни характеристического уравнения Определим собственные вектора. Для
Строки полученной матрицы являются линейно-зависимыми. Решим систему уравнений для определения первого собственного вектора
при Аналогично определим второй собственный вектор Матрица
Решение рассматриваемой системы дифференциальных уравнений получается в виде (7.18),
или 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
. ;
; .
. ;
; , где
, где 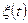 - произвольная непрерывная функция времени. Если
- произвольная непрерывная функция времени. Если  , уравнение становится однородным.
, уравнение становится однородным. , то, как правило, оно представляется в виде
, то, как правило, оно представляется в виде .
.
 и
и  уравнение (7.10) имеет бесконечное множество решений. Общим решением уравнения (7.10) является некоторая функция
уравнение (7.10) имеет бесконечное множество решений. Общим решением уравнения (7.10) является некоторая функция 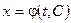 .
. уравнения (7.10), удовлетворяющее условию
уравнения (7.10), удовлетворяющее условию .
.
 называются начальными значениями для решения
называются начальными значениями для решения  , называется частным решением ДУ.
, называется частным решением ДУ.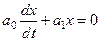 .
.
 уравнение (7.12) преобразуется к виду
уравнение (7.12) преобразуется к виду
 .
. ,
,
 Геометрически на плоскости общее решение ДУ (рис. 7.10) представляется семейством кривых, каждая из которых соответствует различным начальным условиям.
Геометрически на плоскости общее решение ДУ (рис. 7.10) представляется семейством кривых, каждая из которых соответствует различным начальным условиям. при заданных начальных значениях
при заданных начальных значениях  ,
,  .
.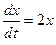 .
.
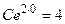 , откуда
, откуда  . Частное решение исходного ДУ
. Частное решение исходного ДУ  .
. .
.
 ) к нормальному виду может быть приведена любая нелинейная система ДУ с производными высших порядков.
) к нормальному виду может быть приведена любая нелинейная система ДУ с производными высших порядков. ,
,
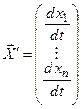 ;
;  ;
;  .
. .
. ,
, 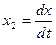 , тогда исходное ДУ преобразуется в систему
, тогда исходное ДУ преобразуется в систему

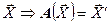 . Далее этот тезис будет расширен.
. Далее этот тезис будет расширен.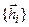 ), где матрица линейного преобразования является диагональной
), где матрица линейного преобразования является диагональной  . В базисе
. В базисе 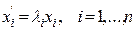 . Нетрудно получить решение представленных ДУ. Оно имеет вид
. Нетрудно получить решение представленных ДУ. Оно имеет вид ,
,
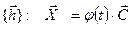 ,
, - функциональная матрица (квадратная, порядка n), диагональными элементами которой являются экспоненциальные функции
- функциональная матрица (квадратная, порядка n), диагональными элементами которой являются экспоненциальные функции 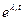 ,
,  , а недиагональные элементы равны нулю.
, а недиагональные элементы равны нулю. .
. ,
,
 .
.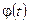 преобразуется в единичную, В результате получаем
преобразуется в единичную, В результате получаем .
.

 ,
, 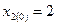 ,.
,. . Для нахождения собственных чисел составим характеристический определитель
. Для нахождения собственных чисел составим характеристический определитель .
. , которые одновременно являются собственными числами матрицы А:
, которые одновременно являются собственными числами матрицы А:  и
и  .
. .
.
 получим значение
получим значение 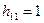 , тогда
, тогда  .
. .
. имеет вид
имеет вид  , а обратная к ней
, а обратная к ней .
.
 .
.