
|
|
Элементарные операции с матрицамиДве матрицы считаются равными тогда и только тогда, когда они имеют одинаковые размерности и соответствующие элементы,
Сложение двух матриц A и B: C = A + B Операция сложения матриц обладает переместительным и сочетательным свойствами: А + В = В+ А; (А + В) + С = А + (В + С). Здесь А, В, С произвольные прямоугольные матрицы одинакового размера. Умножение матрицы на число: B = aA, a(A + B) = aA + aB; (a + b)A = aA+bA (ab)A = a(bA) Произведение двух матриц А и В:
Эта операция возможна при условии, что количество столбцов матрицыAравно количеству строк матрицы В. Матрица - произведение С имеет столько же столбцов, сколько их у матрицы B, и столько же строк, сколько их у матрицы A. Элемент сij - есть скалярное произведение i - той строки матрицы А и j - ого столбца матрицы B: сij.= Для умножения матриц справедливо сочетательное свойство, а также распределительное свойство умножения относительно сложения: (АВ) С = А (ВС); (А + В)С = АС + ВС; А(В + С) = АВ+АС. Умножение матриц не обладает переместительным свойством: АВ ¹ВА (Если АВ=ВА, то матрицы А и Вназываются перестановочными или коммутирующими между собой). Определитель матрицы Одной из числовых характеристик квадратной матрицы является ее определитель. Для вычисления определителя второго и третьего порядка обычно используют правило Саррюса (схема диагоналей и треугольников), согласно которому
Первое слагаемое, входящих в правую часть со знаком плюс, есть произведение элементов главнойдиагонали матрицы А, следующие два — произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла матрицы. Слагаемые, входящие в (3.1) со знаком минус, строятся таким же образом, но относительно побочной диагонали. Данному правилу соответствуют схемы, облегчающие вычисление слагаемых:
Для определителя второго порядка
Однако чаще всего определитель вычисляется по формуле разложения по строке или столбцу. При этом необходимо ввести некоторые понятия. Минором Алгебраическим дополнением
Определитель равен сумме произведений элементов какой - либо его строки (какого - либо столбца) на соответствующие алгебраические дополнения элементов этой строки (этого столбца).
где
Свойства определителей 1. Равноправность строк и столбцов. Все свойства определителей, сформулированные для строк, справедливы и для столбцов. 2. Величина определителя не меняется при транспонировании матрицы. 3. При перестановке местами двух строк (или столбцов) определитель меняет знак, сохраняя абсолютную величину. 4. Определитель, содержащий две одинаковые строки (или столбца), равен нулю. 5. Общий множитель всех элементов некоторой строки (или столбца) определителя можно выносить за знак этого определителя. 6. Если все элементы некоторой стоки (или некоторого столбца) определителя равны нулю, то и сам определитель равен нулю. 7. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю. 8. Если к элементам некоторой строки (или столбца) определителя прибавить умноженные на произвольный множитель соответствующие элементы другой строки (другого столбца), то величина определителя не изменится. 9. Скалярное произведение элементов строки i матрицы А на алгебраические дополнения любой другой строки равно нулю, Читателю предлагается самостоятельно доказать свойства 4-9. Ранг матрицы Квадратная матрица называется невырожденной (неособенной) если ее определитель не равен нулю. Матрица имеет ранг rang(A)= ρ, если А имеет по меньшей мере одну невырожденную подматрицу порядка ρ, а все квадратные подматрицы порядка выше ρ являются вырожденными. Иначе, ранг матрицы – наибольший порядок невырожденных квадратных подматриц. Если рассматривать строки (столбцы) матрицы как вектора, то ранг матрицы А равен максимальному числу линейно независимых строк (столбцов) матрицы. Ранг матрицы не изменяется при: · перемене мест строк (столбцов) матрицы; · умножении строки (столбца) на скаляр λ≠0; · транспонировании матрицы; 3.2. Обратная матрица Произвольная квадратная матрица А, определитель которой отличен от нуля, обладает обратной матрицей А-1. При этом А А-1= А-1 А =Е. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. сij = aij + bij, i =1,...,n, j=1,...,m, dim A=dim B=dim С.
сij = aij + bij, i =1,...,n, j=1,...,m, dim A=dim B=dim С. i =1,...,n, j=1,...,s, dim A=n,m, dim B=m,s, dim C=n,s .
i =1,...,n, j=1,...,s, dim A=n,m, dim B=m,s, dim C=n,s . .
.


 .
. . Пример.
. Пример. 
 элемента
элемента  определителя порядка n называется определитель порядка
определителя порядка n называется определитель порядка  , получаемый из исходного определителя путем вычеркивания строки i и столбца j, на пересечении которых стоит указанный элемент
, получаемый из исходного определителя путем вычеркивания строки i и столбца j, на пересечении которых стоит указанный элемент  элемента
элемента 
 ,
, - элементы строки i;
- элементы строки i;  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 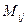 - минор – определитель матрицы, полученной из исходной вычеркиванием строки i и столбца j. В частности, для определителя третьего порядка
- минор – определитель матрицы, полученной из исходной вычеркиванием строки i и столбца j. В частности, для определителя третьего порядка
 .
.