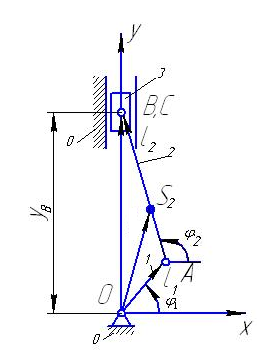
Графический метод решения

3.4.1.1 Построение плана положений механизма

Рассчитав значения l_OA, l_AB, l_AS₂ можно приступить к построению плана положений механизма.

Так как данный механизм имеет вертикальное расположение, то геометрическое место точек всех положений ползуна находится на вертикальной прямой, проходящей через ось вращения кривошипа.

Для построения плана положений механизма необходимо задать масштабный коэффициент, с помощью которого реальные размеры звеньев механизма выражаются в отрезках, изображаемых на чертеже.

Принимаем

Определим значения величин AB и AS₂:

На листе формата А1 выбираем точку O и наносим систему координат XOY. Из точки O проводим окружность радиуса OА и разбиваем ее на 12 равных частей. Полученные на окружности точки нумеруем от «1» до «13» (начинаем с верхней, и далее по ходу вращения кривошипа) и соединяем их с центром О. Данные отрезки будут являться положениями кривошипа.

Из точек на окружности проводим отрезки длиной АВ до пересечения их с осью OY и полученные на оси ординат точки нумеруем в соответствии с нумерацией точек на окружности. Данные точки будут являться планом положений ползуна, а отрезки - шатуна.

На плане положений шатуна от точек Ai откладываем отрезки длиной AS₂, и полученные точки нумеруем соответственно.

- начальная обобщенная координата, соответствующая положению механизма в верхней мертвой точке.

3.4.1.2 Построение плана аналогов скоростей и определение первых передаточных функций механизма

Используя соотношение _э строим план аналогов скоростей.

- аналог скорости.

Для построения плана аналогов скоростей выбираем контрольное положение, при котором = 30°.

Примем масштабный коэффициент плана аналогов скоростей

Строим на чертеже точку р - полюс плана аналогов скоростей. Проводим из точки р отрезок рa перпендикулярный OА и направленный в сторону вращения кривошипа (аналог скорости совпадает по направлению с вектором скорости).

Аналог скорости точки A – отрезок рa =OА=50мм.

Для точки B записываем систему векторных уравнений:

, (3.2)

где

Так как то точка b₀ совпадает с полюсом плана аналогов скоростей p.

Из точки a строим прямую линию перпендикулярную шатуну AВ плана положений механизма. Из точки p строим прямую линию параллельную оси ОY плана положений механизма. На пересечении этих линий получаем точку b.

Точку s₂ на плане строим исходя из теоремы подобия:

, для 3-го положения

, для 9-го положения

где ab – отрезок на плане аналогов скоростей.

Определив расположение точки s₂на плане аналогов скоростей, определяем величины ps₂, x_s₂ и y_s₂.

Определим первые передаточные функции графическим способом:

для 3-го положения

для 9-го положения

Сведем значение величин, полученных графическим методом в таблицу 3.2 .

Таблица 3.2 – Результаты построений и вычислений

№ п/п	Отрезки, мм	Результаты вычислений, м
pa	pb	ab	ps₂	as₂	x_s2	y_s2	i₃₁	i_s21	i₂₁	x´_s2	y´_s2
			44,0	28,6				0,000	0,057	0,251	0,056	0,000
			39,0	35,0				0,056	0,070	0,223	0,048	0,048
			23,0	42,0				0,086	0,084	0,131	0,028	0,080
			0,0	44,0				0,088	0,088	0,000	0,000	0,088
			22,0	39,0				0,066	0,078	0,126	0,028	0,072
			39,0	32,0				0,034	0,064	0,223	0,048	0,040
			44,0	28,6				0,000	0,057	0,251	0,056	0,000
			38,0	32,0				0,036	0,064	0,217	0,050	0,040
			22,5	38,0				0,066	0,076	0,129	0,028	0,072
			0,0	44,0				0,088	0,088	0,000	0,000	0,088
			23,0	42,0				0,086	0,084	0,131	0,028	0,080
			38,0	34,0				0,056	0,068	0,217	0,050	0,048

Аналитический метод решения

Составление схемы алгоритма расчета кинематических

Характеристик механизма

Рисунок 3.4. Расчетная схема механизма

Алгоритм вычислений кинематических характеристик механизма имеет вид (Методическое пособие «Динамика машин и механизмов в установившемся режиме движения»):

10.

11.

12.

13.

14.

15.

16.

17.

Примечание: 1. В формуле (3) a=+1, если ползун расположен сверху от начала координат, a=–1, если ползун расположен снизу.

Расчет кинематических характеристик рычажного механизма

Алгоритм вычислений полученный в пункте 3.4.2.1. используем для контрольного положения механизма с углом с углом φ₁=30º в таблице 3.3. с результатами.

Таблица 3.3. Результаты расчета

№ п/п	Параметры	Формула	Размерность	Результат

	x_A		м	0,076
	y_A		м	0,044
	y_B		м	0,386
			-	-0,217
			-	0,977
			-	-0,128
			м	0,085
			-	-0,218

Продолжение таблицы 3.3.


			м	-0,033
			м	0,049
			м	0,164
			м	-0,028
			м	0,079
			м	-0,049
			м	-0,036
			м	0,438
			м	0,052

Алгоритм вычислений полученный в пункте 3.4.2.1. используем для контрольного положения механизма с углом с углом φ₁=210º в таблице 3.4. с результатами.

Таблица 3.4. Результаты расчета

№ п/п	Параметры	Формула	Размерность	Результат

	x_A		м	-0,076
	y_A		м	-0,044
	y_B		м	0,298
			-	0,217
			-	0,977
			-	0,128
			м	-0,066
			-	0,218

Продолжение таблицы 3.4.


			м	0,055
			м	-0,049
			м	0,076
			м	0,028
			м	-0,079
			м	0,049
			м	0,052
			м	0,438
			м	0,140

Сравним результаты расчетов, полученные графическим и аналитическим методами для 3-го положения, в таблице 3.5, а для 9-го в таблице 3.6.

Таблица 3.5. Сравнение полученных результатов.

Переменная	Размерность	Аналитический метод	Графический метод
y_B	м	0,386	0,382
	град.	102,5
	м	0,049	0,05
	м	0,164	0,162
	–	-0,128	0,131
	м	0,085	0,086
	м	-0,028	0,028
	м	0,079	0,080

Таблица 3.6. Сравнение полученных результатов.

Предыдущая 123 4 5 6 7 Следующая

Не нашли, что искали? Воспользуйтесь поиском по сайту: