|
|
Двумерное вращение вокруг произвольной осиВыше было рассмотрено вращение изображения около начала координат. Однородные координаты обеспечивают поворот изображения вокруг точек, отличных от начала координат. В общем случае вращение около произвольной точки может быть выполнено путем переноса центра вращения в начало координат, поворотом относительно начала координат, а затем переносом точки вращения в исходное положение. Таким образом, поворот вектора положения [х у 1 ] около точки (т, п) на произвольный угол может быть выполнен с помощью преобразования
Выполнив две операции умножения матриц, можно записать
Предположим, что центр изображения имеет координаты (4, 3) и желательно повернуть изображение на 90° против часовой стрелки вокруг центральной его оси. Действие, выполненное с помощью матрицы
вызывает вращение вокруг начала координат, а не вокруг оси. Как сказано выше, необходимо вначале осуществить перенос изображения таким образом, чтобы желаемый центр вращения находился в начале координат. Это осуществляется с помощью матрицы переноса
Затем следует применить матрицу вращения и, наконец, привести результаты к началу координат посредством обратной матрицы. Вся операция
может быть объединена в одну матричную операцию путем выполнения матричных преобразований вида
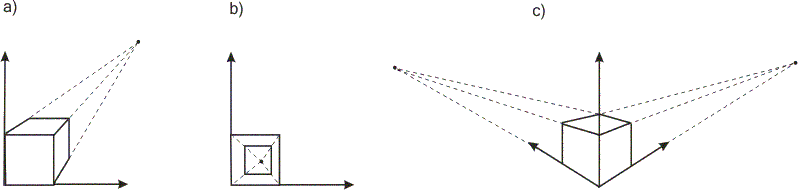
В результате будет получено х* =Х/Н и у* = Y/H. Двумерные вращения около каждой оси ортогональной системы представлены на рис. 6.5.
Рис. 6.5. Вращение: a — вокруг оси х; б — вокруг оси y; в — вокруг оси z Трехмерные преобразования Рассмотрим трехмерную декартовую систему координат, являющуюся правосторонней. Примем соглашение, в соответствии с которым будем считать положительными такие повороты, при которых (если смотреть с конца полуоси в направлении начала координат) поворот на 90° против часовой стрелки будет переводить одну полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат:
Аналогично тому, как точка на плоскости описывается вектором (x,y), точка в трехмерном пространстве описывается вектором (x,y,z). Как и в двухмерном случае, для возможности реализаций трехмерных преобразований с помощью матриц перейдем к однородным координатам:
[x,y,x,1] или [X,Y,Z,H] [x*,y*,z*1] = [ Обобщенная матрица преобразования 4´4 для трехмерных однородных координат имеет вид Т= Эта матрица может быть представлена в виде четырех отдельных частей:
· Матрица 3´3 осуществляет линейное[5] преобразование в виде изменения масштаба, сдвига и вращения. · Матрица 1´3 производит перенос. · Матрица 3´1- преобразования в перспективе. · Скалярный элемент 1´1 выполняет общее изменение масштаба. Рассмотрим воздействие матрицы 4´4 на однородный вектор [x,y,z,1]:
1. Трехмерный перенос – является простым расширением двумерного: T(Dx,Dy,Dz)=
т. е. [x,y,z,1]*T(Dx,Dy,Dz)=[x+Dx,y+Dy,z+Dz,1].
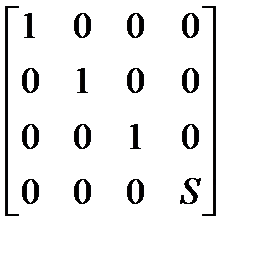
Трехмерное изменение масштаба Рассмотрим частичное изменение масштаба. Оно реализуется следующим образом: S(Sx,Sy,Sz,1)= т. е. [x,y,z,1]*S(Sx,Sy,Sz)=[Sx*x,Sy*y,Sz*z,1]. Общее изменение масштаба получается за счет 4-го диагонального элемента, т. е.
[x y z 1] *
Такой же результат можно получить при равных коэффициентах частичных изменений масштабов. В этом случае матрица преобразования такова: S=
Трехмерный сдвиг Недиагональные элементы матрицы 3´3 осуществляют сдвиг в трех измерениях, т. е. [x y z 1]* Трехмерное вращение Двухмерный поворот, рассмотренный ранее, является в то же время трехмерным поворотом вокруг оси Z . В трехмерном пространстве поворот вокруг оси Z описывается матрицей
Rz( Матрица поворота вокруг оси X имеет вид Rx( Матрица поворота вокруг оси Y имеет вид
Ry( Результатом произвольной последовательности поворотов вокруг осей x, y, z является матрица А= Подматрицу 3´3 называют ортогональной, так как ее столбцы являются взаимно ортогональными единичными векторами. Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и сдвига нет. Проекции В общем случае проекции преобразуют точки, заданные в системе координат размерностью n, в системы координат размерностью меньше чем n. Будем рассматривать случай проецирования трех измерений в два. Проекция трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проекционных лучей, которые называются проекторами и которые проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.
Рис. 6.7. Центральная и параллельная проекции Определенный таким образом класс проекций существует под названием плоских геометрических проекций, так как проецирование производится на плоскость, а не на искривленную поверхность и в качестве проекторов используются прямые, а не кривые линии. Многие картографические проекции являются либо не плоскими, либо не геометрическими. Плоские геометрические проекции в дальнейшем будем называть просто проекциями. Проекции делятся на два основных класса (рис. 6.7): § параллельные (аксонометрические); § центральные (перспективные). Полная классификация проекций приведена на рис. 6.8.
Параллельные проекции делятся на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости (рис. 6.9): 1) ортографические – направления совпадают, т. е. направление проецирования является нормалью к проекционной плоскости; 2) косоугольные – направление проецирования и нормаль к проекционной плоскости не совпадают.
Рис. 6.9. Ортографические и косоугольные проекции Наиболее широко используемыми видами ортографических проекций является вид спереди, вид сверху(план) и вид сбоку, в которых картинная плоскость перпендикулярна главным координатным осям. Если проекционные плоскости не перпендикулярны главным координатным осям, то такие проекции называются аксонометрическими. При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояние можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами). Изометрическая проекция – нормаль к проекционной плоскости, (а следовательно и направление проецирования) составляет равные углы с каждой из главных координатных осей. Если нормаль к проекционной плоскости имеет координаты (a,b,c), то потребуем, чтобы |a| = |b| = |c|, или ±a=±b=±c, т. е. имеется 8 направлений (по одному в каждом из октантов), которые удовлетворяют этому условию. Однако существует лишь 4 различных изометрических проекции (если не рассматривать удаление скрытых линий), так как векторы (a, a, a) и (-a,-a,-a) определяют нормали к одной и той же проекционной плоскости. Изометрическая проекция (рис. 6.10) обладает следующим свойством: все три главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом. Кроме того, главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом (120°).
Рис. 6.10. Изометрическая проекция единичного куба Косоугольные (наклонные) проекции сочетают в себе свойства ортографических проекций (видов спереди, сверху и сбоку) со свойствами аксонометрии. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерить углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Отметим, что нормаль к проекционной плоскости и направление проецирования не совпадают. Двумя важными видами косоугольных проекций являются проекции: · Кавалье (cavalier) – горизонтальная косоугольная изометрия (военная перспектива); · Кабине (cabinet) – фронтальная косоугольная диметрия.
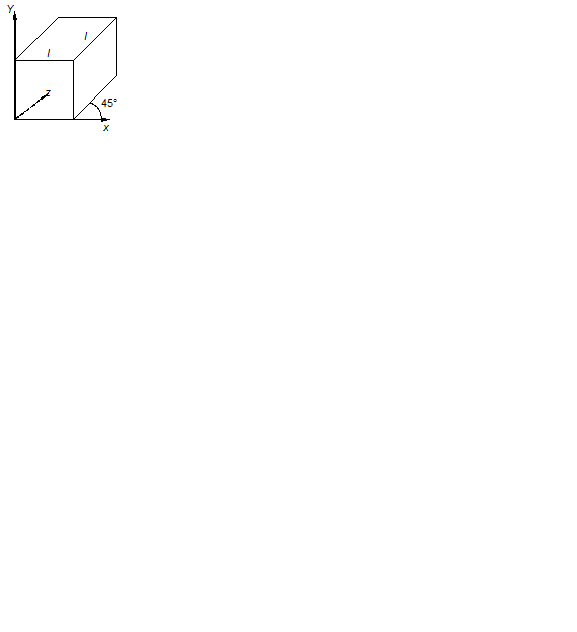
Рис. 6.11. Проекция Кавалье В проекцииКавалье (рис. 6.11) направление проецирования составляет с плоскостью угол 45°. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т. е. укорачивание отсутствует.
Рис. 6.12. Проекция Кабине ПроекцияКабине (рис. 6.12) имеет направление проецирования, которое составляет с проекционной плоскостью угол Центральнаяпроекция любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будет сходиться в точке схода. Точек схода бесконечно много. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Имеются только три такие точки, соответствующие пересечениям главных координатных осей с проекционной плоскостью. Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, а следовательно и от числа координатных осей, которые пересекают проекционную плоскость. 1. Одноточечнаяпроекция (рис. 6.13).
Рис. 6.13. Одноточечная перспектива 2. Двухточечнаяпроекция (рис. 6.14) широко применяется в архитектурном, инженерном и промышленном проектировании.
Рис. 6.14. Двухточечная перспектива 3. Трехточечныецентральные проекции почти совсем не используются, во-первых, потому, что их трудно конструировать, а во-вторых, из-за того, что они добавляют мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.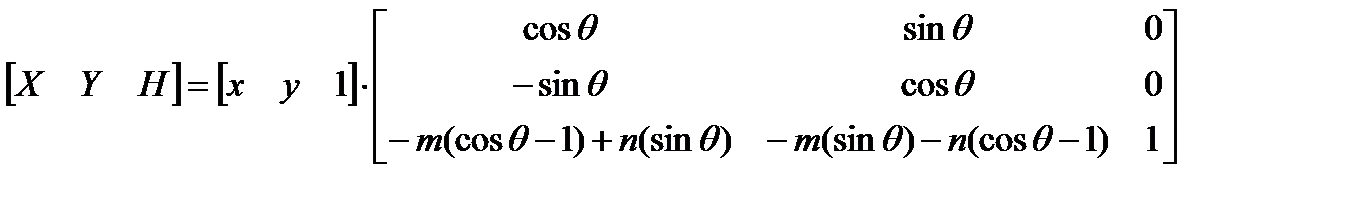
 ,
, .
.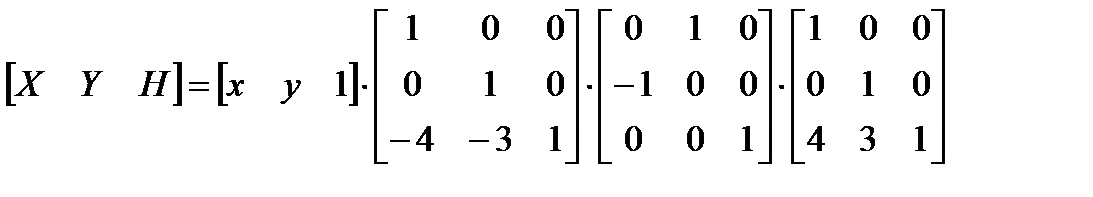
 .
. Рис. 6.6. Трехмерная система координат
Рис. 6.6. Трехмерная система координат ], где Н¹1, Н ¹0.
], где Н¹1, Н ¹0.
 .
. ,
, ,
, = [x y z S] = [x* y* z* 1] = [
= [x y z S] = [x* y* z* 1] = [ 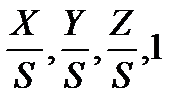 ].
]. .
. =[x+yd+hz, bx+y+iz, cx+fy+z, 1].
=[x+yd+hz, bx+y+iz, cx+fy+z, 1]. )=
)=  .
. )=
)=  .
. .
. .
.
 Рис. 6.8. Классификация проекций
Рис. 6.8. Классификация проекций

 = arctg(½) (≈26,5°). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют ½ их действительной длины. Проекции Кабине являются более реалистическими, чем проекции Кавалье, так как укорачивание с коэффициентом ½ больше согласуется с нашим визуальным опытом.
= arctg(½) (≈26,5°). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют ½ их действительной длины. Проекции Кабине являются более реалистическими, чем проекции Кавалье, так как укорачивание с коэффициентом ½ больше согласуется с нашим визуальным опытом.