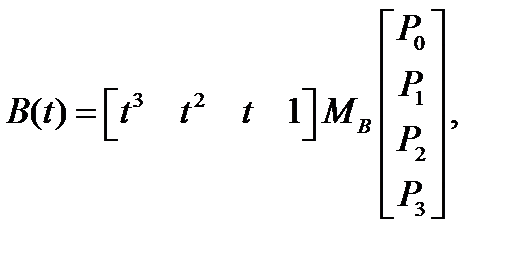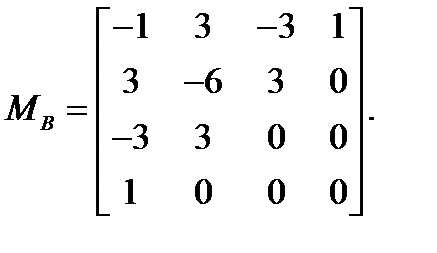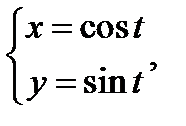|
|
Растровая развёртка окружностиСуществует несколько очень простых, но не эффективных способов преобразования окружностей в растровую форму. Например, рассмотрим для простоты окружность с центром в начале координат. Ее уравнение записывается как x2 + y2 = R2. Решая это уравнение относительно y, получим y = ±
Чтобы изобразить четвертую часть окружности, будем изменять x с единичным шагом от 0 до R и на каждом шаге вычислять y. Вторым простым методом растровой развертки окружности является использование вычислений x и y по формулам x = R cos α, y = R sin α при пошаговом изменении угла α от 0° до 90°. Для упрощения алгоритма растровой развёртки стандартной окружности можно воспользоваться её симметрией относительно координатных осей и прямых y = ± x; в случае, когда центр окружности не совпадает с началом координат, эти прямые необходимо сдвинуть параллельно так, чтобы они прошли через центр окружности. Тем самым достаточно построить растровое представление для 1/8 части окружности, а все оставшиеся точки получить симметрией (см. рис. 4.5).
Рис. 4.5. Восьмисторонняя симметрия Рассмотрим участок окружности из второго октанта x Є [0, R/ На каждом шаге алгоритм выбирает точку Pi (xi, yi), которая является ближайшей к истинной окружности. Идея алгоритма заключается в выборе ближайшей точки при помощи управляющих переменных, значения которых можно вычислить в пошаговом режиме с использованием небольшого числа сложений, вычитаний и сдвигов. Рассмотрим небольшой участок сетки пикселей, а также возможные способы (от A до E) прохождения истинной окружности через сетку (рис. 4.6). Предположим, что точка Pi-1была выбрана как ближайшая к окружности при x = xi-1. Теперь найдем, какая из точек (Si или Ti) расположена ближе к окружности при x = xi-1 + 1.
Рис. 4.6. Варианты прохождения окружности через растровую сетку Заметим, что ошибка при выборе точки Pi (xi, yi) была равна D(Pi) = (xi2+ yi2) – R2.
Запишем выражение для ошибок, получаемых при выборе точки Si или Ti:
D(Si) = [(xi-1+ 1)2 + (yi-1)2] – R2; D(Ti) = [(xi-1+ 1)2 + (yi-1 – 1)2] – R2.
Если | D(Si) | ≥ | D(Ti) |, то Ti ближе к реальной окружности, иначе выбирается Si. Введем di = | D(Si) | – | D(Ti) |.
Ti будет выбираться при di ≥ 0, в противном случае будет устанавливаться Si. Опуская алгебраические преобразования, запишем di и di+1 для разных вариантов выбора точки Si или Ti.
D1 = 3 – 2 R.
Если выбирается Si (когда di < 0), то di+1 = di + 4 xi-1 + 6. Если выбирается Ti (когда di ≥ 0), то di+1 = di + 4 (xi-1 – yi-1) + 10. Существует модификация алгоритма Брезенхейма для эллипса. Кривые Безье Кривые Безье были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Касталье (Кастельжо) из компании «Ситроен», где применялись для проектирования кузовов автомобилей. Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для представления гладких линий. Построение кривых Безье является решением задачи аппроксимации, то есть построения кривой по узловым точкам. При этом кривая не обязательно проходит через данные точки. В случае кривых Безье, кривая проходит через первую и последнюю точку, а промежуточные точки играют роль рычагов, задающих форму кривой. Кривая Безье это параметрическая кривая, задаваемая выражением: где Pi – функция компонент векторов опорных вершин, а bi,n(t) – базисные функции кривой Безье, называемые также полиномами Бернштейна.
где n – степень полинома, i – порядковый номер опорной вершины. Наглядный метод построения этих кривых, предложенный де Кастелье, основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков:
Нижний индекс – номер опорной точки, верхний индекс – уровень разбиения. Уравнение n-ого порядка задается Вид кривой зависит от количества опорных точек. Наиболее часто используются линейные, квадратные, кубические и кривые четвертого порядка. Линейные кривые При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением: B(t) = (1–t) P0 + t P1 t Є [0, 1].
Квадратные кривые Квадратная кривая Безье (n = 2) задаётся 3-я опорными точками: P0, P1 и P2. Кривая задаётся уравнением: B(t) = (1–t)2 P0 +2t(1-t) P1 + t2P2 t Є [0, 1].
Данное уравнение можно получить с помощью метода де Касталье следующим образом. Обозначим опорные точки, как
таким образом, получим кривую второго порядка. Точки
Рис. 4.7. Кривая Безье с тремя опорными точками Кубические кривые В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
B(t) = (1–t)3 P0 + 3t(1-t)2 P1 + 3t2(1-t) P2 + t3 P3 t Є [0, 1].
Для получения этой формулы используем аналогичным способом метод де Касталье. Обозначим опорные точки, как
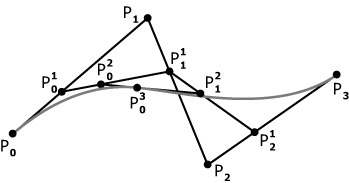
таким образом, получим кривую третьего порядка (рис. 4.8).
Рис. 4.8. Кривая Безье с четырьмя опорными точками Четыре опорные точки P0, P1, P2 и P3, заданные в двух или трехмерном пространстве определяют форму кривой. Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3. В матричной форме кубическая кривая Безье записывается следующим образом:
где MB называется базисной матрицей Безье:
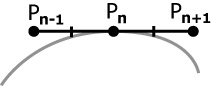
Сплайн Безье Кривые Безье обладают рядом свойств: 1. непрерывность заполнения сегмента между начальной и конечной точками; 2. инвариантность относительно аффинных преобразований. Как следствие поворот вокруг точки, масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности; 3. кривая Безье принадлежит выпуклой оболочке опорных точек, т.е. кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки; 4. если все опорные точки лежат на одной прямой, то кривая Безье вырождается в отрезок, соединяющий эти точки; 5. кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой; 6. степень многочлена, представляющего кривую в аналитическом виде, на единицу меньше числа опорных точек. Одним из главных свойств кубических кривых Безье является возможность составления из них сплайнов. Понятие сплайна пришло из машиностроения, где сплайном называли гибкую линейку, закрепив которую в нужных местах, добивались плавной формы кривой, и затем чертили ее по этой линейке. В математике под сплайном обычно понимают кусочно-заданную функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения. В случае с кривыми Безье сплайн обычно составляется из нескольких кубических кривых. Если точка Pn является стыковочной точкой, для соблюдения условия гладкости кривой в ней, необходимо, что бы выполнялось условие коллинеарности с соседними узловыми точками (рис. 4.9).
Рис. 4.9. Соблюдение условия гладкости на стыке кривых Безье Однако даже такие достаточно развитые средства аппроксимации кривыми Безье не позволяют построить окружность, описываемую параметрически как:
так как sin и cos для достаточно хорошего приближения требуют многочленов высокой степени. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. ]. Далее опишем алгоритм Брезенхейма для этого участка окружности.
]. Далее опишем алгоритм Брезенхейма для этого участка окружности.

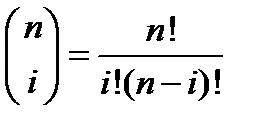
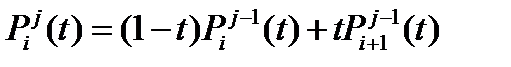
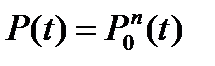
 , начало кривой положим в точке P0 (t = 0) , а конец - в точке P2 (t = 1); для каждого t Є [0, 1] найдем точку
, начало кривой положим в точке P0 (t = 0) , а конец - в точке P2 (t = 1); для каждого t Є [0, 1] найдем точку  :
: ,
, ,
, ,
,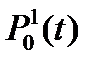 и
и  лежат на кривых первого порядка (отрезках) соединяющие опорные точки P0 с P1 и P1 c P2 соответственно. Точки, образующие кривую Безье,
лежат на кривых первого порядка (отрезках) соединяющие опорные точки P0 с P1 и P1 c P2 соответственно. Точки, образующие кривую Безье,  лежат на отрезке, соединяющем
лежат на отрезке, соединяющем 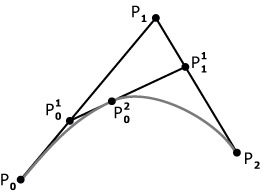
 , начало кривой положим в точке P0 (t = 0) , а конец - в точке P3 (t = 1); для каждого t Є [0, 1] найдем точку
, начало кривой положим в точке P0 (t = 0) , а конец - в точке P3 (t = 1); для каждого t Є [0, 1] найдем точку  :
: ,
, ,
,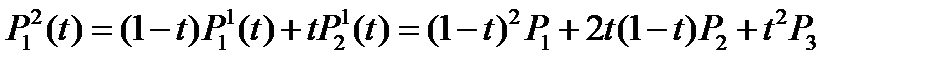 ,
, ,
,