Заполнение многоугольников

Рассмотрим, каким образом можно заполнить многоугольник, задаваемый замкнутой ломаной линией без самопересечений.

Простейший способ закраски многоугольника состоит в проверке принадлежности каждой точки этому многоугольнику. Более эффективные алгоритмы используют тот факт, что соседние пиксели, вероятно, имеют одинаковые характеристики (кроме пикселей граничных ребер). Это свойство называется пространственной когерентностью.

В случае с многоугольником когерентность пикселей определяется вдоль сканирующей строки. Сканирующие строки обычно изменяются от «верха» многоугольника до его «низа». Характеристики пикселей изменяются только там, где ребро многоугольника пересекает строку. Эти пересечения делят сканирующую строку на области закрашенных и не закрашенных пикселей.

Рассмотрим, какие случаи могут возникнуть при делении многоугольника на области сканирующей строкой.

Рис. 4.12. Прохождение сканирующих строк по многоугольнику

1. Простой случай. Например, на рис. 4.12 сканирующая строка y = 4 пересекает многоугольник при x = 1 и x = 6. Получается три области: x < 1; 1 ≤ x ≤ 6; x > 8. Сканирующая строка y = 6 пересекает многоугольник при x = 1; x = 2; x = 5; x = 6. Получается пять областей: x < 1; 1 ≤ x ≤ 2; 2 < x < 5; 5 ≤ x ≤ 6; x > 6. В этом случае x сортируется в порядке возрастания. Далее список иксов рассматривается попарно. Между парами точек пересечения закрашиваются все пиксели. Для y = 4 закрашиваются пиксели в интервале (1, 6), для y = 6 закрашиваются пиксели в интервалах (1, 2) и (5, 6).

2. Сканирующая строка проходит через вершину (рис. 4.13). Например, по сканирующей строке y = 3 упорядоченный список x получится как (2, 2, 4). Вершина многоугольника была учтена дважды, и поэтому закрашиваемый интервал получается неверным: (2, 2). Следовательно, при пересечении вершины сканирующей строкой она должна учитываться единожды. И список по х в приведенном примере будет (2, 4).

3. Сканирующая строка проходит через локальный минимум или максимум (см. рис. 4.12 при y = 5). В этом случае учитываются все пересечения вершин сканирующей строкой. На рис. 4.12 при y = 5 формируется список x (1, 4, 4, 6). Закрашиваемые интервалы (1, 4) и (4, 6). Условие нахождения локального минимума или максимума определяется при рассмотрении концевых вершин для ребер, соединенных в вершине. Если у обоих концов координаты y больше, чем y вершины пересечения, то вершина – локальный минимум. Если меньше, то вершина пересечения – локальный максимум.

Рис. 4.13. Прохождение сканирующий строки через вершину

Для ускорения работы алгоритма используется список активных ребер (САР). Этот список содержит те ребра многоугольника, которые пересекают сканирующую строку. При пересечении очередной сканирующей строки вершины многоугольника, из САР удаляются ребра, которые находятся выше, и добавляются концы, которые пересекает сканирующая строка. При работе алгоритма находятся пересечения сканирующей строки только с ребрами из САР.

Методы устранения ступенчатости

Основная причина появления лестничного эффекта заключается в том, что отрезки, ребра многоугольника, цветовые границы и пр. имеют непрерывную природу, тогда как растровые устройства дискретны.

Лестничный эффект проявляется:

1) при визуализации мелких деталей;

2) при прорисовке ребер и границ;

3) при анимации мелких деталей.

Опишем основные методы устранения ступенчатости.

Метод увеличения частоты выборки

Первый метод устранения ступенчатости связан с увеличением частоты выборки. Увеличение частоты выборки достигается с помощью увеличения разрешения растра. Таким образом учитываются более мелкие детали. Каждый пиксель делится на подпиксели в процессе формирования растра более высокого разрешения. Для получения атрибутов дисплейного пикселя определяются атрибуты в центре каждого подпикселя, которые потом усредняются. Подпиксели в этом случае распределяются равномерно и их атрибуты учитываются одинаково.

В некоторой степени можно получить лучшие результаты, если рассматривать больше подпикселей и учитывать их влияние с помощью весов при определении атрибутов.

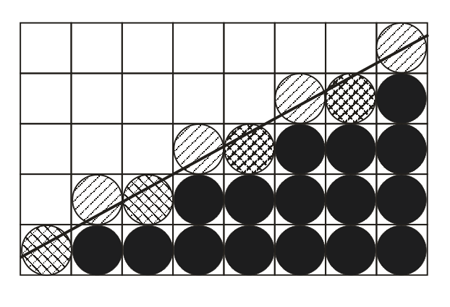
Числа обозначают относительные веса каждого подпикселя.

Метод, основанный на использовании полутонов

В этом эвристическом методе интенсивность пикселя на ребре устанавливается пропорционально площади части пикселя, находящегося внутри многоугольника.

Рис. 4.14. Закраска ребра

На рис. 4.14 приводится многоугольник, ребро которого сгенерировано основным алгоритмом Брезенхейма. Пиксели в этом ребре и внутренние пиксели многоугольника полностью закрашены. Пиксели, находящиеся выше ребра, закрашиваются с различной интенсивностью, которая пропорциональна площади пикселя, попадающего внутрь многоугольника.

Методы обработки изображений

Часто в компьютерной графике возникает задача обработки изображений. Обработка, как правило, заключается в наложении на изображение каких-либо эффектов – это размытие, резкость, деформация, шум и т. д., а также в регулировке уровня яркости и контраста.

Яркость и контраст

Яркость и контраст являются субъективными характеристиками изображения, воспринимаемыми человеком.

Яркость (brightness) представляет собой характеристику, определяющую то, на сколько сильно цвета пикселей отличаются от чёрного цвета. Например, если оцифрованная фотография сделана в солнечную погоду, то ее яркость будет значительной. С другой стороны, если фотография сделана вечером или ночью, то её яркость будет невелика.

В цветовом пространстве RGB , яркость можно рассматривать как среднее арифметическое μ красного, зеленого и синего цвета координаты. В цветовых моделях как HSB или HSV значение яркости указано на прямую.

Контраст (contrast) представляет собой характеристику того, насколько большой разброс имеют цвета пикселей изображения. Чем больший разброс имеют значения цветов пикселей, тем больший контраст имеет изображение.

По аналогии с терминами теории вероятностей можно отметить, что яркость представляет собой как бы математическое ожидание значений выборки, а контраст – дисперсию значений выборки.

Яркость и контраст могут рассматриваться не только для всего изображения, но и для отдельных фрагментов. Таким образом, возникают понятия локальной яркости и локального контраста.

Часто требуется изменить яркость или контраст изображения. Рассмотрим функцию, областью определения и значений которой являются значения цветовых компонент в модели RGB. Аргументом функции является цвет пикселя исходного изображения. Значение функции представляет собой цвет пикселя обработанного изображения. Для изменения яркости/контраста функция применяется для каждого пикселя изображения.

Для нормализации выходных значений функции (они должны принадлежать отрезку [0, 1], как для каждого компонента модели RGB) используется так называемая арифметика с насыщением. В арифметике с насыщением при возникновении переполнений или заёмов фиксируется наибольшее представимое или наименьшее представимое значения соответственно. Например, если в результате преобразования оказывается, что значение какого-либо компонента модели RGB меньше 0, то берётся значение, равное 0. На практике же каждый элемент матрицы изображения с 16777216 цветами представляет собой 24-битное значение, где каждый компонент модели RGB представлен 8-ю битами. Поэтому вместо интервала [0, 1] используется интервал [0, 255].

Если яркость и контраст изображения никак не меняются в процессе преобразования, то функция имеет график, представленный на рис. 4.15, а. Из рисунка видно, что функция в этом случае просто передаёт на выход значение своего аргумента.

a б в

Рис. 4.15. Графики яркости

Яркость для рассматриваемой функции представляет собой сдвиг прямой линии в вертикальном направлении. Яркость изображения увеличивается пропорционально сдвигу прямой. Если прямая сдвигается вверх (рис. 4.15, б), яркость изображения увеличивается, а если прямая сдвигается вниз (рис. 4.15, в) – уменьшается.

Поскольку используется арифметика с насыщением, то при установке определённой яркости изображения либо оно полностью окажется засвеченным, либо полностью затемнённым.

При использовании преобразования контраста прямая линия меняет свой наклон. При увеличении контраста изображения (рис. 4.16, а) наклон прямой увеличивается, при уменьшении контраста – уменьшается (рис. 4.16, б). При этом сдвиг прямой в горизонтальном направлении означает, что помимо контраста изменяется и яркость изображения.

а б

Рис. 4.16. Графики контрастности

Комбинации наклона и сдвига прямой позволяют одновременно изменять и яркость, и контраст изображения. Например, на рис. 4.17 представлен график функции, усиливающей контраст и увеличивающей яркость изображения.

Рис. 4.17. Увеличение яркости и контрастности

Преобразование яркости/контраста может быть применено и к отдельным компонентам модели RGB, например к компоненту красного цвета. Тогда яркость/контраст будут изменяться только для красного компонента, а для других компонент они останутся неизменными. Более того, можно задавать различные преобразования яркости/контраста одновременно для каждого компонента модели RGB.

Не нашли, что искали? Воспользуйтесь поиском по сайту: