
|
|
Определение нелицевых гранейПусть F — некоторая грань многогранника. Плоскость, несущая эту грань, разделяет пространство на два подпространства. Назовем положительным то из них, в которое смотрит внешняя нормаль к грани. Если точка наблюдения – в положительном подпространстве, то грань – лицевая, в противном случае – нелицевая. Если многогранник выпуклый, то удаление всех нелицевых граней полностью решает задачу визуализации с удалением невидимых граней. Для определения, лежит ли точка в положительном подпространстве, используют проверку знака скалярного произведения (l, n), где l – вектор, направленный к наблюдателю, фактически определяет точку наблюдения; n – вектор внешней нормали грани. Если (l, n) > 0, т. е. угол между векторами острый, то грань является лицевой. Если (l, n) < 0, т. е. угол между векторами тупой, то грань является нелицевой. В алгоритме Робертса требуется, чтобы все изображаемые тела или объекты были выпуклыми. Невыпуклые тела должны быть разбиты на выпуклые части. В этом алгоритме выпуклое многогранное тело с плоскими гранями должно представиться набором пересекающихся плоскостей. Уравнение произвольной плоскости в трехмерном пространстве имеет вид
В матричной форме этот результат выглядит так:
[x y z 1][P]T = 0,
где [P]T = [a b c d] представляет собой плоскость. Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т. е.
[V] =
где каждый столбец содержит коэффициенты одной плоскости. Напомним, что любая точка пространства представима в однородных координатах вектором [S] = [х у z 1]. Более того, если точка [S] лежит на плоскости, то [S]·[P]T = 0. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предполагается, что точки, лежащие внутри тела, дают отрицательное скалярное произведение, т. е. нормали направлены наружу. Чтобы проиллюстрировать эти идеи, рассмотрим следующий пример. Рассмотрим единичный куб с центром в начале координат (рис. 8.8).
Рис. 8.8. Куб с центром в начале координат Шесть плоскостей, описывающих данный куб, таковы: x1 = 1/2, x2 = -1/2, y3 = 1/2, y4 = -1/2, z5 = 1/2, z6 = -1/2. Более подробно уравнение правой плоскости можно записать как x1 + 0×y1+ 0×z1- (1/2) = 0 или 2x1 - 1 = 0 Полная матрица тела такова:
[V]=
Экспериментально проверим матрицу тела с помощью точки, о которой точно известно, что она лежит внутри тела. Если знак скалярного произведения для какой-нибудь плоскости больше нуля, то соответствующее уравнение плоскости следует умножить на -1. Для проверки возьмем точку внутри куба с координатами x = 1/4, y = 1/4, z = 1/4. В однородных координатах эта точка представляется в виде вектора
[S] = [1/4 1/4 1/4 1] = [1 1 1 4]. Скалярное произведение этого вектора на матрицу объема равно [S]×[V] = [1 1 1 4] ×
= [-2 6 -2 6 -2 6].
Здесь результаты для второго, четвертого и шестого уравнения плоскостей (столбцов) положительны и, следовательно, составлены некорректно. Умножая эти уравнения (столбцы) на -1, получаем корректную матрицу тела для куба: [V] =
В приведенном примере корректность уравнений плоскостей была проверена экспериментально. Разумеется, это не всегда возможно. Существует несколько полезных методов для более общего случая. Хотя уравнение плоскости содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы d = 1. Следовательно, трех неколлинеарных точек достаточно для определения этих коэффициентов. Подстановка координат трех неколлинеарных точек (x1, y1, z1), (x2, y2, z2), (х3, у3, z3) в нормированное уравнение (8.1.) дает
ax1+ by1+ cz1 = -1;
ax2+ by2 + cz3 = -1;
ax3+ by2+ cz3 = -1.
В матричной форме это выглядит так:
или
Решение этого уравнения дает значения коэффициентов уравнения плоскости: [C] = [X]-1[D]. Другой способ используется, если известен вектор нормали к плоскости, т. е.
n = ai + bj + ck,
где i, j, k – единичные векторы осей х, у, z соответственно. Тогда уравнение плоскости примет вид
Величина d вычисляется с помощью произвольной точки на плоскости. В частности, если компоненты этой точки на плоскости (х1, у1, z1), то
Перед началом работы алгоритма удаления невидимых линий или поверхностей для получения желаемого вида сцены часто применяется трехмерное видовое преобразование. Матрицы тел для объектов преобразованной сцены можно получить или преобразованием исходных матриц тел, или вычислением новых матриц тел, используя преобразованные вершины или точки. Если [В] – матрица однородных координат, представляющая исходные вершины тела, а [T] – матрица размером 4´4 видового преобразования, то преобразованные вершины таковы:
где [BT] – преобразованная матрица вершин. Использование уравнения (8.2.) позволяет получить уравнения исходных плоскостей, ограничивающих тело:
где [V] – матрица тела, а [D] в правой части – нулевая матрица. Аналогично уравнения преобразованных плоскостей задаются следующим образом:
где [VT] – преобразованная матрица тела. Приравнивая левые части уравнения (8.6.) и (8.7.), получаем
[BT][VT] = [B][V].
Подставляя уравнение (8.5.), сокращая на [В] и умножая слева на [T]-1, имеем
[VT] = [T]-1[V].
Итак, преобразованная матрица тела получается умножением исходной матрицы тела слева на обратную матрицу видового преобразования. Тот факт, что плоскости имеют бесконечную протяженность и что скалярное произведение точки (вектора точки) на матрицу тела положительно, если точка лежит вне этого тела, позволяет предложить метод, в котором матрица тела используется для определения граней, которые экранируются самим этим телом. Положительное скалярное произведение дает только такая плоскость (столбец) в матрице тела, относительно которой точка лежит снаружи, т. е. в положительном подпространстве. Проиллюстрируем это на примере уже рассмотренного единичного куба (рис. 8.9):
Условие [Е]·[V] < 0 определяет, что плоскости — нелицевые, а их грани — задние. Заметим, что для аксонометрических проекций (точка наблюдения в бесконечности) это эквивалентно поиску положительных значений в третьей строке матрицы тела. Найдем произведение [Е]·[V] для нашего примера (рис. 8.9):
[E]×[V] = [0 0 1 0] ×
Отрицательное число в шестом столбце показывает, что грань с этим номером нелицевая. Положительное число в пятом столбце показывает, что грань лицевая. Нулевые результаты соответствуют плоскостям, параллельным направлению взгляда. Положительный результат вектора E и вектора нормали можно интерпретировать как острый угол между этими векторами, отрицательный результат – как тупой угол. Если угол между векторами острый, то грань является лицевой; если угол тупой, то грань – нелицевая. Этот метод является простейшим алгоритмом удаления невидимых поверхностей для тел, представляющих собой одиночные выпуклые многогранники. Он также используется для удаления нелицевых или задних граней из сцены перед применением одного из алгоритмов удаления невидимых линий, которые обсуждаются ниже. Этот способ часто называют отбрасыванием задних плоскостей. Для выпуклых многогранников число граней при этом сокращается примерно наполовину. Метод эквивалентен вычислению нормали к поверхности для каждого отдельного многоугольника. Данный метод определения нелицевых граней в результате формирует аксонометрическую проекцию на некую плоскость, расположенную бесконечно далеко от любой точки трехмерного пространства. Видовые преобразования, включая перспективное, производятся до определения нелицевых плоскостей. Когда видовое преобразование включает в себя перспективу, то нужно использовать полное перспективное преобразование одного трехмерного пространства в другое, а не перспективное проецирование на некоторую двумерную плоскость. Полное перспективное преобразование приводит к искажению трехмерного тела, которое затем проецируется на некую плоскость в бесконечности, когда нелицевые плоскости уже определены. Этот результат эквивалентен перспективному проецированию из некоторого центра на конечную плоскость проекции. В литературе описаны и другие способы удаления невидимых граней. Так, в источнике [7] все нормали к граням тела направляются внутрь тела и используется вектор, направленный от наблюдателя к проекционной плоскости. Удаление невидимых ребер После первого этапа удаления нелицевых отрезков необходимо выяснить, существуют ли такие отрезки, которые экранируются другими телами в картинке или в сцене. Для этого каждый оставшийся отрезок или ребро нужно сравнить с другими телами сцены или картинки. Возможны следующие случаи: ¨ Грань ребра не закрывает. Ребро остается в списке ребер. ¨ Грань полностью закрывает ребро. Ребро удаляется из списка рассматриваемых ребер. ¨ Грань частично закрывает ребро. В этом случае ребро разбивается на несколько частей, видимыми из которых являются не более двух. Само ребро удаляется из списка рассматриваемых ребер, но в список проверяемых ребер добавляются те его части, которые данной гранью не закрываются. Для оптимизации используется приоритетная сортировка (z-сортировка), а также, сравнения с прямоугольными объемлющими оболочками тел. Такой подход позволяет удалить целые группы или кластеры отрезков и тел. Например, если все тела в сцене упорядочены в некотором приоритетном списке, использующем значения z ближайших вершин для представления расстояния до наблюдателя, то никакое тело из этого списка, у которого ближайшая вершина находится дальше от наблюдателя, чем самая удаленная из концевых точек ребра, не может закрывать это ребро. Более того, ни одно из оставшихся тел, прямоугольная оболочка которого расположена полностью справа, слева, над или под ребром, не может экранировать это ребро. Использование этих приемов значительно сокращает число тел, с которыми нужно сравнивать каждый отрезок или ребро. Рис. 8.10 иллюстрирует работу алгоритма.
Рис. 8.10. Результат работы алгоритма Робертса 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,
 =
= 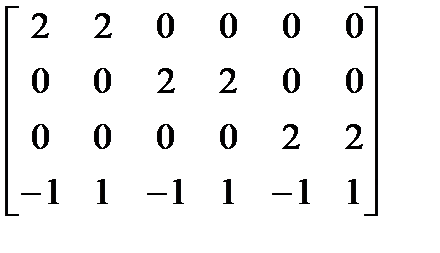 .
. =
= .
.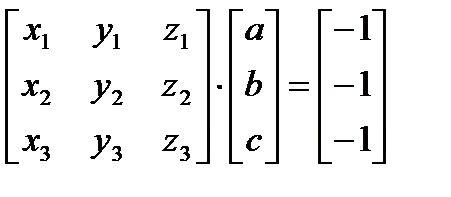
 = [0 0 0 0 2 -2].
= [0 0 0 0 2 -2].