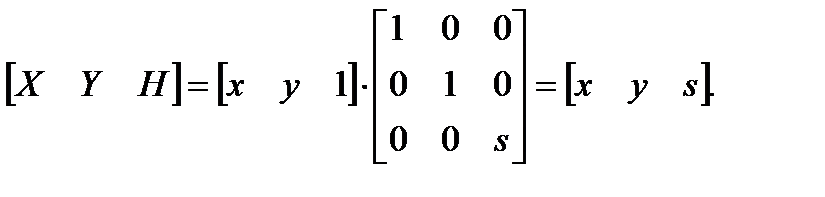|
|
Преобразование единичного квадратаЧетыре вектора положения точек единичного квадрата с одним углом в начале координат записываются в виде
Применение общего матричного преобразования
Рис. 6.1. Преобразования единичного квадрата Из полученного соотношения можно сделать вывод, что координаты В* определяются первой строкой матрицы преобразования, а координаты D* второй строкой этой матрицы. Таким образом, если координаты точек В* и D* известны, то общая матрица преобразования определена. Воспользуемся этим свойством для нахождения матрицы преобразования для вращения на произвольный угол. Общую матрицу 2´2, которая осуществляет вращение фигуры относительно начала координат, можно получить из рассмотрения вращения единичного квадрата вокруг начала координат.
Рис. 6.2. Вращение единичного квадрата Как следует из рис. 6.2, точка В с координатами (1,0) преобразуется в точку В*, для которой х*=(1)cos q и y=(1)sin q, а точка D, имеющая координаты (0,1) переходит в точку D* с координатами x*=(-1)sin q и y*=(1)cos q. Матрица преобразования общего вида записывается так:
Для частных случаев. Поворот на 90° можно осуществить с помощью матрицы преобразования
Если использовать матрицу координат вершин, то получим, например:
Поворот на 180° получается с помощью матрицы Отображение В то время как чистое двумерное вращение в плоскости xy осуществляется вокруг оси, перпендикулярной к этой плоскости, отображение определяется поворотом на 180° вокруг оси, лежащей в плоскости ху. Такое вращение вокруг линии у = х происходит при использовании матрицы Преобразованные новые выражения определяются соотношением
Вращение вокруг у = 0 получается при использовании матрицы
Однородные координаты Преобразования переноса, масштабирования и поворота записываются в матричной форме в виде
Очевидно, что перенос, в отличие от масштабирования и поворота, реализуется с помощью сложения. Это обусловлено тем, что вводить константы переноса внутрь структуры общей матрицы размером 2´2 не представляется возможным. Желательным является представление преобразований в единой форме – с помощью умножения матриц. Эту проблему можно решить за счет введения третьей компоненты в векторы точек
Это необходимо, поскольку число столбцов в матрице, описывающей точку, должно равняться числу строк в матрице преобразования для выполнения операции умножения матриц. Таким образом,
откуда следует, что константы т, п вызывают смещение х* и y* относительно х и у. Поскольку матрица 3´2 не является квадратной, она не имеет обратной матрицы. Эту трудность можно обойти, дополнив матрицу преобразования до квадратной размером 3´3. Например,
Заметим, что третья компонента векторов положения точек не изменяется при добавлении третьего столбца к матрице преобразования. Используя эту матрицу в соотношении, получаем преобразованный вектор [х* у* 1]. Добавление третьего элемента к вектору положения и третьего столбца к матрице преобразования позволяет выполнить смещение вектора положения. Третий элемент здесь можно рассматривать как дополнительную координату вектора положения. Итак, вектор положения [х у 1] при воздействии на него матрицы 3´3 становится вектором положения в общем случае вида [X Y Н]. Представленное преобразование было выполнено так, что [X Y Н] = [х* у* 1]. Преобразование, имеющее место в трехмерном пространстве, в нашем случае ограничено плоскостью, поскольку H = 1. Если, однако, третий столбец Плоскость, в которой теперь лежит преобразованный вектор положения, находится в трехмерном пространстве. Однако сейчас нас не интересует то, что происходит в трехмерном пространстве. Итак, найденные х* и у* получены с помощью пучка лучей, проходящих через начало координат. Результат преобразований показан на рис. 6.3.
Рис. 6.3. Геометрическое представление однородных координат Из рассмотрения подобных треугольников видно, что
Представление двумерного вектора трехмерным или в общем случае n-мерного вектора (п + 1)-мерным называют однородным координатным воспроизведением. При однородном координатном воспроизведении n-мерного вектора оно выполняется в (п + 1)-мерном пространстве, и конечные результаты в n-мерном пространстве получают с помощью обратного преобразования. Таким образом, двумерный вектор [х у] представляется трехкомпонентным вектором
Не существует единственного однородного координатного представления точки в двумерном пространстве. Например, однородные координаты (12, 8, 4), (6, 4, 2) и (3, 2, 1) представляют исходную точку [3 2]. Для простоты вычислений выбираем [х у 1], чтобы представить непреобразованную точку в двумерных однородных координатах. Преобразование
в дополнительных координатах задается выражением в однородных координатах в виде
Выполнение указанных выше преобразований показывает, что Х = х*, Y = у*, а Н = 1. Равенство единице дополнительной координаты означает, что преобразованные однородные координаты равны исходным координатам. В общем случае Н ¹ 1, и преобразованные обычные координаты получаются за счет нормализации однородных координат, т. е.
Геометрически все преобразования х и у происходят в плоскости Н = 1 после нормализации преобразованных однородных координат. Преимущество введения однородных координат проявляется при использовании матрицы преобразований общего вида порядка 3´3
с помощью которой можно выполнять и другие преобразования, такие как смещение, операции изменения масштаба и сдвига, обусловленные матричными элементами а, b, с и d. Указанные операции рассмотрены ранее. Чтобы показать воздействие третьего столбца матрицы преобразований 3´3, рассмотрим следующую операцию:
здесь Х = х, Y = у, а Н = рх + qy + 1. Переменная Н, которая определяет плоскость, содержащую преобразованные точки, представленные в однородных координатах, теперь образует уравнение плоскости в трехмерном пространстве. Это преобразование показано на рис. 6.4, где линияАВ, лежащая в плоскости ху, спроектирована на линиюCD плоскости рХ + qY —Н + 1 = 0. Рис. 6.4. Преобразование отрезка в однородных координатах На рисунке величина р = q = 1.Выполним нормализацию для того, чтобы получить обычные координаты:
Полагая р = q = 1, для изображенных на рисунке точек А и В с координатами соответственно (1, 3) и (4, 1) получим
После преобразования А в С* иВ в D* имеем
Однородные координаты для точек С* и D*, показанные на рисунке, соответственно равны Результатом нормализации является перевод трехмерной линии CD в ее проекцию C*D* на плоскость Н = 1. Как показано на рисунке, центром проекции является начало координат. Основная матрица преобразования размером 3´3 для двумерных однородных координат может быть подразделена на четыре части:
Как мы видим, а, b, с и d осуществляют изменение масштаба, сдвиг и вращение; т и п выполняют смещение, а р и q — получение проекций. Оставшаяся часть матрицы, элемент s, производит полное изменение масштаба. Чтобы показать это, рассмотрим преобразование
Здесь Х = х, Y = у, а Н = s. Это дает х* = x/s и y* == y/s. В результате преобразования [х у 1 ] —> [x/s y/s 1] имеет место однородное изменение масштаба вектора положения. При s< 1 происходит увеличение, а при s >1 — уменьшение масштаба. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
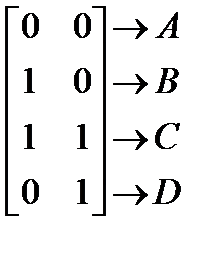
 к единичному квадрату приводит к следующему:
к единичному квадрату приводит к следующему: .
.

 .
. .
. .
.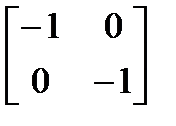 .
. .
. .
. .
. ,
,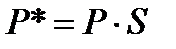 ,
, .
. и
и  , т. е. представляя их в виде
, т. е. представляя их в виде 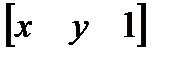 и
и 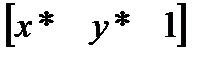 . Матрица преобразования после этого становится матрицей размером 3´2:
. Матрица преобразования после этого становится матрицей размером 3´2: .
. ,
, .
. матрицы преобразования Т размера 3 х 3 отличен от 0, то в результате матричного преобразования получим [х у 1] =[Х Y Н], где Н ¹ 1.
матрицы преобразования Т размера 3 х 3 отличен от 0, то в результате матричного преобразования получим [х у 1] =[Х Y Н], где Н ¹ 1. и
и  . Рассматривая три компоненты, запишем это в виде
. Рассматривая три компоненты, запишем это в виде .
. . Разделив компоненты вектора на однородную координату h, получим
. Разделив компоненты вектора на однородную координату h, получим и
и 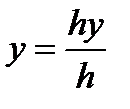 .
.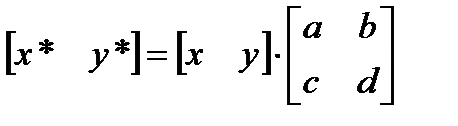
 .
.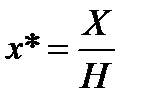 и
и  .
. ,
, ;
; ,
,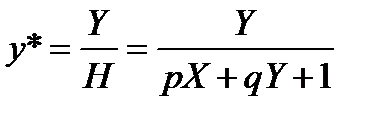
 и
и  .
.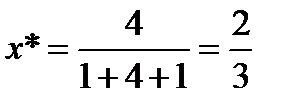 и
и  .
. и
и  .
. .
.