Полярное уравнение гиперболы
Пусть в канонической системе координат уравнение гиперболы  . Введем систему координат так: началом системы координат является точка . Введем систему координат так: началом системы координат является точка  , а полярной осью является ось , а полярной осью является ось 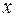 , где , где 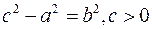 . Тогда для правой ветви гиперболы имеем: если точка . Тогда для правой ветви гиперболы имеем: если точка  принадлежит правой ветви гиперболы, то расстояние от принадлежит правой ветви гиперболы, то расстояние от  до директрисы до директрисы  равно расстоянию от фокуса до директрисы плюс равно расстоянию от фокуса до директрисы плюс  . Обозначим расстояние от фокуса до директрисы через . Обозначим расстояние от фокуса до директрисы через  . Тогда . Тогда 

Если  принадлежит левой ветви гиперболы, то расстояние от точки принадлежит левой ветви гиперболы, то расстояние от точки  до директрисы равно до директрисы равно  . .
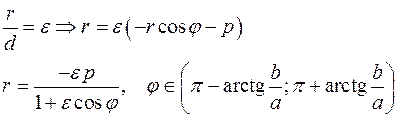
Парабола
Определение 69
Параболой называется множество точек плоскости, для которых расстояния до фиксированной точки  и до фиксированной прямой и до фиксированной прямой  равны. Точка равны. Точка  называется фокусом параболы, а прямая называется фокусом параболы, а прямая  - директрисой параболы. - директрисой параболы.
Замечание
Если точка  принадлежит прямой принадлежит прямой  , то множество таких точек – прямая, перпендикулярная , то множество таких точек – прямая, перпендикулярная  и проходящая через и проходящая через  . Поэтому будем считать, что . Поэтому будем считать, что  . .
Выберем систему координат:

Расстояние  от от  до до  равно равно  . Расстояние от . Расстояние от  до фокуса до фокуса  равно равно  . Так как . Так как  , то , то

Проверим, что каждая точка  удовлетворяющая уравнению удовлетворяющая уравнению  принадлежит этой параболе. Расстояние от точки принадлежит этой параболе. Расстояние от точки  до до  равно равно  . .
Расстояние от точки  до прямой до прямой  равно равно  . Эти расстояния равны, значит точка . Эти расстояния равны, значит точка  принадлежит параболе. принадлежит параболе.
Определение 70
Уравнение вида  ( (  ) называется каноническим уравнением параболы. ) называется каноническим уравнением параболы.
Определение 71
Система координат, в которой парабола имеет каноническое уравнение, называется канонической системой координат.
Свойства параболы
1) Парабола имеет одну ось симметрии. Точка пересечения этой оси с параболой называется вершиной параболы.
2) Парабола не имеет центра симметрии.
Определение 72
Для параболы эксцентриситет полагают равным 1.
Полярное уравнение параболы.
Поместим начало координат в фокус параболы  . Тогда расстояние до фокуса равно . Тогда расстояние до фокуса равно  , а расстояние до директрисы равно , а расстояние до директрисы равно  . Эти два расстояния равны, т.е. . Эти два расстояния равны, т.е.

Теорема 24
Пусть на плоскости заданы прямая  и точка и точка  . Тогда множество точек, для которых отношение расстояний до точки . Тогда множество точек, для которых отношение расстояний до точки  и до прямой и до прямой  равно равно 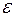 является является
1) эллипсом при  ; ;
2) гиперболой, при 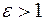 ; ;
3) параболой, при  . .
Исследование уравнений второго порядка
Определение 73
Линией второго порядка называется линия, задаваемая в некоторой декартовой системе координат уравнением:
 , где , где  . .
Пусть в некоторой декартовой системе координат линия задана уравнением  . Найдем систему координат, в которой линия задается более простым уравнением. Для этого будем рассматривать переходы от одной системы координат к другой следующего вида: . Найдем систему координат, в которой линия задается более простым уравнением. Для этого будем рассматривать переходы от одной системы координат к другой следующего вида:
Поворот на угол 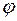 : :
 , ,  - координаты в новом базисе. - координаты в новом базисе.
Перенос начала системы координат:

Посмотрим как меняется уравнение при повороте:


Выберем угол поворота так, чтобы  . .

Если  , то , то 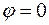 , Если , Если 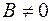 , то , то  , т.е. , т.е.  . .
Далее можно найти  и и  ( (  ). ).
При выбранном 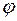 уравнение имеет вид уравнение имеет вид

Перейдем к следующей системе координат посредством сдвига:

Случай
 (т.е. (т.е.  и и  ) )


Если  ( (  ), то ), то
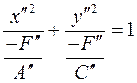
Так как  и и 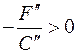 , то обозначим , то обозначим  , а , а  . .
Получим уравнение вида  . Это уравнение эллипса. . Это уравнение эллипса.
Если мы хотим получить каноническое уравнение эллипса, то требуется, чтобы коэффициент при  был меньше, чем при был меньше, чем при  . .
При  можно сделать поворот системы координат на можно сделать поворот системы координат на  и получить каноническое уравнение эллипса. и получить каноническое уравнение эллипса.
Если  , то , то
 , где , где 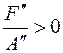 и и  . .
Точек плоскости, удовлетворяющих этому уравнению, не существует. Говорят, что данное уравнение описывает мнимый эллипс.
Если  и и  , то , то

Этому уравнению удовлетворяет одна точка с координатами 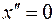 и и  . Говорят, что данное уравнение описывает вырожденный эллипс. . Говорят, что данное уравнение описывает вырожденный эллипс.
Если  и и  , то , то
 , где , где
либо  и и 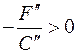 , либо , либо  и и  . .
Если  и и  , то, обозначив , то, обозначив  и и  , получим уравнение , получим уравнение  . Это каноническое уравнение гиперболы. . Это каноническое уравнение гиперболы.
Если  и и 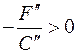 , то обозначим , то обозначим  и и  . Получим уравнение . Получим уравнение  . Перейдем к новой системе координат посредством поворота на угол . Перейдем к новой системе координат посредством поворота на угол  . .

Получим уравнение  . Это тоже каноническое уравнение гиперболы. . Это тоже каноническое уравнение гиперболы.
Если  и и  , то уравнение имеет вид , то уравнение имеет вид
 . Обозначим . Обозначим 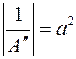 , ,  . Тогда . Тогда

Уравнение описывает пару пересекающихся прямых
 и и  . Точка пересечения прямых . Точка пересечения прямых  . .
Случай

Пусть  . Тогда . Тогда  (уравнение второго порядка). Тогда уравнение имеет вид (уравнение второго порядка). Тогда уравнение имеет вид
 С С
Если  , то , то

Преобразуем уравнение к виду 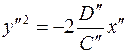 . .
Если  , то , то  является каноническим уравнением параболы. является каноническим уравнением параболы.
Если  , то для получения из уравнения , то для получения из уравнения  канонического уравнения параболы надо перейти к системе координат посредством поворота на угол канонического уравнения параболы надо перейти к системе координат посредством поворота на угол  . .
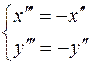
В этой системе координат уравнение имеет вид 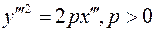 . .
Если  , то , то

Преобразуем это уравнение к виду
 . Если . Если 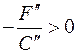 , то, обозначив , то, обозначив  , получаем уравнение , получаем уравнение  . Это уравнение двух параллельных прямых . Это уравнение двух параллельных прямых  и и  . .
Если  , то, обозначив , то, обозначив  , получаем уравнение , получаем уравнение  . Точек на плоскости, удовлетворяющих данному уравнению, нет. Говорят, что это уравнение описывает пару мнимых параллельных прямых. . Точек на плоскости, удовлетворяющих данному уравнению, нет. Говорят, что это уравнение описывает пару мнимых параллельных прямых.
Если  , то уравнение принимает вид , то уравнение принимает вид  . Говорят, что это уравнение описывает пару совпадающих прямых. Таким образом мы доказали теорему. . Говорят, что это уравнение описывает пару совпадающих прямых. Таким образом мы доказали теорему.
Теорема 25
Любое уравнение второго порядка путем преобразования системы координат поворотом и переносом начала системы координат можно привести к одному из видов:
1)  - эллипс. - эллипс.
2)  - вырожденный эллипс. - вырожденный эллипс.
3)  - мнимый эллипс. - мнимый эллипс.
4)  - гипербола. - гипербола.
5)  - пара пересекающихся прямых. - пара пересекающихся прямых.
6) 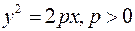 - парабола. - парабола.
7)  - пара параллельных прямых. - пара параллельных прямых.
8) 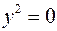 - пара совпадающих прямых. - пара совпадающих прямых.
9)  - пара мнимых параллельных прямых. - пара мнимых параллельных прямых.
Теорема 26
Для уравнения второго порядка  величины величины  , ,  , ,  являются инвариантными относительно преобразований системы координат посредством поворота и переноса начала системы координат. являются инвариантными относительно преобразований системы координат посредством поворота и переноса начала системы координат.
1) Если  , то уравнение приводится к одному из уравнений , то уравнение приводится к одному из уравнений
 или или  или или 
При  и и  получаем уравнение эллипса. получаем уравнение эллипса.
При  и и  получаем уравнение вырожденного эллипса. получаем уравнение вырожденного эллипса.
При  и и  получаем уравнение мнимого эллипса. получаем уравнение мнимого эллипса.
2) Если 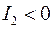 , то уравнение приводится к одному из уравнений , то уравнение приводится к одному из уравнений
 или или 
При  получаем уравнение гиперболы. получаем уравнение гиперболы.
При  получаем уравнение пары пересекающихся прямых. получаем уравнение пары пересекающихся прямых.
3) Если  , то уравнение приводится к одному из уравнений , то уравнение приводится к одному из уравнений
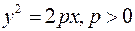 или или  или или 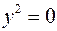 или или 
При  получаем уравнение параболы. получаем уравнение параболы.
При  получаем уравнение пары (параллельных / совпадающих / мнимых параллельных) прямых. получаем уравнение пары (параллельных / совпадающих / мнимых параллельных) прямых.
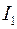
| 
| 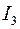
| уравнение
| 
| 
| 
|  - эллипс - эллипс
| 
|  - вырожденный эллипс - вырожденный эллипс
| 
|  - мнимый эллипс - мнимый эллипс
| 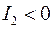
| 
|  - гипербола - гипербола
| 
|  - пара пересекающихся прямых - пара пересекающихся прямых
| 
| 
| 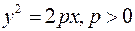 - парабола - парабола
| 
|  - пара параллельных прямых или - пара параллельных прямых или 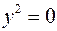 - пара совпадающих прямых или - пара совпадающих прямых или  - пара мнимых параллельных прямых - пара мнимых параллельных прямых
|
Определение 74
Кривые, для которых  называются кривыми эллиптического типа. Кривые, для которых называются кривыми эллиптического типа. Кривые, для которых 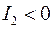 называются кривыми гиперболического типа. Кривые, для которых называются кривыми гиперболического типа. Кривые, для которых  называются кривыми параболического типа. называются кривыми параболического типа.
Определение 75
Центр симметрии кривой второго порядка называется центром кривой второго порядка.
Определение 76
Если кривая имеет ровно один центр, то такая кривая называется центральной.
Замечание
Центральными кривыми являются эллиптические и гиперболические кривые, т.е. те для которых  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . Введем систему координат так: началом системы координат является точка
. Введем систему координат так: началом системы координат является точка  , а полярной осью является ось
, а полярной осью является ось 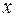 , где
, где 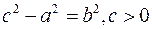 . Тогда для правой ветви гиперболы имеем: если точка
. Тогда для правой ветви гиперболы имеем: если точка  принадлежит правой ветви гиперболы, то расстояние от
принадлежит правой ветви гиперболы, то расстояние от  равно расстоянию от фокуса до директрисы плюс
равно расстоянию от фокуса до директрисы плюс  . Обозначим расстояние от фокуса до директрисы через
. Обозначим расстояние от фокуса до директрисы через  . Тогда
. Тогда 

 .
.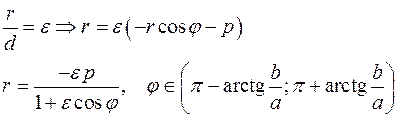
 и до фиксированной прямой
и до фиксированной прямой  равны. Точка
равны. Точка  .
.
 от
от  . Расстояние от
. Расстояние от  . Так как
. Так как  , то
, то
 удовлетворяющая уравнению
удовлетворяющая уравнению  принадлежит этой параболе. Расстояние от точки
принадлежит этой параболе. Расстояние от точки  .
. . Эти расстояния равны, значит точка
. Эти расстояния равны, значит точка  ) называется каноническим уравнением параболы.
) называется каноническим уравнением параболы. , а расстояние до директрисы равно
, а расстояние до директрисы равно  . Эти два расстояния равны, т.е.
. Эти два расстояния равны, т.е.
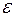 является
является ;
;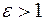 ;
; .
. , где
, где  .
.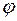 :
: ,
,  - координаты в новом базисе.
- координаты в новом базисе.


 .
.
 , то
, то 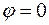 , Если
, Если 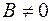 , то
, то  , т.е.
, т.е.  .
. и
и  (
(  ).
).

 (т.е.
(т.е.  и
и  )
)

 (
(  ), то
), то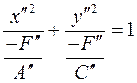
 и
и 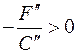 , то обозначим
, то обозначим  , а
, а  .
. . Это уравнение эллипса.
. Это уравнение эллипса. был меньше, чем при
был меньше, чем при  .
. можно сделать поворот системы координат на
можно сделать поворот системы координат на  и получить каноническое уравнение эллипса.
и получить каноническое уравнение эллипса. , то
, то , где
, где 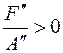 и
и  .
. и
и  , то
, то
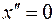 и
и  . Говорят, что данное уравнение описывает вырожденный эллипс.
. Говорят, что данное уравнение описывает вырожденный эллипс. и
и  , где
, где и
и  .
. и
и  , получим уравнение
, получим уравнение  . Это каноническое уравнение гиперболы.
. Это каноническое уравнение гиперболы. и
и  . Получим уравнение
. Получим уравнение  . Перейдем к новой системе координат посредством поворота на угол
. Перейдем к новой системе координат посредством поворота на угол 
 . Это тоже каноническое уравнение гиперболы.
. Это тоже каноническое уравнение гиперболы. . Обозначим
. Обозначим 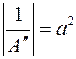 ,
,  . Тогда
. Тогда
 и
и  . Точка пересечения прямых
. Точка пересечения прямых  .
.
 . Тогда
. Тогда  С
С , то
, то
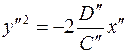 .
. , то
, то  является каноническим уравнением параболы.
является каноническим уравнением параболы. , то для получения из уравнения
, то для получения из уравнения  канонического уравнения параболы надо перейти к системе координат посредством поворота на угол
канонического уравнения параболы надо перейти к системе координат посредством поворота на угол  .
.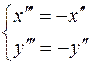
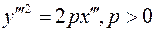 .
. , то
, то
 . Если
. Если  , получаем уравнение
, получаем уравнение  . Это уравнение двух параллельных прямых
. Это уравнение двух параллельных прямых  и
и  .
. , получаем уравнение
, получаем уравнение  . Точек на плоскости, удовлетворяющих данному уравнению, нет. Говорят, что это уравнение описывает пару мнимых параллельных прямых.
. Точек на плоскости, удовлетворяющих данному уравнению, нет. Говорят, что это уравнение описывает пару мнимых параллельных прямых. , то уравнение принимает вид
, то уравнение принимает вид  . Говорят, что это уравнение описывает пару совпадающих прямых. Таким образом мы доказали теорему.
. Говорят, что это уравнение описывает пару совпадающих прямых. Таким образом мы доказали теорему. - эллипс.
- эллипс. - вырожденный эллипс.
- вырожденный эллипс. - мнимый эллипс.
- мнимый эллипс. - пара пересекающихся прямых.
- пара пересекающихся прямых.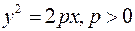 - парабола.
- парабола. - пара параллельных прямых.
- пара параллельных прямых.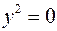 - пара совпадающих прямых.
- пара совпадающих прямых. - пара мнимых параллельных прямых.
- пара мнимых параллельных прямых. ,
,  ,
,  являются инвариантными относительно преобразований системы координат посредством поворота и переноса начала системы координат.
являются инвариантными относительно преобразований системы координат посредством поворота и переноса начала системы координат. , то уравнение приводится к одному из уравнений
, то уравнение приводится к одному из уравнений и
и  получаем уравнение эллипса.
получаем уравнение эллипса. получаем уравнение вырожденного эллипса.
получаем уравнение вырожденного эллипса. получаем уравнение мнимого эллипса.
получаем уравнение мнимого эллипса.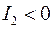 , то уравнение приводится к одному из уравнений
, то уравнение приводится к одному из уравнений получаем уравнение гиперболы.
получаем уравнение гиперболы. , то уравнение приводится к одному из уравнений
, то уравнение приводится к одному из уравнений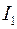

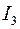
 .
.