
|
|
Преобразование аффинной системы координат на плоскостиПусть на плоскости заданы две системы координат Если у нас есть две декартовые системы координат
Пример. Поворот декартовой системы координат на угол Тогда
Координаты точки
Пример. Сдвиг системы координат (параллельный перенос).
Пример. Отражение системы координат симметрично оси вектора
Общий случай поворота со сдвигом.
Общий случай поворота, с отражением и сдвигом.
Из полученных формул можно выразить координаты точки
Кривые и поверхности на Пусть на плоскости (в пространстве) задана декартовая система координат. Определение 41 Будем говорить, что уравнение Определение 42 Будем говорить, что уравнение Определение 43 Будем говорить, что система уравнений Примеры.
Определение 44 Будем говорить, что линия на плоскости задана параметрически, если в некоторой декартовой системе координат координаты точек Определение 45 Будем говорить, что поверхность в пространстве задана параметрически, если в некоторой декартовой системе координат координаты точек поверхности заданы уравнениями Примеры. Окружность радиуса
Сфера радиуса 3 с центром в точке
Определение 46 Линия на плоскости называется алгебраической, если в некоторой декартовой системе координат она задается алгебраическим уравнением, т.е. уравнением вида Определение 47 Порядком алгебраической линии на плоскости называется порядок алгебраического уравнения задающего данную линию, т.е. Пример Линия, задаваемая уравнением Определение 48 Поверхность в пространстве называется алгебраической, если в некоторой декартовой системе координат она задается алгебраическим уравнением, т.е. уравнением вида Определение 48 Порядком алгебраической поверхности в пространстве называется порядок алгебраического уравнения задающего данную поверхность, т.е. Теорема 20 (об инвариантности порядка алгебраической линии на плоскости) Если алгебраическая линия в одной декартовой системе координат имеет порядок Доказательство. Пусть в первой системе координат линия задается уравнением
После раскрытия скобок и приведения подобных членов получим алгебраическое уравнение порядка Замечание. Алгебраическую линию в одной и той же системе координат можно задать различными алгебраическими уравнениями: Теорема 21 (об инвариантности порядка алгебраической поверхности в пространстве) Если алгебраическая поверхность имеет в декартовой системе координат порядок Прямая на плоскости и Рассмотрим на плоскости декартову систему координат. Базисные вектора буем обозначать Определение 49 Множеством точек В декартовой системе координат для точки
Теорема 22 1) Если Доказательство. 1) Пусть прямая 2) См. Вывод уравнения прямой, ортогональной заданному вектору. Определение 50 Уравнения первого порядка будем называть линейными уравнениями. Различные способы задания 1) Любая прямая на плоскости задается уравнением вида 2) Уравнение прямой, проходящий через точку 3) Уравнение в отрезках. Если прямая задается полным уравнением, т.е. 4) Нормированное уравнение. Если обозначить 5) Каноническое уравнение. Пусть дано уравнение прямой 6) Уравнение прямой, проходящей через две точки. Требуется написать уравнение прямой, проходящей через точки 7) Параметрическое задание прямой. Пусть вектор с координатами Задачи 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  . Для любого вектора
. Для любого вектора  верно равенство
верно равенство  . Так как
. Так как  - базис, то существуют числа
- базис, то существуют числа  , такие что
, такие что  . Если координаты точки
. Если координаты точки  в системе координат
в системе координат  , а в системе координат
, а в системе координат  , то они связаны соотношением
, то они связаны соотношением  . Обозначим координаты вектора
. Обозначим координаты вектора  в базисе
в базисе 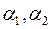 . Тогда
. Тогда 




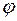 (поворот против часовой стрелки).
(поворот против часовой стрелки).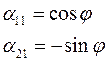


 , где
, где  в системе координат
в системе координат  .
.

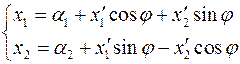

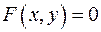 задает линию
задает линию  , если для
, если для 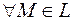 с координатами
с координатами  выполняется равенство
выполняется равенство 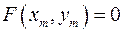 и для
и для  с координатами
с координатами 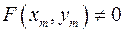 .
.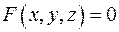 задает поверхность
задает поверхность  выполняется равенство
выполняется равенство  и для
и для  .
. задает линию
задает линию  и для
и для 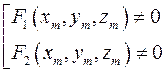 .
. (уравнение окружности на плоскости)
(уравнение окружности на плоскости) (уравнение сферы в пространстве)
(уравнение сферы в пространстве) (уравнение окружности в пространстве)
(уравнение окружности в пространстве) .
.
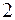 с центром в начале координат:
с центром в начале координат:
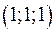 :
: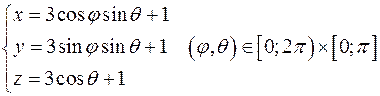

 , где
, где 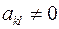 .
. имеет порядок 3. Линия, задаваемая уравнением
имеет порядок 3. Линия, задаваемая уравнением 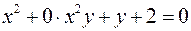 имеет порядок 2.
имеет порядок 2.
 , где
, где  .
.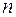 , то и в другой декартовой системе координат она может быть задана алгебраическим уравнением порядка
, то и в другой декартовой системе координат она может быть задана алгебраическим уравнением порядка  , и пусть координаты в новой системе координат связаны с исходными
, и пусть координаты в новой системе координат связаны с исходными 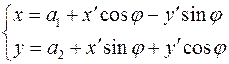 . Подставляем эти формулы в алгебраическое уравнение:
. Подставляем эти формулы в алгебраическое уравнение:
 . Подставляя в полученное уравнение выражения координат
. Подставляя в полученное уравнение выражения координат  через
через 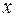 и
и 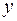 получим исходное уравнение порядка
получим исходное уравнение порядка  . Таким образом
. Таким образом  .
. .
. и
и  , начало координат
, начало координат  . Координаты точек будем обозначать
. Координаты точек будем обозначать 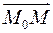 ортогонален вектору
ортогонален вектору 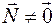 называется прямой, проходящей через точку
называется прямой, проходящей через точку 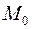 , ортогональной вектору
, ортогональной вектору  .
. 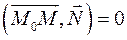 .
. , точки
, точки 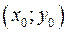 и вектора
и вектора  уравнение прямой можно записать:
уравнение прямой можно записать:
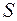 - линия на плоскости и в некоторой декартовой системе координат она задается уравнением
- линия на плоскости и в некоторой декартовой системе координат она задается уравнением 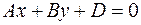 , где
, где 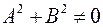 , то
, то 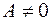 . Рассмотрим точку
. Рассмотрим точку  . Тогда для всех точек
. Тогда для всех точек  с координатами
с координатами  , удовлетворяющих уравнению
, удовлетворяющих уравнению  выполняется
выполняется  является ортогональным к этой прямой. Это уравнение называется общим уравнением прямой на плоскости.
является ортогональным к этой прямой. Это уравнение называется общим уравнением прямой на плоскости.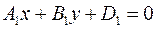 задают одну и ту же прямую, то
задают одну и ту же прямую, то 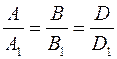 .
.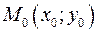 , ортогональной вектору
, ортогональной вектору  :
: .
.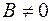 и
и  , то
, то 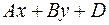 эквивалентно
эквивалентно или
или  .
.
 имеет единичную длину. Обозначим
имеет единичную длину. Обозначим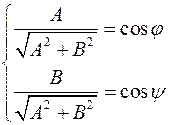 , где
, где  и
и  - направляющие косинусы.
- направляющие косинусы. , где
, где  .
. , а
, а  , где
, где  .
.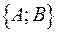 ортогонален прямой. Вектор с координатами
ортогонален прямой. Вектор с координатами 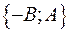 ортогонален вектору с координатами
ортогонален вектору с координатами 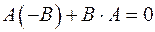 ). Таким образом вектор с координатами
). Таким образом вектор с координатами  и
и  . Получим: если вектор
. Получим: если вектор  является параллельным прямой, то уравнение прямой
является параллельным прямой, то уравнение прямой  .
. и
и  . Вектор с координатами
. Вектор с координатами  параллелен прямой. Поэтому уравнение прямой
параллелен прямой. Поэтому уравнение прямой 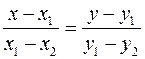 .
. коллинеарен вектору
коллинеарен вектору  . Получаем
. Получаем