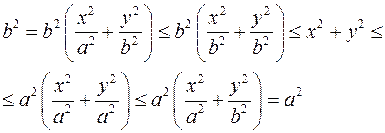Нахождение угла между прямыми
Пусть в декартовой системе координат две прямые заданы уравнениями 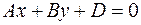 и и 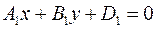 . .
Если 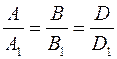 , то эти прямые совпадают. Если , то эти прямые совпадают. Если  , то эти прямые не имеют общих точек, т.е. параллельны. Пусть , то эти прямые не имеют общих точек, т.е. параллельны. Пусть 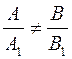 . Тогда прямые пересекаются. Так как вектор . Тогда прямые пересекаются. Так как вектор 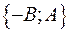 параллелен прямой параллелен прямой 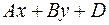 и вектор и вектор  параллелен прямой параллелен прямой 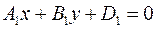 , то угол между векторам , то угол между векторам 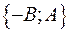 и и  совпадает с углом между векторами совпадает с углом между векторами 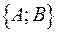 и и 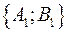 , т.е. угол между прямыми совпадает с углом между перпендикулярными прямыми. Угол между перпендикулярами может быть найден по формуле , т.е. угол между прямыми совпадает с углом между перпендикулярными прямыми. Угол между перпендикулярами может быть найден по формуле
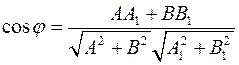
 , либо , либо 
Расстояние от точки до прямой
Пусть задано уравнение прямой 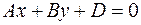 и точка и точка  . Нормируем уравнение прямой: . Нормируем уравнение прямой:
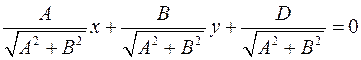 и пусть точка и пусть точка 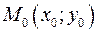 принадлежит прямой. Нормальный вектор к прямой принадлежит прямой. Нормальный вектор к прямой 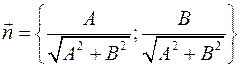 , причем , причем  . Угол между вектором . Угол между вектором 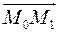 и и 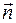 обозначим через обозначим через 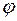 . Тогда расстояние от точки . Тогда расстояние от точки 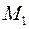 до прямой равно до прямой равно 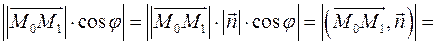

Замечание
Если точка  лежит по ту же сторону от прямой, куда направлен вектор лежит по ту же сторону от прямой, куда направлен вектор 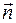 , то угол , то угол 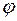 - острый и величина - острый и величина 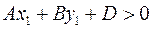 . Если точка . Если точка  лежит по другую сторону от прямой, то угол лежит по другую сторону от прямой, то угол 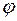 - тупой и величина - тупой и величина  . .
Задача
Построение биссектрисы угла между прямыми
Пусть даны уравнения прямых
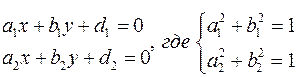
По последнему замечанию для всех точек по одну сторону от первой прямой выражение 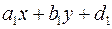 имеет положительные значения, а по другую отрицательные. Аналогично для второй прямой. Поэтому произведение величин имеет положительные значения, а по другую отрицательные. Аналогично для второй прямой. Поэтому произведение величин 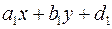 и и 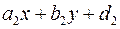 сохраняет знак в вертикальных углах. Биссектриса угла обладает тем свойством, что каждая точка на биссектрисе равноудалена от прямых. Поэтому уравнения биссектрис сохраняет знак в вертикальных углах. Биссектриса угла обладает тем свойством, что каждая точка на биссектрисе равноудалена от прямых. Поэтому уравнения биссектрис
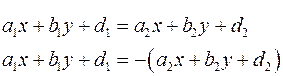
Переносим в левую сторону, и получаем
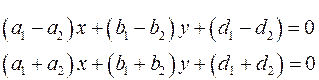
Плоскость в пространстве
Определение 51
Плоскостью  , проходящей через точку , проходящей через точку 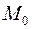 , ортогональной вектору , ортогональной вектору 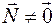 называется множество точек называется множество точек  таких, что таких, что 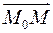 ортогонален ортогонален  , т.е. , т.е. 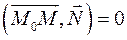 . Если вектор . Если вектор  имеет координаты имеет координаты  , точка , точка 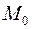 имеет координаты имеет координаты 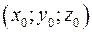 , то для точки , то для точки  с координатами с координатами 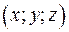 получаем уравнение принадлежности плоскости получаем уравнение принадлежности плоскости 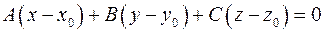 или или  , где , где 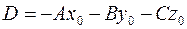 . .
Теорема 23
1) Если поверхность  в пространстве описывается уравнением в пространстве описывается уравнением  , где , где  , то , то  - плоскость, ортогональная вектору - плоскость, ортогональная вектору  . .
2) Любая плоскость может быть задана уравнением  , где , где  . .
Доказательство
1) Так как  , то будем считать, что , то будем считать, что 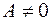 . Тогда точка . Тогда точка 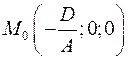 принадлежит поверхности принадлежит поверхности  и уравнение приобретает вид и уравнение приобретает вид 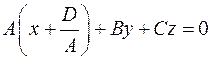 . Это выражение является скалярным произведением вектора . Это выражение является скалярным произведением вектора  и вектора с координатами и вектора с координатами 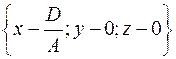 . Последний является координатами вектора . Последний является координатами вектора 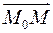 , где , где  - точка с координатами - точка с координатами 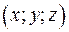 . Получили условие на принадлежность точки . Получили условие на принадлежность точки  поверхности поверхности  : : 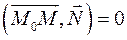 . Это условие задает плоскость (см. определение). . Это условие задает плоскость (см. определение).
2) Смотри вывод уравнения плоскости.
Способы задания плоскости в пространстве
1) Общее уравнение плоскости
Уравнение плоскости, ортогональной вектору  , проходящей через точку , проходящей через точку 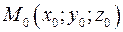 : :
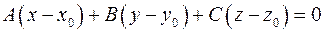 или или
 , где , где 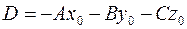
2) Пусть заданы неколлинеарные векторы  и и 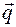 . Уравнение плоскости, проходящей через точку . Уравнение плоскости, проходящей через точку 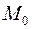 , параллельно векторам , параллельно векторам  и и 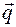 получаем следующим образом. Вектор получаем следующим образом. Вектор 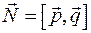 является ортогональным этой плоскости, поэтому точка является ортогональным этой плоскости, поэтому точка  принадлежит плоскости тогда и только тогда, когда принадлежит плоскости тогда и только тогда, когда 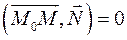
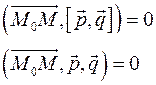
Если координаты вектора 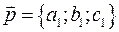 , координаты вектора , координаты вектора 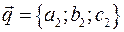 , координаты точки , координаты точки 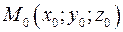 и координаты точки и координаты точки 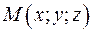 , то условие записывается , то условие записывается

3) Если даны три точки, не лежащие на одной прямой

то уравнение плоскости, проходящей через эти точки
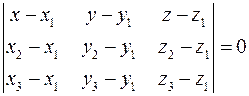
4) Параметрическое задание плоскости. Пусть заданы неколлинеарные вектора  и и 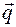 и точка и точка 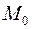 . Тогда точка . Тогда точка  принадлежит плоскости, проходящей через точку принадлежит плоскости, проходящей через точку 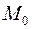 параллельно векторам параллельно векторам  и и 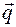 тогда и только тогда, когда вектора тогда и только тогда, когда вектора 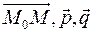 компланарны. Т.к. компланарны. Т.к.  и и 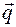 некомпланарны, то некомпланарны, то 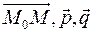 компланарны тогда и только тогда, когда найдутся такие компланарны тогда и только тогда, когда найдутся такие 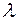 и и 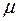 такие, что такие, что 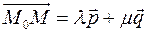 . Обозначим координаты векторов: . Обозначим координаты векторов:
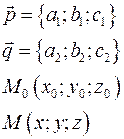
Тогда условие перепишется
 или или
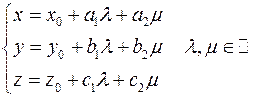
5) Нормированное уравнение плоскости
Если в общем уравнении  (или (или 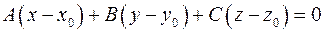 ) вектор ) вектор  обладает свойством обладает свойством 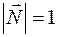 , то такое уравнение называет нормированным. , то такое уравнение называет нормированным.
Задачи
1) Угол между плоскостями
Определение 52
Углом между плоскостями называется угол, между векторами, ортогональными этим плоскостям.
Замечание
Угол между плоскостями определен неоднозначно. Межу плоскостями может быть два различных угла.
Пусть плоскости заданы уравнениями:
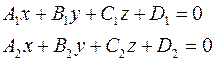
Ортогональные векторы к этим плоскостям 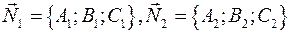
Угол 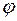 между плоскостями определяем из равенства между плоскостями определяем из равенства
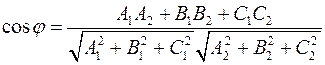
2) Расстояние от точки до плоскости
Пусть плоскость задана уравнением  и точка и точка 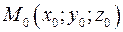 принадлежит плоскости. Запишем нормированное уравнение плоскости: принадлежит плоскости. Запишем нормированное уравнение плоскости:
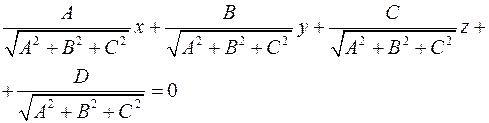
Обозначим угол между вектором с координатами  и вектором и вектором 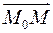 через через 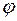 . Тогда расстояние от точки . Тогда расстояние от точки  до плоскости равно до плоскости равно 
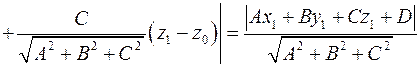 , где , где  - координаты точки - координаты точки  . .
Замечание
Если точка  лежит по ту же сторону от плоскости, куда направлен вектор лежит по ту же сторону от плоскости, куда направлен вектор  , то угол , то угол 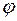 - острый и величина - острый и величина 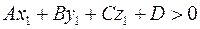 . Если точка . Если точка  лежит по другую сторону от плоскости, то угол лежит по другую сторону от плоскости, то угол 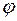 тупой и величина тупой и величина  . .
Прямая в пространстве
Две плоскости в пространстве либо параллельны, либо совпадают, либо пересекаются, и множество точек пересечения плоскостей является прямой. Поэтому прямые в пространстве удобно задавать, как пересечение плоскостей. Тогда уравнение прямой имеет вид
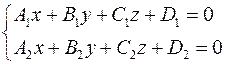 , где , где  и НЕ выполняется и НЕ выполняется 
Если прямая задана направляющим вектором  , т.е. прямая проходящая через точку , т.е. прямая проходящая через точку 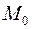 содержит точки содержит точки  такие, что такие, что 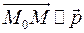 , то уравнение прямой можно записать в каноническом виде: , то уравнение прямой можно записать в каноническом виде:  , где , где 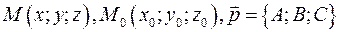
Если прямая задана пересечением плоскостей
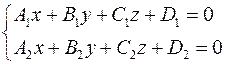 , то для написания канонического уравнения прямой надо найти направляющий вектор. , то для написания канонического уравнения прямой надо найти направляющий вектор. 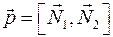 , где , где 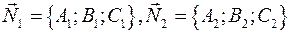 и найти точку, принадлежащую прямой. Для нахождения общей точки плоскостей можно воспользоваться методом Крамера. Пусть дана система и найти точку, принадлежащую прямой. Для нахождения общей точки плоскостей можно воспользоваться методом Крамера. Пусть дана система  и и  . Тогда . Тогда
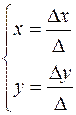 , где , где 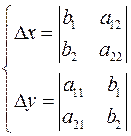
Доказательство
Домножаем первое уравнение на 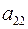 , а второе на , а второе на  и вычитаем. и вычитаем.

Аналогично 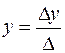
Если уравнение прямой 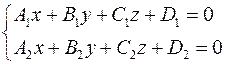 , то не выполняется пропорция , то не выполняется пропорция  . Пусть не выполняется первое, т.е. . Пусть не выполняется первое, т.е.  . Тогда взяв . Тогда взяв  подберем подберем 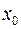 и и 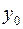 системы системы 
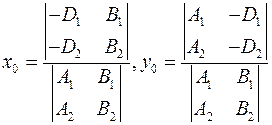
Точка с координатами 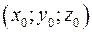 является точкой прямой. является точкой прямой.
Задачи
1) Нахождение угла между прямыми
Пусть прямые заданы уравнениями
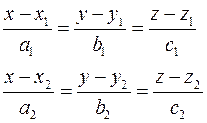
Определение 53
Углом между прямыми называется угол между направляющими векторами этих прямых. Направляющий вектор первой прямой имеет координаты 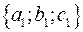 , второй прямой , второй прямой  . Угол между этими векторами . Угол между этими векторами 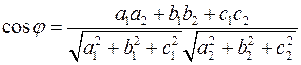
2) Условия на принадлежность прямых одной плоскости
Пусть прямые заданы уравнениями
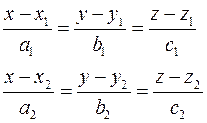
Обозначим направляющий вектор с координатами 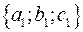 через через 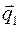 , вектор с координатами , вектор с координатами  через через 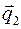 . Обозначим . Обозначим 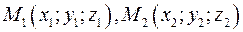 . Если прямые параллельны, то через них можно провести плоскость и векторы . Если прямые параллельны, то через них можно провести плоскость и векторы 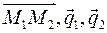 компланарны. Если прямые пересекаются, то через них можно провести плоскость и векторы компланарны. Если прямые пересекаются, то через них можно провести плоскость и векторы 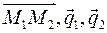 компланарны. Если прямые скрещивающиеся, то векторы компланарны. Если прямые скрещивающиеся, то векторы 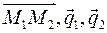 некомпланарны. Таким образом условие принадлежности прямых одной плоскости записывается некомпланарны. Таким образом условие принадлежности прямых одной плоскости записывается  или в координатах: или в координатах:
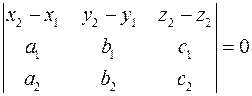
3) Угол между прямой и плоскостью
Пусть плоскость задана уравнением  , а прямая уравнением , а прямая уравнением 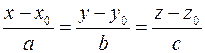 . Обозначим через . Обозначим через 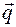 вектор с координатами вектор с координатами 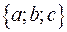 , через , через  вектор с координатами вектор с координатами  . Угол между векторами . Угол между векторами 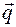 и и  через через  , угол между прямой и плоскостью, через , угол между прямой и плоскостью, через 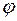 . Угол . Угол 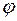 удовлетворяет неравенству удовлетворяет неравенству 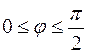 . Поэтому . Поэтому 
4) Нахождение проекции точки на плоскость
Определение 54
Проекцией точки  на плоскость на плоскость  называется точка называется точка 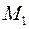 такая, что такая, что 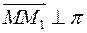 и и  . .
Пусть плоскость задана уравнением  , точка , точка  имеет координаты имеет координаты 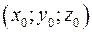 , ,  - вектор с координатами - вектор с координатами  . .
Напишем параметрическое уравнение прямой, проходящей через точку  перпендикулярно плоскости. перпендикулярно плоскости.

Точка 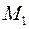 лежит на этой прямой и принадлежит плоскости, поэтому ее координаты удовлетворяют уравнению лежит на этой прямой и принадлежит плоскости, поэтому ее координаты удовлетворяют уравнению 
Координаты точки 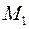
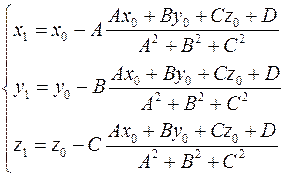
5) Проекция точки на прямую
Определение 55
Проекцией точки  на прямую на прямую  называется точка называется точка 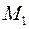 такая, что такая, что 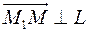 и и 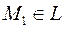 . .
Пусть прямая задана уравнением 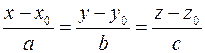 . Направляющий вектор . Направляющий вектор 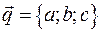 , точка , точка 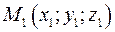 . Уравнение плоскости, проходящей через точку . Уравнение плоскости, проходящей через точку  , перпендикулярную прямой: , перпендикулярную прямой: 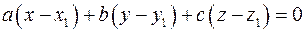 . Точка . Точка 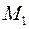 , являющаяся пересечением плоскости и прямой, является проекцией точки , являющаяся пересечением плоскости и прямой, является проекцией точки  на прямую и является проекцией точки на прямую и является проекцией точки 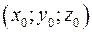 на плоскость. Параметрическое уравнение прямой: на плоскость. Параметрическое уравнение прямой:
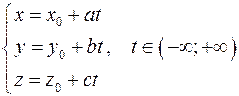
Подставляем в уравнение плоскости:
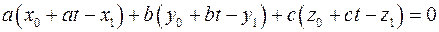
 . Таким образом координаты точки . Таким образом координаты точки  : :
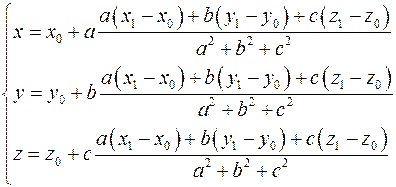
6) Уравнение прямой, перпендикулярной двум скрещивающимся прямым
Пусть заданы прямые
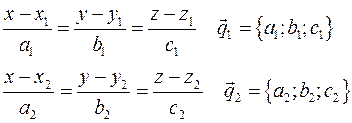
Вектор 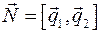 перпендикулярен первой и второй прямой, значит он является направляющим вектором прямой, перпендикулярной скрещивающимся прямым. Плоскость, проходящая через искомую прямую и первую прямую задается уравнением перпендикулярен первой и второй прямой, значит он является направляющим вектором прямой, перпендикулярной скрещивающимся прямым. Плоскость, проходящая через искомую прямую и первую прямую задается уравнением 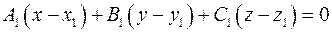 , где , где 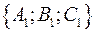 - координаты вектора - координаты вектора  . Плоскость, проходящая через искомую прямую и вторую прямую задается уравнением . Плоскость, проходящая через искомую прямую и вторую прямую задается уравнением 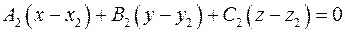 , где , где  - координаты вектора - координаты вектора  . Уравнение искомой прямой: . Уравнение искомой прямой:
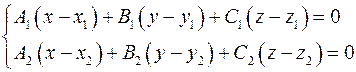
7) Расстояние между скрещивающимися прямыми в пространстве
Пусть прямые заданы уравнениями
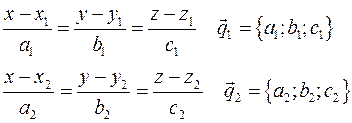
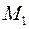 - точка с координатами - точка с координатами  , , 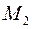 - точка с координатами - точка с координатами 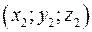 . Уравнение плоскости, проходящей через точку . Уравнение плоскости, проходящей через точку 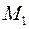 параллельно векторам параллельно векторам 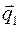 и и 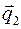 . .
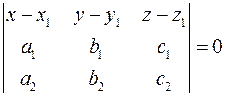
Расстояние от первой прямой до второй – это расстояние от 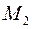 до построенной плоскости: до построенной плоскости:
8) Расстояние между параллельными плоскостями
Пусть плоскости заданы уравнениями

Пусть точка с координатами 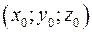 принадлежит первой плоскости, т.е. принадлежит первой плоскости, т.е. 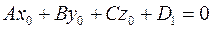 . Расстояние от первой плоскости до второй равно расстоянию от точки . Расстояние от первой плоскости до второй равно расстоянию от точки 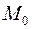 до второй плоскости. Оно равно до второй плоскости. Оно равно  . .
Кривые второго порядка
Эллипс
Определение 56
Эллипсом называется множество точек сумма расстояний от каждой из которых до точек  и и  постоянна. Точки постоянна. Точки  и и  называются фокусами эллипса. называются фокусами эллипса.
Замечание
Если точки  и и  совпадают, то полученная фигура называется окружностью. совпадают, то полученная фигура называется окружностью.
Обозначим фиксированную сумму через  , а расстояние между , а расстояние между  и и  через через  . Если . Если 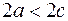 , то подходящих под определение точек на плоскости нет. Если , то подходящих под определение точек на плоскости нет. Если 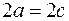 , то получается отрезок. Будем считать, что , то получается отрезок. Будем считать, что  . .
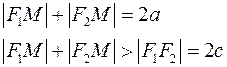 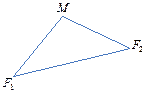
Введем декартову систему координат, в которой точка  имеет координаты имеет координаты  , а точка , а точка  координаты координаты  . .
Выведем уравнение эллипса. Пусть  принадлежит эллипсу. Тогда принадлежит эллипсу. Тогда
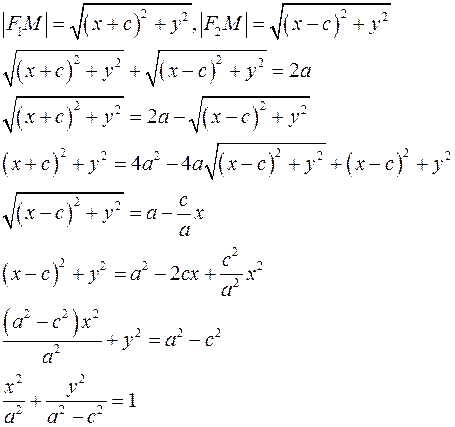
Проверим, что каждая точка удовлетворяющая этому уравнению принадлежит эллипсу. Пусть точка  удовлетворяет уравнению удовлетворяет уравнению 
Докажем, что точка  принадлежит эллипсу. принадлежит эллипсу.
Из этого уравнения имеем 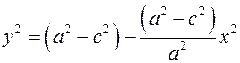 . Расстояние от точки . Расстояние от точки  до фокуса до фокуса  равно равно 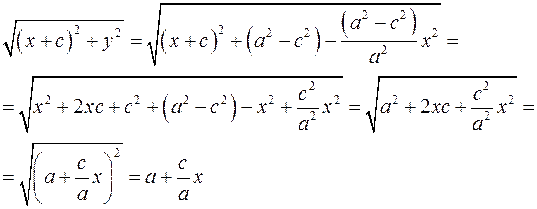
Так как 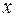 удовлетворяет уравнению удовлетворяет уравнению  , то , то  . Аналогично получаем расстояние до фокуса . Аналогично получаем расстояние до фокуса  . Оно равно . Оно равно  . Сумма полученных расстояний равна . Сумма полученных расстояний равна  , т.е. точка , т.е. точка  принадлежит эллипсу. Таким образом точка принадлежит эллипсу. Таким образом точка  принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению  . Будем обозначать . Будем обозначать 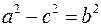 . Тогда уравнение приобретает вид . Тогда уравнение приобретает вид  , причем , причем  . .
Определение 57
Уравнение вида  , где , где  называется каноническим уравнением эллипса. называется каноническим уравнением эллипса.
Определение 58
Декартовая система координат, в которой уравнение эллипса имеет канонический вид называется канонической системой координат.
Свойства эллипса
Пусть есть каноническое уравнение эллипса  . Тогда . Тогда
1) Эллипс имеет две оси симметрии – ось ординат и ось абсцисс.
Доказательство
Пусть  - точка с координатами - точка с координатами  принадлежит эллипсу. Тогда точки принадлежит эллипсу. Тогда точки 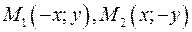 удовлетворяют уравнению эллипса удовлетворяют уравнению эллипса
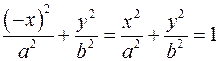 . Точка . Точка 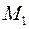 симметрична точке симметрична точке  относительно оси ординат, а точка относительно оси ординат, а точка 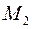 симметрична точке симметрична точке  относительно оси абсцисс. относительно оси абсцисс.
Замечание
Прямая, проходящая через фокусы является главной осью симметрии. Прямая, перпендикулярная отрезку с концами в фокусах и проходящая через его середину тоже является осью симметрии.
Определение 59
Ось симметрии, проходящая через фокусы называется большей главной осью, а перпендикулярная ей ось симметрии – малой главной осью.
Замечание
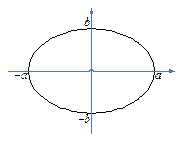 Большая главная ось пересекает эллипс в точках, которые являются концами отрезка длины Большая главная ось пересекает эллипс в точках, которые являются концами отрезка длины  . Малая главная ось пересекает эллипс в точках, которые являются концами отрезка длины . Малая главная ось пересекает эллипс в точках, которые являются концами отрезка длины 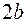 . . 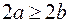 . .
Замечание
Если 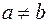 , то главные оси симметрии единственные. Если , то главные оси симметрии единственные. Если  , то главных осей бесконечно много. , то главных осей бесконечно много.
Определение 60
Точки пересечения эллипса с главными осями называются вершинами эллипса.
2) Точка пересечения главных осей является центром симметрии эллипса. В канонической системе координат точка пересечения главных осей совпадает с началом координат. Поэтому для точки эллипса  симметричной является точка симметричной является точка  . Так как . Так как  , то и , то и  , т.е. , т.е. 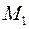 принадлежит эллипсу. принадлежит эллипсу.
Замечание
Если фигура ограничена, то на может обладать только одним центром симметрии.
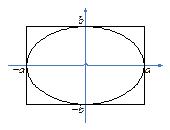 3) В канонической системе координат эллипс ограничен прямоугольником 3) В канонической системе координат эллипс ограничен прямоугольником
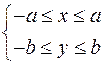
Доказательство
В канонической системе координат уравнение эллипса  , значит для точек эллипса выполняются неравенства , значит для точек эллипса выполняются неравенства 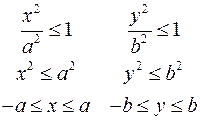
4) Рассмотрим уравнение эллипса в канонической системе координат:  . Пусть прямая . Пусть прямая  проходит через центр симметрии эллипса. Тогда длина проходит через центр симметрии эллипса. Тогда длина  отрезка, отсекаемого эллипсом на этой прямой удовлетворяет неравенству отрезка, отсекаемого эллипсом на этой прямой удовлетворяет неравенству 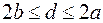 . Причем левое неравенство превращается в равенство, только если прямая является меньшей главной осью, а правое неравенство превращается в равенство, только если прямая является большей главной осью. Пусть точка . Причем левое неравенство превращается в равенство, только если прямая является меньшей главной осью, а правое неравенство превращается в равенство, только если прямая является большей главной осью. Пусть точка  принадлежит эллипсу. Тогда расстояние от точки принадлежит эллипсу. Тогда расстояние от точки  до центра симметрии удовлетворяет неравенству до центра симметрии удовлетворяет неравенству
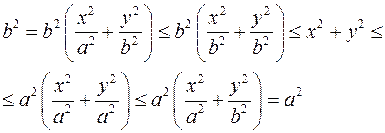

Равенство слева достигается только если точка  является вершиной и лежит на меньшей главной оси, а правое, если точка является вершиной и лежит на меньшей главной оси, а правое, если точка  является вершиной и лежит на большей главной оси. является вершиной и лежит на большей главной оси.
Определение 61
Центром эллипса будем называть центр симметрии эллипса.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


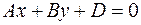 и
и 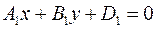 .
.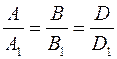 , то эти прямые совпадают. Если
, то эти прямые совпадают. Если  , то эти прямые не имеют общих точек, т.е. параллельны. Пусть
, то эти прямые не имеют общих точек, т.е. параллельны. Пусть 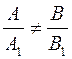 . Тогда прямые пересекаются. Так как вектор
. Тогда прямые пересекаются. Так как вектор 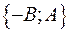 параллелен прямой
параллелен прямой 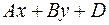 и вектор
и вектор  параллелен прямой
параллелен прямой 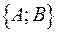 и
и 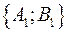 , т.е. угол между прямыми совпадает с углом между перпендикулярными прямыми. Угол между перпендикулярами может быть найден по формуле
, т.е. угол между прямыми совпадает с углом между перпендикулярными прямыми. Угол между перпендикулярами может быть найден по формуле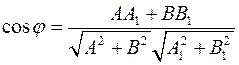
 , либо
, либо 
 . Нормируем уравнение прямой:
. Нормируем уравнение прямой: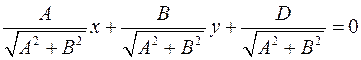 и пусть точка
и пусть точка 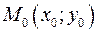 принадлежит прямой. Нормальный вектор к прямой
принадлежит прямой. Нормальный вектор к прямой 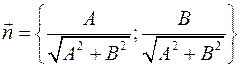 , причем
, причем  . Угол между вектором
. Угол между вектором 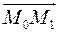 и
и 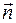 обозначим через
обозначим через 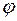 . Тогда расстояние от точки
. Тогда расстояние от точки 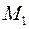 до прямой равно
до прямой равно 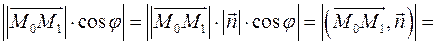

 лежит по ту же сторону от прямой, куда направлен вектор
лежит по ту же сторону от прямой, куда направлен вектор 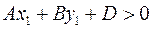 . Если точка
. Если точка  .
.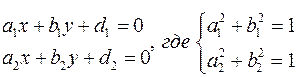
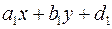 имеет положительные значения, а по другую отрицательные. Аналогично для второй прямой. Поэтому произведение величин
имеет положительные значения, а по другую отрицательные. Аналогично для второй прямой. Поэтому произведение величин 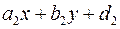 сохраняет знак в вертикальных углах. Биссектриса угла обладает тем свойством, что каждая точка на биссектрисе равноудалена от прямых. Поэтому уравнения биссектрис
сохраняет знак в вертикальных углах. Биссектриса угла обладает тем свойством, что каждая точка на биссектрисе равноудалена от прямых. Поэтому уравнения биссектрис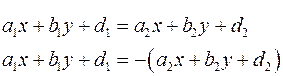
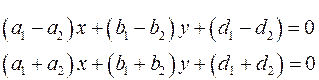
 , проходящей через точку
, проходящей через точку 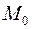 , ортогональной вектору
, ортогональной вектору 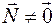 называется множество точек
называется множество точек 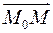 ортогонален
ортогонален  , т.е.
, т.е. 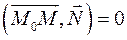 . Если вектор
. Если вектор  , точка
, точка 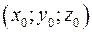 , то для точки
, то для точки 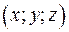 получаем уравнение принадлежности плоскости
получаем уравнение принадлежности плоскости 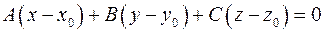 или
или  , где
, где 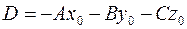 .
. , то
, то  .
.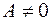 . Тогда точка
. Тогда точка 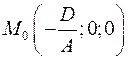 принадлежит поверхности
принадлежит поверхности 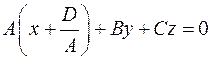 . Это выражение является скалярным произведением вектора
. Это выражение является скалярным произведением вектора 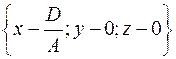 . Последний является координатами вектора
. Последний является координатами вектора 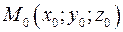 :
: и
и 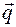 . Уравнение плоскости, проходящей через точку
. Уравнение плоскости, проходящей через точку 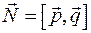 является ортогональным этой плоскости, поэтому точка
является ортогональным этой плоскости, поэтому точка 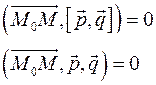
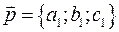 , координаты вектора
, координаты вектора 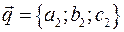 , координаты точки
, координаты точки 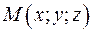 , то условие записывается
, то условие записывается

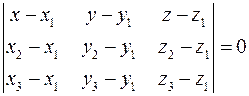
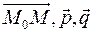 компланарны. Т.к.
компланарны. Т.к. 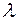 и
и 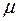 такие, что
такие, что 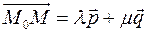 . Обозначим координаты векторов:
. Обозначим координаты векторов: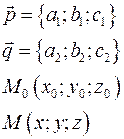
 или
или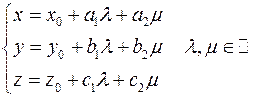
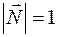 , то такое уравнение называет нормированным.
, то такое уравнение называет нормированным.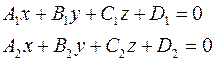
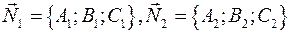
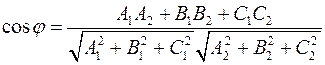
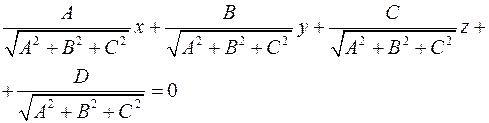
 и вектором
и вектором 
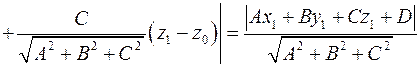 , где
, где  - координаты точки
- координаты точки 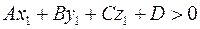 . Если точка
. Если точка  .
.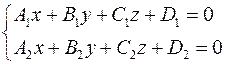 , где
, где  и НЕ выполняется
и НЕ выполняется 
 , т.е. прямая проходящая через точку
, т.е. прямая проходящая через точку 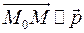 , то уравнение прямой можно записать в каноническом виде:
, то уравнение прямой можно записать в каноническом виде:  , где
, где 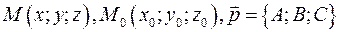
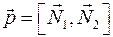 , где
, где  и
и  . Тогда
. Тогда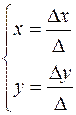 , где
, где 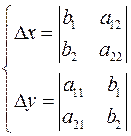
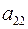 , а второе на
, а второе на  и вычитаем.
и вычитаем.
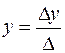
 . Тогда взяв
. Тогда взяв  подберем
подберем 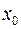 и
и 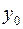 системы
системы 
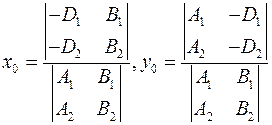
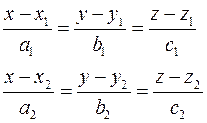
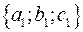 , второй прямой
, второй прямой  . Угол между этими векторами
. Угол между этими векторами 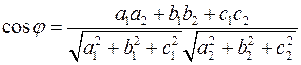
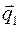 , вектор с координатами
, вектор с координатами 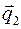 . Обозначим
. Обозначим 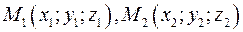 . Если прямые параллельны, то через них можно провести плоскость и векторы
. Если прямые параллельны, то через них можно провести плоскость и векторы 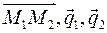 компланарны. Если прямые пересекаются, то через них можно провести плоскость и векторы
компланарны. Если прямые пересекаются, то через них можно провести плоскость и векторы  или в координатах:
или в координатах: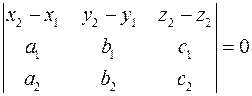
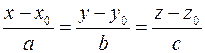 . Обозначим через
. Обозначим через 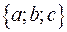 , через
, через  , угол между прямой и плоскостью, через
, угол между прямой и плоскостью, через 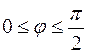 . Поэтому
. Поэтому 
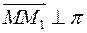 и
и  .
.

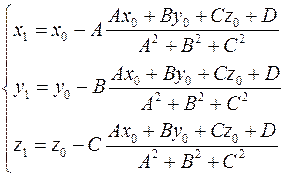
 называется точка
называется точка 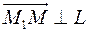 и
и 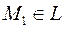 .
.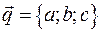 , точка
, точка 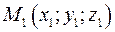 . Уравнение плоскости, проходящей через точку
. Уравнение плоскости, проходящей через точку 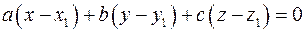 . Точка
. Точка 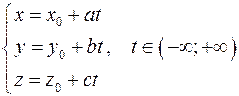
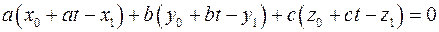
 . Таким образом координаты точки
. Таким образом координаты точки 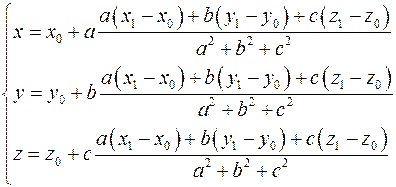
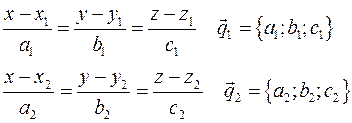
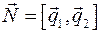 перпендикулярен первой и второй прямой, значит он является направляющим вектором прямой, перпендикулярной скрещивающимся прямым. Плоскость, проходящая через искомую прямую и первую прямую задается уравнением
перпендикулярен первой и второй прямой, значит он является направляющим вектором прямой, перпендикулярной скрещивающимся прямым. Плоскость, проходящая через искомую прямую и первую прямую задается уравнением 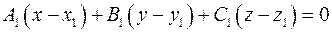 , где
, где 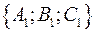 - координаты вектора
- координаты вектора  . Плоскость, проходящая через искомую прямую и вторую прямую задается уравнением
. Плоскость, проходящая через искомую прямую и вторую прямую задается уравнением 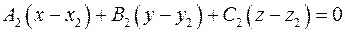 , где
, где  - координаты вектора
- координаты вектора  . Уравнение искомой прямой:
. Уравнение искомой прямой: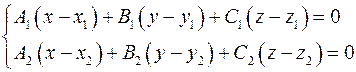
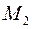 - точка с координатами
- точка с координатами 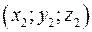 . Уравнение плоскости, проходящей через точку
. Уравнение плоскости, проходящей через точку 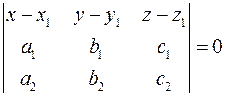
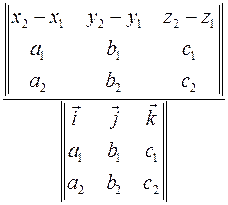

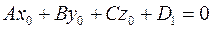 . Расстояние от первой плоскости до второй равно расстоянию от точки
. Расстояние от первой плоскости до второй равно расстоянию от точки  .
. и
и  постоянна. Точки
постоянна. Точки  , а расстояние между
, а расстояние между  . Если
. Если 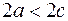 , то подходящих под определение точек на плоскости нет. Если
, то подходящих под определение точек на плоскости нет. Если 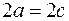 , то получается отрезок. Будем считать, что
, то получается отрезок. Будем считать, что  .
.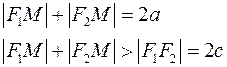

 , а точка
, а точка  .
.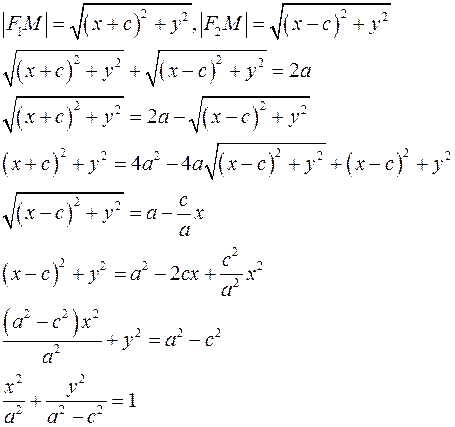

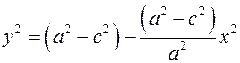 . Расстояние от точки
. Расстояние от точки 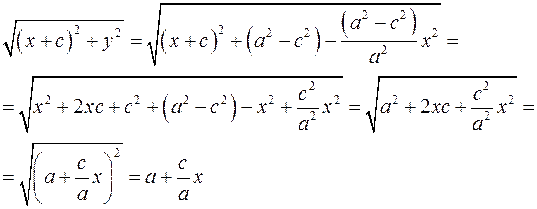
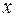 удовлетворяет уравнению
удовлетворяет уравнению  . Аналогично получаем расстояние до фокуса
. Аналогично получаем расстояние до фокуса  . Сумма полученных расстояний равна
. Сумма полученных расстояний равна  , т.е. точка
, т.е. точка 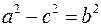 . Тогда уравнение приобретает вид
. Тогда уравнение приобретает вид  , причем
, причем  .
. принадлежит эллипсу. Тогда точки
принадлежит эллипсу. Тогда точки 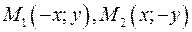 удовлетворяют уравнению эллипса
удовлетворяют уравнению эллипса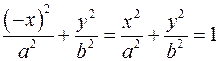 . Точка
. Точка  Большая главная ось пересекает эллипс в точках, которые являются концами отрезка длины
Большая главная ось пересекает эллипс в точках, которые являются концами отрезка длины 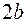 .
. 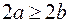 .
.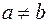 , то главные оси симметрии единственные. Если
, то главные оси симметрии единственные. Если  , то главных осей бесконечно много.
, то главных осей бесконечно много. симметричной является точка
симметричной является точка  . Так как
. Так как  , т.е.
, т.е.  3) В канонической системе координат эллипс ограничен прямоугольником
3) В канонической системе координат эллипс ограничен прямоугольником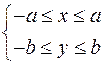
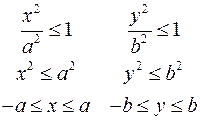
 проходит через центр симметрии эллипса. Тогда длина
проходит через центр симметрии эллипса. Тогда длина  отрезка, отсекаемого эллипсом на этой прямой удовлетворяет неравенству
отрезка, отсекаемого эллипсом на этой прямой удовлетворяет неравенству 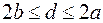 . Причем левое неравенство превращается в равенство, только если прямая является меньшей главной осью, а правое неравенство превращается в равенство, только если прямая является большей главной осью. Пусть точка
. Причем левое неравенство превращается в равенство, только если прямая является меньшей главной осью, а правое неравенство превращается в равенство, только если прямая является большей главной осью. Пусть точка