
|
|
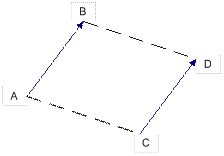
Теорема 13 (о базисе в пространстве, на плоскости, на прямой)Определение 1 Закрепленным вектором называют отрезок Можем дать определение другими словами: Закрепленным вектором называется упорядоченная пара точек. Определение 2 Закрепленный вектор, у которого начало и конец совпадает, будем называть нулевым. Определение 3 Два ненулевых закрепленных вектора, не лежащих на одной прямой будем называть равными, если при соединении отрезком их начал и соединении отрезком их концов образуется параллелограмм.
Два ненулевых вектора, лежащих на одной прямой, будем называть равными, если существует третий вектор, не лежащий с ними на одной прямой и равный обоим.
Все нулевые вектора считаем равными. Теорема 1 Отношение равенства закрепленных векторов обладает следующими свойствами: 1) рефлективность: закрепленный вектор 2) симметричность: если вектор 3) транзитивность: если вектор Доказательство 1) Если
Фигура 2) По определению. 3) а) (Векторы
Так как б) (Векторы
Так как в) (Векторы
По определению. г) (Все векторы
Пусть вектор Так как Замечание Отношения, обладающие свойством рефлективности, симметричности и транзитивности обычно называют отношениями эквивалентности. Определение 4 Классом равенства вектора Теорема 2 Классы равенства векторов либо не пересекаются, либо совпадают. Доказательство Пусть два класса равенства
Поэтому Следствие Множество всех закрепленных векторов распадается на попарно непересекающиеся классы векторов. Определение 5 Свободными векторам будем называть классы равенства закрепленных векторов. Свободные вектора будем обозначать Определение 6 Будем говорить, что свободные векторы равны, если их классы совпадают. При этом писать будем Линейные операции над векторами Под линейными операциями над векторами будем понимать сложение векторов и умножение векторов на действительные числа. Определение 7 Суммой закрепленных векторов
Определение 8 Произведением вектора Векторы
Определение 9 Суммой свободных векторов Определение 10 Произведением свободного вектора Теорема 3 Определение суммы свободных векторов и произведения свободного вектора на число корректна, то есть сумма не зависит от выбора закрепленных векторов, и произведение не зависит от выбора закрепленного вектора. Доказательство Докажем частично корректность суммы. Нам надо показать, что выбор пары
Пусть Определение 11 Свободные векторы Теорема 4 Если векторы Доказательство Рассмотрим Определение 12 Будем говорить, что на множестве Определение 13 Будем говорить, что на множестве Определение 14 Множество 1) для любых 2) для любых 3) существует элемент 4) Для каждого элемента 5) Для любого числа 6) Для любых чисел 7) Для любых чисел 8) Для любого элемента Теорема 5 Совокупность свободных векторов с введенными ранее операциями сложения и умножения на число является линейно-векторным пространством. Доказательство 1) Так как операция сложения не зависит от представителей классов равенства, то достаточно проверить на закрепленных векторах.
По свойствам параллелограмма 2) Так как операция сложения не зависит от представителей классов равенства, то достаточно проверить на закрепленных векторах.
Проверяем на представителях классов равенства. Из определения суммы получаем 3) Нулевой элемент существует по построению. Нулевым вектором является класс закрепленных векторов, у которых начало и конец совпадают. 4) Для каждого закрепленного вектора существует вектор ему коллинеарный с противоположным направлением такой, что
Для построения такого вектора достаточно отложить точку 5)
Очевидно из подобия. 6) Векторы 7) Аналогично 6). 8) Аналогично 6). Определение 15 Линейной комбинацией векторов Определение 16 Если все коэффициенты в линейной комбинации равны Определение 17 Система векторов Определение 18 Система векторов называется линейно независимой, если она не является линейно зависимой. Замечание Если Пример 1 Вектор Доказательство Возьмем Пример 2 Совокупность векторов, один их которых нулевой образует линейно зависимую систему. Доказательство Обозначим векторы Теорема 6 Если система векторов Доказательство Без ограничения общности будем считать, что подсистема векторов Следствие Если подсистема векторов Теорема 7 Два коллинеарных вектора на плоскости или в пространстве линейно зависимы. Доказательство Если хотя бы один из векторов равен Линейная комбинация равна Теорема 8 Два вектора на плоскости или в пространстве линейно независимы тогда и только тогда, когда они не коллинеарны. Доказательство Если они линейно независимые, то они не могут быть коллинеарны по теореме 6. Если два вектора Определение 19 Ненулевые векторы называются компланарными, если они лежат в одной или параллельных плоскостях. Теорема 9 Три вектора в пространстве линейно независимы тогда и только тогда, когда они не компланарны. Доказательство Если вектора линейно независимы, и они компланарны, то любые два из них неколлинеарны.
Обозначим эти вектора Если векторы
То есть векторы Определение 20 Упорядоченная совокупность линейно независимых векторов Определение 21 Если Теорема 10 Координаты вектора в базисе определяются единственным образом. Доказательство Допустим существует два разложения:
Тогда Так как Получили Теорема 11 При сложении векторов их координаты складываются. При умножении вектора на число его координаты домножаются на это число. Доказательство Рассмотрим два произвольных вектора
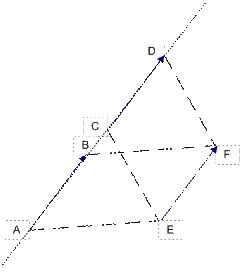
По определению координат вектора и единственности координат, координаты вектора Аналогично, если Координаты Теорема 12 Любые четыре вектора в пространстве линейно зависимы. Доказательство Если какие-то три вектора компланарны, то по доказанному ранее они линейно зависимы. Тогда и все четыре вектора линейно зависимы. Пусть никакие три вектора не компланарны. Отложим их от одной точки
Проведем через конец вектора Теорема 13 (о базисе в пространстве, на плоскости, на прямой) Верны следующие утверждения: 1) Любые три некомпланарных вектора образуют базис в пространстве. Доказательство Докажем первый пункт. По доказанному любые три некомпланарных вектора линейно независимы. Обозначим эти вектора Определение 22 Системой координат (аффинной системой координат) называется точка Определение 23 Координатами точки Замечание Если в пространстве даны две точки 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 с выбранным одним из двух направлений (от
с выбранным одним из двух направлений (от  к
к  или от
или от 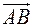 , а вектор с началом в
, а вектор с началом в  .
.
 равен сам себе
равен сам себе );
); , то вектор
, то вектор  );
); , то вектор
, то вектор 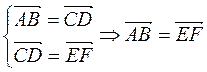 .
.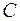 и
и  .
.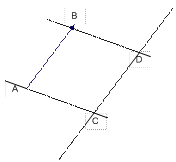
 является параллелограммом. Поэтому
является параллелограммом. Поэтому  . Имеем два вектора
. Имеем два вектора 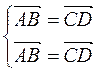 , значит по определению
, значит по определению 
 .
. , то
, то  .
. и
и  параллельны.
параллельны.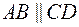 и
и  , то точки
, то точки  ,
,  лежат в одной плоскости.
лежат в одной плоскости. , т.е.
, т.е. 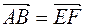 .
. и
и  .
.

 не лежит на одной прямой с остальными и
не лежит на одной прямой с остальными и 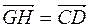 . Тогда
. Тогда , то
, то  ,
, , то
, то  .
.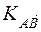 всех векторов, равных
всех векторов, равных  имеют общий вектор
имеют общий вектор  из
из  из
из  (так как
(так как  )
) (так как
(так как  )
) и
и  . Аналогично
. Аналогично 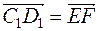 . Получаем, что
. Получаем, что  . Таким образом,
. Таким образом, 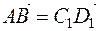 и
и  , то есть любой элемент из
, то есть любой элемент из  ,
, 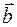 или
или 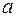 ,
,  .
.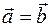 . Класс нулевых закрепленных векторов будем обозначать
. Класс нулевых закрепленных векторов будем обозначать  или
или 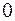 . Вместо записи
. Вместо записи 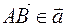 будем писать
будем писать  .
. называется вектор
называется вектор  .
.
 называется вектор
называется вектор  .
. точки
точки  – по разные.
– по разные.
 .
. , где
, где  ,
, 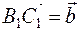 порождают один и тот же свободный вектор (класс равенства).
порождают один и тот же свободный вектор (класс равенства).
 ,
,  не лежат в одной плоскости. Тогда
не лежат в одной плоскости. Тогда  (см. доказательство теоремы 1). Значит векторы
(см. доказательство теоремы 1). Значит векторы  порождают один и тот же свободный вектор (класс равенства).
порождают один и тот же свободный вектор (класс равенства). коллинеарны.
коллинеарны.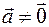 и
и 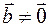 коллинеарны, то найдется число
коллинеарны, то найдется число  такое, что либо
такое, что либо  , либо
, либо  .
. . Так как
. Так как  и
и  , то возьмём
, то возьмём  , где берется знак «
, где берется знак «  », если
», если  и векторы
и векторы  порождают одинаковые классы равенства. Значит
порождают одинаковые классы равенства. Значит  задана операция сложения, если каждой упорядоченной паре из
задана операция сложения, если каждой упорядоченной паре из  и
и  из
из  ;
; из
из  ;
; , который обладает следующим свойством: для каждого
, который обладает следующим свойством: для каждого 
 ;
; существует элемент
существует элемент  такой, что
такой, что 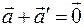 . Этот элемент называется обратным элементом к
. Этот элемент называется обратным элементом к  .
. выполняется
выполняется  .
. и любого
и любого  .
. .
. .
.

 .
.
 , равном расстоянию между точками
, равном расстоянию между точками 
 и
и  коллинеарны и направлены в одну сторону. Их модули равны соответственно
коллинеарны и направлены в одну сторону. Их модули равны соответственно 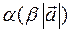 и
и  , т.е. равны друг другу. Значит векторы равны.
, т.е. равны друг другу. Значит векторы равны. с коэффициентами
с коэффициентами  называется сумма
называется сумма  .
. ) такие, что
) такие, что  .
. .
.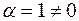 , тогда
, тогда  . Не все коэффициенты равны
. Не все коэффициенты равны  . Тогда линейная комбинация
. Тогда линейная комбинация  , но не все коэффициенты равны
, но не все коэффициенты равны  . Если
. Если  , не все равные
, не все равные  . Тогда линейная комбинация из всех векторов
. Тогда линейная комбинация из всех векторов  тоже равна
тоже равна 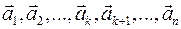 линейно зависимая, то и система векторов
линейно зависимая, то и система векторов  такое, что
такое, что 
 этих векторов может обращаться в ноль только если
этих векторов может обращаться в ноль только если 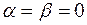 . Если это не так, то найдутся
. Если это не так, то найдутся  . Пусть
. Пусть  . Тогда
. Тогда  . Это значит, что они коллинеарны.
. Это значит, что они коллинеарны.
 ,
,  и
и  . Проведем через точку
. Проведем через точку  . Так как
. Так как  коллинеарен
коллинеарен  такое, что
такое, что  . Так как
. Так как 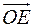 коллинеарен
коллинеарен 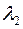 такое, что
такое, что  . Получим
. Получим  . Перенесем в одну сторону:
. Перенесем в одну сторону:  . Получим, что наши три вектора линейно зависимы, т.е. получим противоречие с предположением о компланарности.
. Получим, что наши три вектора линейно зависимы, т.е. получим противоречие с предположением о компланарности. такие, что
такие, что  и
и  . Пусть
. Пусть  . По определению операции сложения векторы
. По определению операции сложения векторы  ,
,  , отложенные из одной точки лежат в одной плоскости.
, отложенные из одной точки лежат в одной плоскости.
 называется базисом, если для любого вектора
называется базисом, если для любого вектора  существуют
существуют 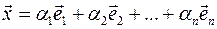 .
. - базис в пространстве
- базис в пространстве  в базисе
в базисе 
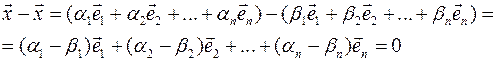
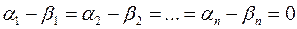
 .
. и
и  .
.  - координаты вектора
- координаты вектора  - координаты вектора
- координаты вектора  - базис.
- базис.
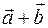 равны
равны  .
.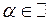 , то
, то 
 равны
равны  .
. .
.
 (точку
(точку  . Точки пересечения с прямыми, на которой лежат вектора
. Точки пересечения с прямыми, на которой лежат вектора 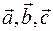 обозначим соответственно
обозначим соответственно  . Существуют ненулевые числа
. Существуют ненулевые числа  такие, что
такие, что  . При этом
. При этом  . Получили, что
. Получили, что 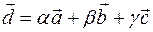 или
или  . Значит векторы
. Значит векторы 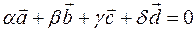 . Если
. Если 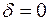 , то
, то  и должно выполняться
и должно выполняться  . Тогда
. Тогда  . Значит
. Значит  . Точка
. Точка  в системе координат
в системе координат  называются координаты вектора
называются координаты вектора  .
. , то координаты вектора
, то координаты вектора  в системе координат
в системе координат