Эксцентриситет и директриса
Пусть эллипс задан в канонической системе координат уравнением  , где , где 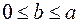 . Имеем . Имеем 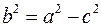 . Отсюда . Отсюда 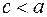 . .
Определение 62
Эксцентриситетом эллипса называется величина  . Легко видеть, что . Легко видеть, что  и если и если  (т.е. эллипс является окружностью), то (т.е. эллипс является окружностью), то  . Выразим . Выразим  через через 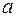 и и  . .

Рассмотрим прямую, перпендикулярную большей главной оси, проходящей через точку  , где , где  . Возьмем точку . Возьмем точку  на эллипсе, координаты точки на эллипсе, координаты точки  будем обозначать будем обозначать  . Тогда расстояние от точки . Тогда расстояние от точки  до прямой до прямой  равно равно  . Расстояние от точки . Расстояние от точки  до фокуса до фокуса  с координатами с координатами  равно равно 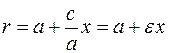 . Отношение расстояний от точки . Отношение расстояний от точки  до фокуса до фокуса  и от точки и от точки  до прямой до прямой  равно равно  . Это отношение постоянно, если . Это отношение постоянно, если  . Таким образом прямая, перпендикулярная большей главной оси, отстоящая от центра эллипса на расстояние . Таким образом прямая, перпендикулярная большей главной оси, отстоящая от центра эллипса на расстояние 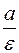 , лежащая по ту же сторону, что и фокус обладает тем свойством, что расстояние от любой точки эллипса до фокуса деленное на расстояние от этой точки до этой прямой постоянно и равно , лежащая по ту же сторону, что и фокус обладает тем свойством, что расстояние от любой точки эллипса до фокуса деленное на расстояние от этой точки до этой прямой постоянно и равно 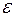 . Аналогично можно доказать, что отношение расстояний от точки эллипса до фокуса . Аналогично можно доказать, что отношение расстояний от точки эллипса до фокуса  и до прямой, перпендикулярной большей главной оси, проходящей через точку и до прямой, перпендикулярной большей главной оси, проходящей через точку  постоянно и равно постоянно и равно 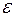 . .
Определение 63
Директрисой эллипса, отвечающей фокусу  , называется прямая, перпендикулярная большей главной оси такая, что отношение расстояний от точек эллипса до фокуса , называется прямая, перпендикулярная большей главной оси такая, что отношение расстояний от точек эллипса до фокуса  и до этой прямой постоянно и равно и до этой прямой постоянно и равно 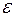 . .
Замечание
Если эллипса является окружностью, то директрис нет.
Замечание
Если эллипс не является окружностью, то для каждого эллипса существует единственная директриса.
Замечание
У эллипса, не являющегося окружностью, существует две директрисы.
Замечание
Из выведенных уравнений директрис видно, что директрисы не пересекают эллипс.
Если уравнение эллипса в канонической системе координат  , то уравнения директрис , то уравнения директрис  . .
Докажем, что если отношение расстояний от точки  до фокуса и его директрисы равно до фокуса и его директрисы равно 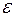 , то точка , то точка  принадлежит эллипсу. принадлежит эллипсу.
Для доказательства рассмотрим фокус  . Расстояние от . Расстояние от  до до  равно равно  , где , где  - координаты точки - координаты точки  . Расстояние от . Расстояние от  до директрисы равно до директрисы равно  . Так как отношение . Так как отношение 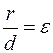 , то , то

То есть точка  принадлежит эллипсу. Обозначим расстояние от фокуса эллипса до его директрисы через принадлежит эллипсу. Обозначим расстояние от фокуса эллипса до его директрисы через  . Тогда . Тогда 
Пусть на плоскости задана прямая и точка. Тогда  найдется эллипс, для которого указанная точка будет фокусом, а указанная прямая будет директрисой, соответствующей этому фокусу. найдется эллипс, для которого указанная точка будет фокусом, а указанная прямая будет директрисой, соответствующей этому фокусу.
Выберем систему координат так: ось 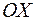 проходит через данную нам точку проходит через данную нам точку  и перпендикулярно данной прямой. Точку пересечения оси и перпендикулярно данной прямой. Точку пересечения оси 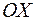 с данной прямой обозначим через с данной прямой обозначим через  . Отметим на оси . Отметим на оси 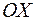 две точки две точки 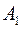 и и  такие, что такие, что  и и  и точка и точка 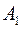 лежит между точками лежит между точками  и и  . Середину отрезка . Середину отрезка  обозначим через обозначим через   является началом координат. является началом координат.
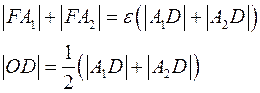
Заметим, что точка  лежит между точками лежит между точками  и и  , так как , так как 

Длина 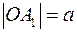 . Длина . Длина  . Найдем длину . Найдем длину 


 . Обозначим . Обозначим  . Для эллипса, заданного уравнением . Для эллипса, заданного уравнением  . Точка . Точка  совпадает с фокусом, а заданная прямая совпадает с директрисой этого фокуса, т.к. уравнение этой прямой совпадает с фокусом, а заданная прямая совпадает с директрисой этого фокуса, т.к. уравнение этой прямой  . .
Уравнение эллипса в полярных координатах
Пусть эллипс задан каноническим уравнением  . .
 - фокус с координатами - фокус с координатами  , его директриса – прямая, заданная уравнением , его директриса – прямая, заданная уравнением  , точка , точка  принадлежит эллипсу тогда и только тогда, когда принадлежит эллипсу тогда и только тогда, когда 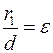 , где , где  , ,  - расстояние от точки - расстояние от точки  до прямой до прямой  . Выберем полярную ось через точки . Выберем полярную ось через точки  и и  . Тогда расстояние от точки . Тогда расстояние от точки  до начала полярной системы координат до начала полярной системы координат  . Вектор . Вектор  составляет угол составляет угол 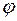 с полярной осью. Расстояние от точки с полярной осью. Расстояние от точки  до директрисы равно до директрисы равно  , где , где  - расстояние от фокуса до директрисы. Точка - расстояние от фокуса до директрисы. Точка  принадлежит эллипсу тогда и только тогда, когда принадлежит эллипсу тогда и только тогда, когда  . .

Гипербола
Определение 64
Гиперболой называется множество точек плоскости таких, что абсолютная величина разности расстояний от которых до двух фиксированных точек  и и  , называемых фокусами, постоянна. Обозначим указанную разность через , называемых фокусами, постоянна. Обозначим указанную разность через  , а расстояние между фокусами через , а расстояние между фокусами через  . .
Замечание
Если  и и  совпадают и совпадают и  , то точек, удовлетворяющих такому условию на плоскости нет. Если , то точек, удовлетворяющих такому условию на плоскости нет. Если  и и  совпадают и совпадают и  , то любая точка плоскости удовлетворяет указанному условию. Поэтому будем считать, что фокусы , то любая точка плоскости удовлетворяет указанному условию. Поэтому будем считать, что фокусы  и и  являются разными точками. являются разными точками.
Замечание
Обозначим расстояние от точки  до до  через через  , а расстояние от , а расстояние от  до до  через через  . Так как . Так как  и и  , то , то

Введем систему координат следующим образом: ось 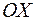 проведем через фокусы проведем через фокусы  и и  , начало координат возьмем в центре отрезка , начало координат возьмем в центре отрезка  . Ось . Ось 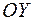 проведем перпендикулярно оси проведем перпендикулярно оси 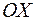 через начало координат. Тогда координаты точки через начало координат. Тогда координаты точки  , точки , точки  . Пусть координаты . Пусть координаты  . Тогда . Тогда  . .  принадлежит гиперболе тогда и только тогда, когда принадлежит гиперболе тогда и только тогда, когда
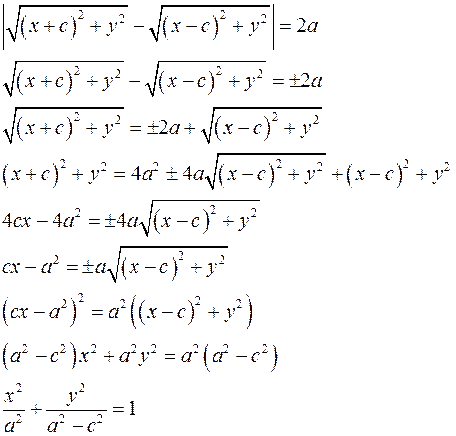
Обозначим величину  , ,  . Тогда уравнение примет вид . Тогда уравнение примет вид  . Проверим, что каждая точка, удовлетворяющая уравнению . Проверим, что каждая точка, удовлетворяющая уравнению  принадлежит гиперболе. Пусть координаты точки принадлежит гиперболе. Пусть координаты точки  удовлетворяют уравнению удовлетворяют уравнению  . Тогда . Тогда 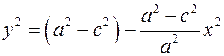 . Расстояние от . Расстояние от  до до  равно равно 
Так как из уравнения  следует, что следует, что  либо либо  либо либо  , то , то

Расстояние от  до до  равно равно
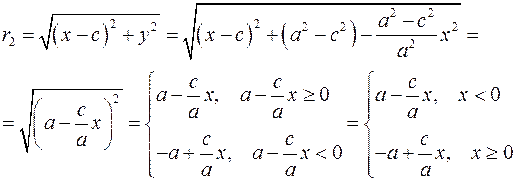
 . Получили, что . Получили, что  принадлежит гиперболе. принадлежит гиперболе.
Определение 65
Уравнение вида  , где , где  называется каноническим уравнением гиперболы, а система координат, в которой гипербола имеет каноническое уравнение называется канонической системой координат. называется каноническим уравнением гиперболы, а система координат, в которой гипербола имеет каноническое уравнение называется канонической системой координат.
Свойства гиперболы
Пусть в канонической системе координат гипербола имеет уравнение  . .
1) Гипербола обладает двумя осями симметрии (главные оси). Одна ось симметрии – ось  , другая – ось , другая – ось  . Одна из осей симметрии – фокальная ось (ось, проходящая через фокусы). . Одна из осей симметрии – фокальная ось (ось, проходящая через фокусы).
2) Точка пересечения осей симметрии является точкой симметрии гиперболы.
3) Из уравнения  получаем, что в полосе получаем, что в полосе  точек гиперболы нет. точек гиперболы нет.
4) Из уравнения  следует, что следует, что  , т.е. , т.е.  . Значит гипербола лежит между прямыми . Значит гипербола лежит между прямыми  и и  , как показано на рисунке: , как показано на рисунке:

Определение 66
Точки пересечения фокальной оси с гиперболой называются вершинами гиперболы.
Прямые  и и  являются асимптотами гиперболы. являются асимптотами гиперболы.
Рассмотрим прямую 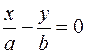 и часть гиперболы и часть гиперболы  , где , где 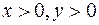 . .
Тогда для прямой  , для гиперболы , для гиперболы 
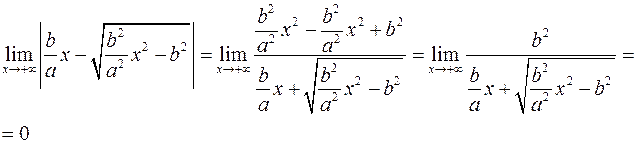
Аналогично для остальных частей гиперболы (  ) и прямой ) и прямой  . .
Определение 67
Число  называется эксцентриситетом гиперболы. Так как называется эксцентриситетом гиперболы. Так как  , то , то  . .
Рассмотрим прямую  , где , где 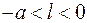 Расстояние от точки Расстояние от точки  до этой прямой равно до этой прямой равно  . Расстояние от точки . Расстояние от точки  до фокуса до фокуса  равно равно  и до точек гиперболы и до точек гиперболы 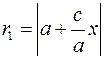 . Отношение расстояния от точки гиперболы до фокуса и до прямой . Отношение расстояния от точки гиперболы до фокуса и до прямой  равно равно 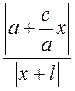 . Это отношение постоянно, когда . Это отношение постоянно, когда  . Таким образом отношение расстояний от точек гиперболы до фокуса . Таким образом отношение расстояний от точек гиперболы до фокуса  и от точек гиперболы до прямой и от точек гиперболы до прямой  постоянно и равно постоянно и равно  . .
Определение 68
Прямая, перпендикулярная фокальной оси, пересекающая отрезок между фокусами  и и  , отстоящая от фокуса , отстоящая от фокуса  на расстояние на расстояние  называется директрисой гиперболы для фокуса называется директрисой гиперболы для фокуса  . Директриса фокуса . Директриса фокуса  в канонической системе координат имеет уравнение в канонической системе координат имеет уравнение  . Директриса фокуса . Директриса фокуса  в канонической системе координат имеет уравнение в канонической системе координат имеет уравнение  . .
Проверим, что точка, для которой отношение расстояний до фокуса и до директрисы этого фокуса равно 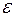 принадлежит гиперболе. принадлежит гиперболе.
Пусть точка имеет координаты  . Расстояние до фокуса . Расстояние до фокуса  равно равно  . Расстояние до директрисы . Расстояние до директрисы  равно равно  . Так как . Так как 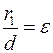 , то , то

Получили, что точка  принадлежит гиперболе. Аналогично доказывается для второго фокуса. принадлежит гиперболе. Аналогично доказывается для второго фокуса.
Пусть задана прямая  , точка , точка  и и 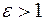 . Тогда найдется гипербола, для которой точка . Тогда найдется гипербола, для которой точка  является фокусом, а прямая является фокусом, а прямая  директрисой относительно этого фокуса, директрисой относительно этого фокуса, 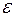 является эксцентриситетом гиперболы. Построим гиперболу. Для этого выберем систему координат. Ось является эксцентриситетом гиперболы. Построим гиперболу. Для этого выберем систему координат. Ось 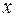 проведем через проведем через  перпендикулярно прямой перпендикулярно прямой  . Точку пересечения оси . Точку пересечения оси 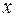 и прямой и прямой  обозначим через обозначим через  . Возьмем точку . Возьмем точку 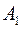 на отрезке на отрезке  так, чтобы так, чтобы  и точку и точку  на оси на оси 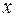 такую, что такую, что  . Точка . Точка  лежит по другую сторону от лежит по другую сторону от  , чем точка , чем точка 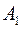 . Выберем началом системы координат середину отрезка . Выберем началом системы координат середину отрезка  . Обозначим начало координат . Обозначим начало координат  . Очевидно, что точка . Очевидно, что точка  лежит по одну сторону от прямой лежит по одну сторону от прямой  , что и точка , что и точка  (так как (так как 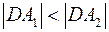 ). Обозначим ). Обозначим  , ,  . Направление оси . Направление оси 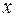 выберем так, чтобы точка выберем так, чтобы точка  имели координаты имели координаты  . .
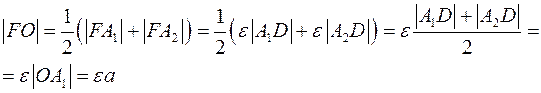
Получили, что  или или  . Найдем . Найдем  : :

Получили, что уравнение прямой  имеет вид имеет вид  . Для гиперболы . Для гиперболы  точка точка  является фокусом, а прямая является фокусом, а прямая  является директрисой, соответствующей этому фокусу. является директрисой, соответствующей этому фокусу.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , где
, где 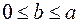 . Имеем
. Имеем 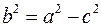 . Отсюда
. Отсюда 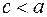 .
. . Легко видеть, что
. Легко видеть, что  и если
и если  (т.е. эллипс является окружностью), то
(т.е. эллипс является окружностью), то  . Выразим
. Выразим 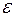 через
через 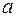 и
и  .
.
 , где
, где  . Возьмем точку
. Возьмем точку  на эллипсе, координаты точки
на эллипсе, координаты точки  . Тогда расстояние от точки
. Тогда расстояние от точки  равно
равно  . Расстояние от точки
. Расстояние от точки  с координатами
с координатами  равно
равно 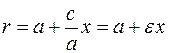 . Отношение расстояний от точки
. Отношение расстояний от точки  . Это отношение постоянно, если
. Это отношение постоянно, если  . Таким образом прямая, перпендикулярная большей главной оси, отстоящая от центра эллипса на расстояние
. Таким образом прямая, перпендикулярная большей главной оси, отстоящая от центра эллипса на расстояние 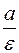 , лежащая по ту же сторону, что и фокус обладает тем свойством, что расстояние от любой точки эллипса до фокуса деленное на расстояние от этой точки до этой прямой постоянно и равно
, лежащая по ту же сторону, что и фокус обладает тем свойством, что расстояние от любой точки эллипса до фокуса деленное на расстояние от этой точки до этой прямой постоянно и равно  и до прямой, перпендикулярной большей главной оси, проходящей через точку
и до прямой, перпендикулярной большей главной оси, проходящей через точку  постоянно и равно
постоянно и равно  , называется прямая, перпендикулярная большей главной оси такая, что отношение расстояний от точек эллипса до фокуса
, называется прямая, перпендикулярная большей главной оси такая, что отношение расстояний от точек эллипса до фокуса  .
. , где
, где  . Так как отношение
. Так как отношение 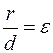 , то
, то
 . Тогда
. Тогда 
 найдется эллипс, для которого указанная точка будет фокусом, а указанная прямая будет директрисой, соответствующей этому фокусу.
найдется эллипс, для которого указанная точка будет фокусом, а указанная прямая будет директрисой, соответствующей этому фокусу. проходит через данную нам точку
проходит через данную нам точку  . Отметим на оси
. Отметим на оси 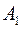 и
и  такие, что
такие, что  и
и  и точка
и точка  обозначим через
обозначим через 
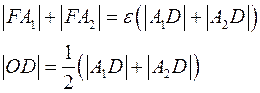


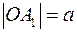 . Длина
. Длина  . Найдем длину
. Найдем длину 


 . Обозначим
. Обозначим  . Для эллипса, заданного уравнением
. Для эллипса, заданного уравнением  . Точка
. Точка  .
. , точка
, точка 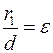 , где
, где  ,
,  - расстояние от точки
- расстояние от точки  . Вектор
. Вектор  составляет угол
составляет угол 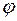 с полярной осью. Расстояние от точки
с полярной осью. Расстояние от точки  , где
, где  .
.
 , называемых фокусами, постоянна. Обозначим указанную разность через
, называемых фокусами, постоянна. Обозначим указанную разность через  , а расстояние между фокусами через
, а расстояние между фокусами через  .
. , то точек, удовлетворяющих такому условию на плоскости нет. Если
, то точек, удовлетворяющих такому условию на плоскости нет. Если  , то любая точка плоскости удовлетворяет указанному условию. Поэтому будем считать, что фокусы
, то любая точка плоскости удовлетворяет указанному условию. Поэтому будем считать, что фокусы  , а расстояние от
, а расстояние от  . Так как
. Так как  и
и  , то
, то
 . Ось
. Ось  проведем перпендикулярно оси
проведем перпендикулярно оси  , точки
, точки  . Тогда
. Тогда  .
. 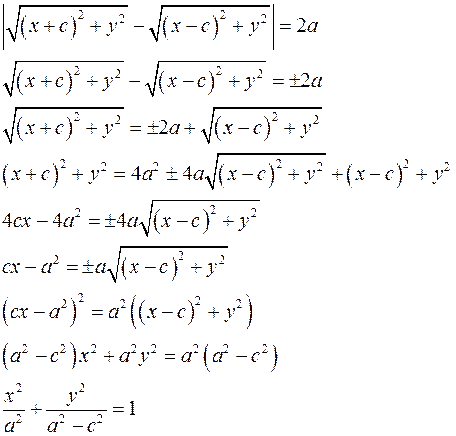
 ,
,  . Тогда уравнение примет вид
. Тогда уравнение примет вид  . Проверим, что каждая точка, удовлетворяющая уравнению
. Проверим, что каждая точка, удовлетворяющая уравнению 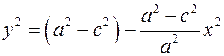 . Расстояние от
. Расстояние от 
 либо
либо 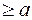 либо
либо  , то
, то
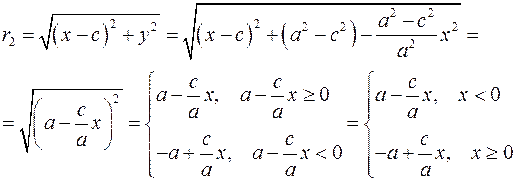
 . Получили, что
. Получили, что  называется каноническим уравнением гиперболы, а система координат, в которой гипербола имеет каноническое уравнение называется канонической системой координат.
называется каноническим уравнением гиперболы, а система координат, в которой гипербола имеет каноническое уравнение называется канонической системой координат. , другая – ось
, другая – ось  . Одна из осей симметрии – фокальная ось (ось, проходящая через фокусы).
. Одна из осей симметрии – фокальная ось (ось, проходящая через фокусы). точек гиперболы нет.
точек гиперболы нет. , т.е.
, т.е.  . Значит гипербола лежит между прямыми
. Значит гипербола лежит между прямыми  и
и  , как показано на рисунке:
, как показано на рисунке:
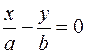 и
и  являются асимптотами гиперболы.
являются асимптотами гиперболы.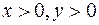 .
. , для гиперболы
, для гиперболы 
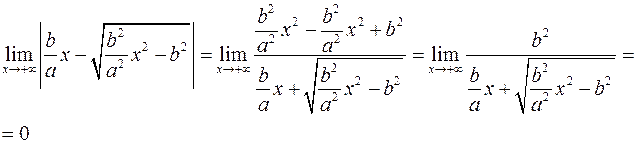
 ) и прямой
) и прямой  называется эксцентриситетом гиперболы. Так как
называется эксцентриситетом гиперболы. Так как  , то
, то  .
. , где
, где 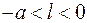 Расстояние от точки
Расстояние от точки  . Расстояние от точки
. Расстояние от точки 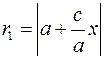 . Отношение расстояния от точки гиперболы до фокуса и до прямой
. Отношение расстояния от точки гиперболы до фокуса и до прямой 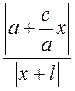 . Это отношение постоянно, когда
. Это отношение постоянно, когда  . Таким образом отношение расстояний от точек гиперболы до фокуса
. Таким образом отношение расстояний от точек гиперболы до фокуса  называется директрисой гиперболы для фокуса
называется директрисой гиперболы для фокуса  в канонической системе координат имеет уравнение
в канонической системе координат имеет уравнение  . Так как
. Так как 
 и
и 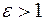 . Тогда найдется гипербола, для которой точка
. Тогда найдется гипербола, для которой точка  так, чтобы
так, чтобы  на оси
на оси 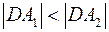 ). Обозначим
). Обозначим  ,
,  . Направление оси
. Направление оси 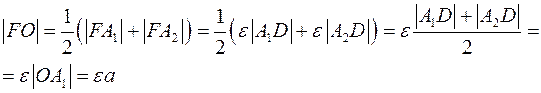
 или
или  :
:
 точка
точка