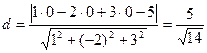|
|
Глава 10 Поверхности второго порядка.Основные типы поверхностей второго порядка. Определение 1: Цилиндрической поверхностью называется поверхность описываемая прямой, остающейся параллельно некоторой данной прямой и пересекающей заданную линию L.
Пример цилиндрической поверхности круговой цилиндр имеет уравнение: x2+y2=r2 Образующая параллельна оси ОZ. В качестве второго примера рассмотрим поверхность: у=ех Образующая этой поверхности параллельна оси OZ, а направляющая линия расположена в плоскости ХОУ и представляет собой экспоненту у=ех.
Определение 2: Конической поверхностью называется поверхность описываемая прямой проходящей через данную точку - вершина конуса – и пересекающую данную линию – направляющую конуса. Прямая называется образующей конуса.
Простейшее уравнение кругового конуса: х2+у2-z2=0 Вершина конуса находится в начале координат. Рассмотрим некоторые типы поверхностей, которые носят общее название – поверхности вращения.
Эллипсоид вращения.
Поверхность получается вращением эллипса Однополосный гиперболоид вращения
Поверхность получается вращением гиперболы Двуполостный гиперболоид вращения.
Поверхность получена вращением гиперболы
Параболоид вращения.
х2+у2=2рz
Поверхность получается вращением параболы у2=2рz вокруг оси OZ.
Рассмотренные поверхности вращения, легко обобщаются в эллиптические поверхности при замене окружности эллипсом. Тогда имеем. Эллипсоид
Однополосный гиперболоид
Двуполостный гиперболоид
Эллиптический параболоид
Конус второго порядка
Гиперболический параболоид
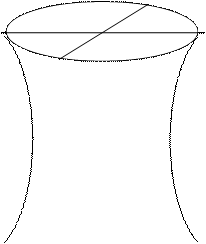
Цилиндры второго порядка а) Эллиптический.
б) Параболический
в) Гиперболический
0 y
x
Рис 10.1.
z
x
Рис 10.2
x
Рис 10.3

X
Рис. 10.4
0 1
Рис 10.5
z
Рис. 10.6

x
Рис. 10.7
z
0 y
x
Рис. 10.8
0 y
x
Рис. 10.9
Рассмотрим общее уравнение поверхности второго порядка, которое преобразуется с помощью формул параллельного переноса системы координат одному из уравнений поверхности второго порядка. Ax2+By2+Cz2+2Dx+2Ey+2Fz+G=0 Для преобразования этого уравнения будем использовать формулы параллельного переноса: x=x0+x1 y=y0+y1 z=z0+z1 где О1(х0,у0,z0) координаты нового начала координат х1, у1, z1 новые координаты. Рассмотрим пример преобразования общего уравнения поверхности.
Пример 1: Определить тип поверхности и сделать её схематический чертёж. x2+y2-z2+2x-4y+6z-6=0 Решение: Воспользуемся формулами параллельного переноса.
(х0+х1)2+(у0+у1)2-(z0+z1)2+2(x0+x1)-4(y0+y1)+6(z0+z1)-6=0
Преобразуем это уравнение
Найдём координаты нового начала координат, приравняв к нулю коэффициенты при х1,у1,z1, получим:
Тогда можно определить свободный член
В новой системе координат уравнение получим в виде.
Полученное уравнение представляет собой двуполостный гиперболоид вращения относительно оси О1Z1. Изобразим его схематически. (Рис. 10.10)

01
x1
x
Рис. 10.10
Приложение Разбор типовой аудиторной контрольной работы
В этом приложении приведём разбор аудиторной контрольной работы, которая даётся студентам первого курса и является обязательным контрольным мероприятием. Контрольная состоит из 5 задач. Задача 1: Решить неравенство
Решение: Вычислим определитель третьего порядка раскрываем его по первой строке.
Ответ:
Задача 2: Даны точки А(-1;1;6), В(0;4;-1), С(3;1;4), D(-1;6;1). Найти: а) угол между векторами б) площадь треугольника АВС с) Объём пирамиды АВСD.
Решение:
а) Для нахождения угла между векторами
Далее используем формулу нахождения угла между векторами заданными своими проекциями. Обозначим искомый угол
Зная б) Для нахождения площади треугольника АВС найдём проекции векторов
Известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах. Тогда площадь треугольника АВС будет равна половине площади параллелограмма. Таким образом.
Найдём векторное произведение векторов
Таким образом, проекции вектора векторного произведения будут: (-6: -26: -12) Тогда легко находим модуль векторного произведения:
Отсюда: в) Для нахождения объёма пирамиды АВСD необходимо знать проекции векторов
из векторной алгебры известно, что объем пирамиды может быть вычислен с помощью смешанного произведения векторов образующих пирамиду
Найдём смешанное произведение векторов заданных своими проекциями тогда искомый объем пирамиды
Задача 3: Найти вектор причем проекции векторов
Решение: Обозначим проекции вектора Зная проекции векторов
используя заданные начальные условия, получим систему с тремя неизвестными:
Решая эту систему, получаем: x=4; у=-2; z=2; таким образом, искомый вектор
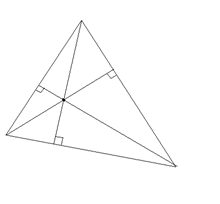
Задача 4: Даны две вершины треугольника А(-6;2) В(2;-2) и точка Н(1;2) пересечения его высот. Вычислить координаты третьей вершины С.
Решение
Найдём уравнение стороны треугольника АС используя уравнение прямой проходящей через заданную точку перпендикулярно заданному вектору: А(х-х0)+В(у-у0)=0. В качестве вектора перпендикулярного АС возьмем вектор
В качестве точки, через которую проходит прямая координаты точки А, тогда имеем уравнение АС. -1(х+6)+4(у-2)=0 -х-6+4у-8=0 -х+4у-14=0 х-4у+14=0 Аналогично найдём уравнение стороны треугольника ВС. Вектор перпендикулярный к ВС вектор Точка, через которую проходит ВС – точка В (2;-2) 7(х-2)+0(у+2)=0 7х-14=0 х-2=0 Имеем уравнения двух прямых, которые пересекаются в точке С. Для нахождения координат точки С решим систему уравнений
таким образом некоторые координаты С(2;4)
Задача 5: Вычислить расстояние между параллельными плоскостями заданными уравнениями x-2у+3z=0 и х-2у+3z-5=0 Решение: Обозначим Р1 плоскость х-2у+3z=0, а Р2 плоскость х-2у+3z-5=0. Найдём точку припадающую плоскости Р1. Для этого положим две координаты х=0 и у=0, тогда имеем 0-2*0+3z=0 => z=0. То есть плоскость Р1 проходит через начало координат, таким образом точка (0,0,0) принадлежит плоскости Р1. Найдём расстояние от этой точки до плоскости Р2 . Это и будет искомое расстояние между параллельными плоскостями Р1 и Р2. Для этого воспользуемся формулой расстояния от заданной точки до заданной плоскости:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
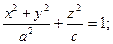
 вокруг оси OZ.
вокруг оси OZ.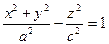 ;
; вокруг оси OZ.
вокруг оси OZ.
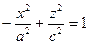 вокруг оси OZ.
вокруг оси OZ. (Рис. 10.1)
(Рис. 10.1)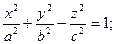 (Рис. 10.2)
(Рис. 10.2)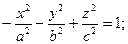 (Рис. 10.3)
(Рис. 10.3)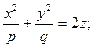 (Рис. 10.4)
(Рис. 10.4)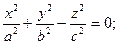 (Рис. 10.5)
(Рис. 10.5)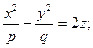 (Рис. 10.6)
(Рис. 10.6) (Рис. 10.7)
(Рис. 10.7)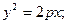 (Рис. 10.8)
(Рис. 10.8)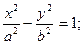 (Рис. 10.9)
(Рис. 10.9) z
z 




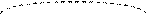 y
y 
 z
z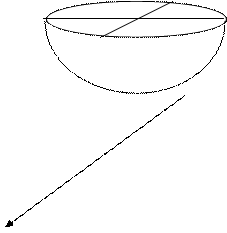


 0 y
0 y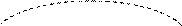



 z
z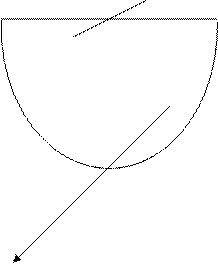
 0 y
0 y z
z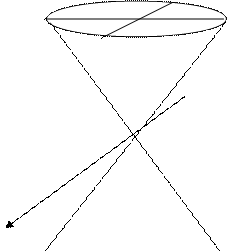




 0 y
0 y
 x
x  z
z

 y
y

 z
z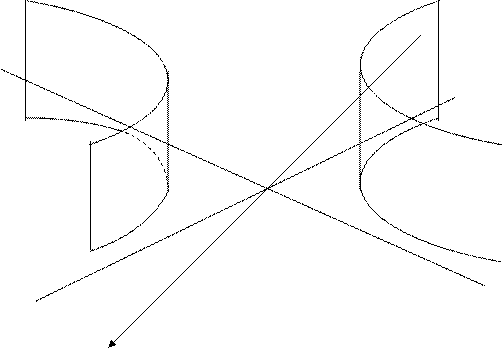


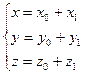

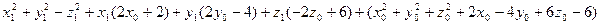
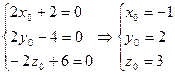

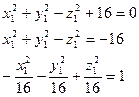





 y1
y1


 y
y

 0
0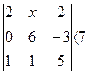
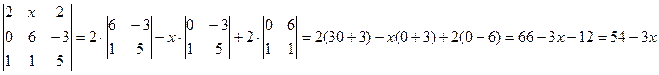 тогда неравенство преобразуется к виду
тогда неравенство преобразуется к виду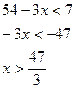
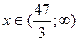
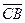 и
и 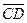
 ;
; 
 .
.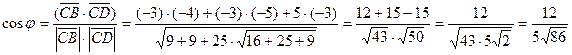
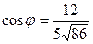 по таблицам находим угол
по таблицам находим угол 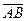 и
и 
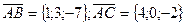
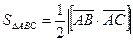


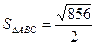 ед. кв.
ед. кв.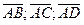
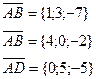
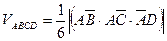
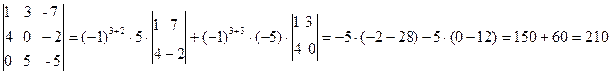
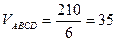 куб. ед.
куб. ед.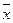 , если известно, что
, если известно, что 
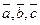 заданы:
заданы:

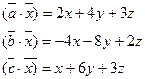
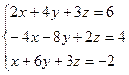
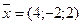
 , лежащий на высоте треугольника, проведённая из вершины В к стороне АС
, лежащий на высоте треугольника, проведённая из вершины В к стороне АС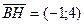
 :
: