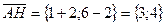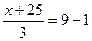|
|
Условие параллельности и перпендикулярности прямых. Расстояние от точки до прямой.Пусть заданы две неперпендикулярные прямые. Углом между ними будем называть меньший из углов образованных этими прямыми. В случае если прямые заданы уравнениями.
В случае если прямые заданы общими уравнениями. А1х+В1у+С1=0 А2х+В2у+С2=0
В случае если прямые заданы уравнениями с угловыми коэффициентами: Рассмотрим теперь случай, когда прямые параллельны. Для различных уравнений имеют различные условия параллельности: 1. 2. 3. Условие перпендикулярности прямых также различны для различных уравнений: 1. 2. 3. Если задана прямая общим уравнением Ах+Ву+С=0 и некоторая точка М(х1,у1) не лежащая на прямой, то расстояние от этой точки до заданной прямой определяется формулой: Рассмотрим примеры решения задач по теме главы 4.
Пример 1: Даны вершины треугольника А(3,2); В(-1,5); С(1,-2). Составить уравнение высоты ВD и найти её длину. Решение: Сделаем схематический чертёж (Рис 4.7)
В
А D С Рис. 4.7 Найдём проекции вектора
Имеем вектор
–2(х-(х-1)+(-4)(у-5)=0 При решении задач по аналитической геометрии все полученные уравнения будем преобразовывать к общему уравнению прямой. Тогда в нашем случае получим: -2х-2-4у+20=0 -2х-4у+18=0 или 2х+4у-18=0 полученное уравнение можно поделить на 2 х+2у-9=0 – это и есть искомое уравнение в виде общего уравнения прямой на плоскости. Для нахождения длины высоты BD воспользуемся формулой расстояния от точки до заданной прямой. Но для этого необходимо найти уравнение прямой АС. Найдём уравнение прямой АС, как уравнение прямой, проходящей через 2 заданные точки А и С.
Пусть А – первая точка, С – вторая точка
преобразуем полученное уравнение к общему виду.
Полученное уравнение и будет уравнением АС в общем виде. Тогда
Пример 2: Даны вершины треугольника А(3,2);В(-1,5);С(1,-2). Составить уравнение медианы ВК и найти её длину. Решение: Сделаем схематический чертёж (Рис 4.8)
В
А
К С Рис 4.8
Найдём координаты точки К, как середины отрезка АС.
Полученное уравнение – уравнение медианы. Длину медианы ВК найдём как расстояние между двумя точками на плоскости, заданными своими координатами.
Пример 3: Даны вершины треугольника А(3,2); В(-1,5); С(-5,-3).Составить уравнение биссектрисы ВN и найти её длину. Решение: Сделаем схематический чертёж (Рис. 4.9) В
А N С
Рис. 4.9
Для нахождения координат точки N воспользуемся теоремой о биссектрисе, известно из средней школы, что биссектриса делит противоположную сторону треугольника в том отношении, как относятся соответствующие прилегающие стороны таким образом:
найдём длины сторон треугольника
обозначим отношение Далее используем формулу деления отрезка в заданном отношении.
таким образом, координаты точки Используя уравнение прямой проходящей через 2 заданные точки, получим:
уравнение биссектрисы ВN. Для нахождения длины биссектрисы BN воспользуемся формулой:
Пример4 Составить уравнение прямой, проходящей через точку А(2;-3) перпендикулярную прямой, заданной уравнением 3х-4у+2=0 Решение Сделаем схематический чертёж (Рис 4.10)
Рис. 4.10
Из уравнения заданной прямой определяем проекции вектора
Преобразуем полученное уравнение к общему виду. (х-2)(-4)=(у+3)3 -4х+8=3у+9 -4х-3у+8-9=0 -4х-3у-1=0 4х+3у+1=0 – искомая прямая
Пример 5: На прямой 2х+у-5=0 найти точку С, равноудалённую от точки А(5;5), В(-2;4) Решение: Сделаем схематический чертёж (Рис. 4.11)
С(хс,ус) Рис. 4.11
По условию задачи расстояние от точек А и В до прямой одинаковы, то есть
Таким образом координаты искомой точки С(2,1) Пример 6: Даны две стороны параллелограмма 2х-3у-1=0, 3х-4у-2=0 и точка Е(3,2) пересечение его диагоналей. Составить уравнение двух других его сторон. Решение: Сделаем схематический чертёж (Рис 4.12)
Е(3,2)
Рис. 4.12 Две заданные стороны параллелограмма пересекаются в точке А, поэтому решая совместно систему уравнений найдём координаты точки А.
А(2,1) Используя свойства параллелограмма, что диагонали в точке пересечения делятся пополам найдём координаты точки С
С(4,3)
Зная координаты точки С легко найти уравнения сторон параллелограмма ВС и DC. Ищем уравнение ВС в виде 3х-4у-2=0, то используя условие параллельности двух прямых, получим:
тогда можно принять А2=3, В2=-4 и уравнение ВС 3(х-4)+(-4)(у-3)=0 3х-12-4у+12=0 3х-4у=0 Аналогично используя параллельность сторон параллелограмма CD и АВ: 2х-3у-1=0, получим уравнение CD в виде: 2(х-4)+(-3)(у-3)=0 2х-8-3у+9=0 2х-3у+1=0 Пример 7: Найти точку симметричную точке Р (10,21) относительно прямой 2х+5у-38=0. Решение: Сделаем схематический чертёж (Рис. 4.13)
Рис. 4.13 Найдём уравнение прямой, проходящей через точку Р. перпендикулярную заданной прямой. Из уравнения заданной прямой 2х+5у-38=0 легко определяются проекции вектора перпендикулярного заданной прямой
преобразуем уравнение к общему виду. 5(х-10)=2(у-21) 5х-50-2у+42=0 5х-2у-8=0 Найдём координаты точки К, как точки пересечения прямых 2х+5у-38=0 и 5х-2у-8=0, решая совместно систему двух уравнений с двумя неизвестными.
таким образом, координаты точки К(4,6) зная координаты точки К и точки Р и используя то, что точка К является серединой отрезка РР/ найдём координаты точки Р/
искомая точка Р/ имеет координаты Р/(-2,-9).
Пример 8: Даны вершина треугольника А(-2,3) его медианы 5х-2у-10=0 и 7х+5у-27=0. составить уравнение сторон треугольника. Решение: Прежде всего убедимся, что заданная вершина треугольника А(-2,3) не лежит ни на одной из заданных медиан. Для этого будем подставлять координаты точек А в уравнение медиан и, если они не обращаются в тождества, это означает, что точка не лежит на прямой. Рассмотрим медианы
Рис. 4.14 Найдём координаты точки В(хв,ув) Так как точка В лежит на медиане ВК, то она обращает уравнение ВК в тождество 5хв-2ув-10=0 Выразим координаты точки М, как серидины отрезка АВ через координаты точек А и В.
Подставляя координаты точки М в уравнение медианы СМ, получим второе уравнение:
получим систему двух уравнений с двумя неизвестными.
Таким образом, точка В имеет координаты В(4;5) Зная координаты точек А и В запишем уравнение сторон треугольника АВ, как прямой проходящей через 2 заданные точки.
Координаты точки С, находим аналогично. Точка С(хс,ус) лежит на медиане СМ 7хс+5ус-27=0 Точка К лежит на медиане ВК
Получим систему уравнений
Таким образом точка С имеет координаты С(6;-3). Зная координаты точек А и С находим уравнение сторон АС
Зная координаты точек В и С найдём уравнение сторон ВС
Таким образом мы нашли уравнение всех трёх сторон треугольника:
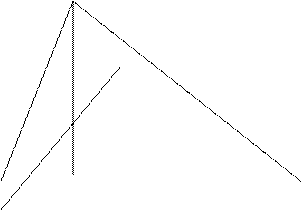
Пример 9: Даны две вершины треугольника А(-2;2), В(10;8) и точка пересечения его высот Н(1;6). Найти координаты третьей вершины треугольника. Решение: Сделаем схематический чертёж к задаче (Рис 4.15)
А
Н
Рис. 4.15
Используя уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору, найдём уравнение сторон АС и ВС. Для нахождения уравнения АС найдём вектор
тогда уравнение АС
Для нахождения уравнения ВС, найдём вектор
тогда уравнение ВС
Стороны АС и ВС пересекаются в точке С, поэтому для нахождения её координат рассмотрим систему уравнений, в которую входят уравнения прямой АС и прямой ВС.
Таким образом координаты точки С(-6;11)
Задачи для самостоятельного решения 1. Составить уравнение прямой проходящей через точку А(2;-3) перпендикулярную прямой, заданной уравнением 2. Найти расстояние от точки А(1;2) до прямой 4х+3у-5=0 3. Найти координаты точки В симметричной точке А(1;3) относительно прямой 2х+у-10=0 4. Через точку пересечения прямых х-2у-5=0 и 2х-3у-8=0 провести прямую параллельную прямой 3х-2у+2=0 5. Стороны треугольника выражаются уравнениями х+3у-2=0; 2х+у+5=0; 3х-4=0. найти уравнения высот треугольника. 6. Вершины треугольника А(2;1), В(0;7), С(-4;-1). Найти уравнения медиан треугольника и координаты точки их пересечения. 7. Найти уравнение прямой, проходящей через начало координат и через точку пересечения медиан треугольника, стороны которого выражаются уравнениями х-у-4=0, 2х-11у+37=0, 2х+7у-17=0 8. Найти координаты точки равноудалённой от трёх точек А(2;3), В(4;2), С(-1;0). 9. Даны две вершины равностороннего треугольника АВС; А(2;1), и В(2;5). Найти координаты третьей вершины С. 10. На прямой х+3у=0 найти точку, равноудалённую от начала координат и от прямой х+3у-2=0. 11. Найти расстояние между параллельными прямыми 3х+4у-15=0, 3х+4у+20=0. 12. Найти уравнения биссектрис углов образуемых прямыми 3х+4у-9=0 и 12х+9у-8=0. Проверить, что эти биссектрисы перпендикулярны друг другу. 13. Даны центр квадрата С(-1;0) и уравнение стороны х+3у-5=0. найти уравнения трёх его других сторон. 14. Найти уравнение биссектрисы внешнего угла А треугольника с вершинами А(0;0), В(3;0), С(0;7). 15. В прямоугольном равнобедренном треугольнике даны уравнение катета у=2х и середина гипотенузы К(2;4). Найти уравнения двух других сторон треугольника. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
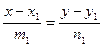 и
и 
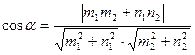




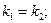

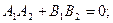

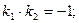






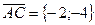


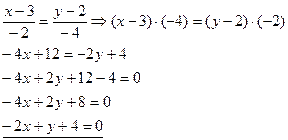



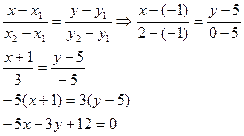 Найдём уравнение ВК, как прямой, проходящей через 2 точки.
Найдём уравнение ВК, как прямой, проходящей через 2 точки.
 длина медианы ВК
длина медианы ВК

 и
и 

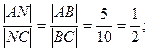

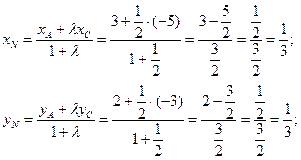




 А(2;-3)
А(2;-3)

 перпендикулярного заданной прямой
перпендикулярного заданной прямой  . По условию задачи этот вектор параллелен искомой прямой. Тогда воспользуемся уравнением прямой проходящей через заданную точку параллельно заданному вектору.
. По условию задачи этот вектор параллелен искомой прямой. Тогда воспользуемся уравнением прямой проходящей через заданную точку параллельно заданному вектору.
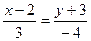
 А
А В
В



 . Обозначив координаты точки С(хс,ус), запишем первое условие:
. Обозначив координаты точки С(хс,ус), запишем первое условие:



 В С
В С
 А D
А D
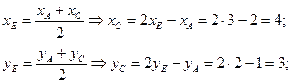
 . Так как стороны ВС и AD параллельны и уравнение стороны AD известно:
. Так как стороны ВС и AD параллельны и уравнение стороны AD известно: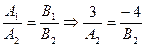



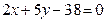




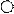
 , этот вектор
, этот вектор  . Тогда используем уравнение прямой, проходящей через заданную точку параллельно заданному вектору, причём в качестве такого вектора берём вектор
. Тогда используем уравнение прямой, проходящей через заданную точку параллельно заданному вектору, причём в качестве такого вектора берём вектор 
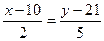



 Таким образом точка А не лежит на заданных медианах, то есть в треугольнике АВС нам заданны уравнения медиан ВК и СМ. сделаем схематический чертёж. (Рис. 4.14)
Таким образом точка А не лежит на заданных медианах, то есть в треугольнике АВС нам заданны уравнения медиан ВК и СМ. сделаем схематический чертёж. (Рис. 4.14)














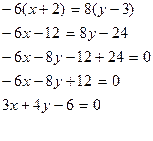

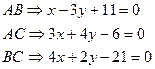

 , который перпендикулярен стороне АС.
, который перпендикулярен стороне АС.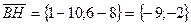

 , перпендикулярной стороне ВС.
, перпендикулярной стороне ВС.