
|
|
Приведение общего уравнения кривой к каноническому виду.Будем использовать два преобразования системы координат – параллельный перенос начала координат и поворот системы координат. Рассмотрим параллельный перенос начала координат. Если заданы две системы координат X, 0, Y и X1, 01, Y1 (рис. 9.4)
Рис. 9.4.
Формулы, связывающие координаты точки М в старой и новой системе координат будут: х1=х-х0 х=х1+х0 или у1=у-у0 у=у1+у0 где х0, у0 – координаты нового начала системы координат. Теперь рассмотрим преобразование поворота системы координат X, 0, Y и X1, 0, Y1, при чём система X1 0 Y1 повёрнута относительно исходной системы координат на угол a (рис. 9.5).
M
a 0
Рис. 9.5. a- угол поворота системы координат.
Выпишем формулы связывающие координаты точки М в системе координат X, 0, Y с координатами точки М в системе координат X1, 0, Y1
Рассмотрим теперь общее уравнение кривой второго порядка. Ах2+2Вху+Су2+2Dx+2Ey+F=0 Осуществляя поворот системы координат на угол a. Причём угол a выбирается таким образом, чтобы коэффициент при слагаемом, содержащим произведение ху стал равен нулю. Обозначим новую систему координат X1 0 Y1. В новой системе координат общее уравнение кривой будет: А1х12+С1у12+2D1x+2E1y+F=0 Нетрудно заметить, что коэффициент F не изменился. Если в полученном уравнении коэффициенты А1 и С1 одного знака т.е. если А1С1>0, то мы получаем кривую эллиптического типа. Если коэффициенты А1 и С1 разных знаков то есть А1С1<0,то уравнение определяет кривую гиперболического типа. Если один из коэффициентов А1 или С1 равен нулю, то А1С1=0, то получаем кривую параболического вида. Далее используя формулу параллельного переноса переходим из системы координат X1, 0, Y1 в систему координат X2, 02, Y2 в которой получаем канонические уравнения эллипса, гиперболы или параболы.
Пример 1: Найти эксцентриситет и дирректрисы эллипса заданного уравнением: х2+2у2=2 Решение:
Приведём уравнение эллипса к каноническому виду: Из этого уравнения видно, что а2=2; b2=1; тогда с2=а2-b2=2-1=1
Уравнения дирректрис
или х=-2;
таким образом уравнения дирректрис х=2 и х=-2.
Пример 2: Эллипс касается оси ординат в начале координат, а центр его находится в точке (5;0) составить уравнение эллипса, если известно, что его эксцентриситет равен 0,6.
Решение: Для нахождения основного уравнения эллипса используем каноническое уравнение эллипса со смещённым центром.
таким образом, одна из осей эллипса лежит на оси ОХ, так как эллипс касается оси ОУ в начале координат. Рассмотрим два случая. 1случай: Большая ось эллипса лежит на оси ОХ Тогда а=5;
для эллипса известно что: b2=a2-c2=25-9=16 тогда искомое уравнение эллипса имеет вид:
2 случай: Малая ось эллипса совпадает с осью ОХ.
Из соотношения
Тогда основное уравнение эллипса имеет вид:
Пример 3: Найти уравнение эллипса расстояние между фокусами которого равно 2, а расстояние между дирректрисами равно 10.
Решение: Воспользуемся каноническим уравнением эллипса с центром в начале координат.
По условию задачи 2с=2 следовательно с=1; Так расстояние между дирректриссами равно 10, а уравнения директрисс имеют вид:
тогда
Следовательно, имеем:
получаем искомое уравнение эллипса: Пример 4: Найти длины осей, координаты фокусов и эксцентриситет гиперболы заданной уравнением.
Решение: Преобразуем заданное уравнение к каноническому виду. Для этого разделим правую и левую часть на 144.
Из канонического уравнения можем записать длины полуосей гиперболы, причём фокальной осью является ось ОY. a=4; b=3 Находим длины действительной и мнимой оси гиперболы. Действительная ось гиперболы равна 2b=5. Мнимая ось гиперболы равна 2а=8. Для нахождения координат фокусов найдём значение (с) из формулы: b2=c2-a2 c2=a2+b2=16+9=25 c=5 тогда координаты фокусов будут: F1(0;5) и F2(0;-5). Значение эксцентриситета найдём из соотношения
Пример 5: Найти уравнение гиперболы если известно, что асимптоты даны уравнением Решение Сделаем схематический чертёж (рис 9.6)
0 5 10
-3
-6
Рис 9.6
Из уравнения асимптот (*) легко находить полуоси гиперболы а=5; b=3. Теперь остается выяснить какая из осей координат является фокальной. Для этого подставим координату точки М х=10 в уравнение асимптоты
Пример 6: Составить уравнение параболы, зная, что вершина её лежит вначале координат, направление оси симметрии совпадает с отрицательным направлением оси ОХ, а параметр р равен расстоянию от фокусов гиперболы 4х2-9у2-36=0 до асимптот. Решение: Будем искать уравнение параболы в виде у2=-2рх. Для нахождения параметра р приведём уравнение гиперболы к каноническому виду 4х2-9у2=36
из уравнения определяем полуоси гиперболы: а=3; b=2 найдём тогда координаты фокусов гиперболы уравнения асимптот гиперболы: возьмем фокус преобразуем уравнение асимптоты к виду 3у-2х=0 Используя формулу расстояния от точки до прямой на плоскости:
Получим:
таким образом параметр р=d=2 тогда уравнение искомой параболы: Пример 7: Дана парабола у2=6х, через точку (4,1) провести такую хорду, которая делилась бы в этой точке пополам. Решение: Сделаем вспомогательный чертеж (рис 9.7)
N
Рис. 9.7 Обозначим точки пересечения хорды и параболы К и N. Пусть координаты этих точек неизвестны К(хк;ук); N(хn;yn). Так как точки К и N лежат на известной параболе то имеем два состояния.
так как точка М делит отрезок КN пополам то имеем ещё 2 соотношения.
Рассмотрим систему.
решая квадратное уравнение находим:
По двум известным точкам М и N можно записать уравнение прямой: 1 случай: М(4;1)
2 случай: М(4;1)
В обоих случаях получили одно и то же уравнение хорды:3х-у-11=0
Пример 8: Построить кривую, определяемую уравнением Решение: Используя формулы поворота системы координат, перейдём в новую систему координат X1, 0, Y1
Приравняем к нулю коэффициент при члене х1* х2
тогда Прежде чем подставлять значения тригонометрических функций, преобразуем уравнение:
теперь подставим значения sina и cosa
полученное уравнение является уравнением параболического типа. Для получения канонического уравнения параболы необходимо осуществить параллельный перенос начала координат. Воспользуемся формулами параллельного переноса системы координат:
Получим
Для того чтобы получить каноническое уравнение параболы приравняем к нулю коэффициент при х2
Таким образом координаты начала координат новой системы X2, 02, Y2 в системе координат X1, 0, Y1 будут
Построим полученную параболу (рис 9.8)
02 х1
Рис 9.8. Задачи для самостоятельного решения
1. Определить координаты центра и радиус окружности, выраженной уравнением: х2+у2-4х+2у+1=0. 2. Найти уравнение окружности центр которой лежит в точке (4,7) и которая касается прямой 3х-4у+1=0. 3. Эллипс касается оси абсцисс в точке (8;0) и оси ординат в точке (5;0) составить уравнение эллипса, если известно что оси его параллельны осям координат. 4. Написать уравнение эллипса, малая полуось которого равна 5. Найти касательные к эллипсу 6. Найти длины осей, координаты фокусов и эксцентриситет гиперболы заданной уравнением: 25х2-144у2=3600. 7. Дан эллипс: 8. Найти касательные к гиперболе 9. Гипербола касается прямой х-у-3=0 в точке (5;2). Составить уравнение этой гиперболы. 10. Составить уравнение параболы, зная, что вершина её лежит в точке (-2;1), направление оси симметрии совпадает с отрицательным направлением оси ОY, а параметр Р равен расстоянию между дирректрисами эллипса 3х2+4у2-48=0. 11. Дана парабола у2=-8х. Через точку (-1;1) провести хорду, которая в этой точке делится пополам. 12. Найти уравнение касательной к параболе у2=16х, которая была бы параллельна прямой 2х-у+5=0. 13. Привести к каноническому виду уравнение кривой второго порядка. Построить график х2-ху+у2+2х-4у=0. 14. Найти центр кривой второго порядка, выражаемой уравнением 3х2-7ху+5у2+х-3у-3=0. 15. Составить каноническое, уравнения, а точнее построить кривые выраженные уравнениями: а)2ху-4-2у+3=0; б) х2-2у2-4х+2у+1=0; в) 5х2+12ху-22х-12у-19=0; г) х2+2ху+у2+3х+у=0; д) 6ху+8у2-12х-26у+11=0; е) х2-2ху+у2-10х-6у+25=0; ж) 7х2-24ху-38х+24у+175=0; з) 5х2+6ху+5у2-16х-16у-16=0; и) х2-2ху+у2-х-2у+3=0; к) 5х2+8ху+5у2-18х-18у+9=0.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 yy1
yy1 M
M 01
01 y0xo x1
y0xo x1
 x
x 
 y1 y
y1 y
 x1
x1
 x
x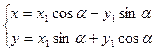

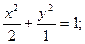
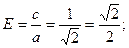
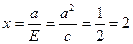
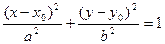 координаты центра эллипса нам заданы х0=5; у0=0;
координаты центра эллипса нам заданы х0=5; у0=0;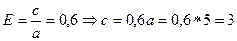
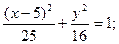
 Тогда b=5;
Тогда b=5;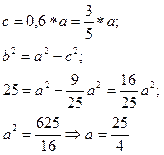
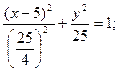
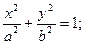
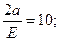
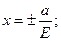
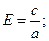
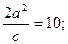 или а2=5.с=5.1=5; далее используя соотношение b2=a2-c2=5-1=4;
или а2=5.с=5.1=5; далее используя соотношение b2=a2-c2=5-1=4;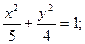
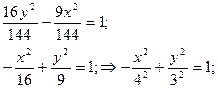
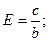 так как фокальной является ось ОY.
так как фокальной является ось ОY.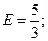
 и гипербола проходит через точку
и гипербола проходит через точку 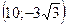
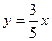 y
y
 3
3
 х
х
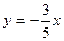

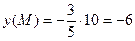 точка с координатами
точка с координатами 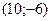 находится ниже точки
находится ниже точки 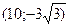 следовательно фокальной осью является ось ОХ и искомое уравнение гиперболы имеет вид:
следовательно фокальной осью является ось ОХ и искомое уравнение гиперболы имеет вид: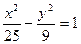
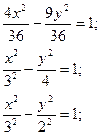
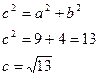
 и
и 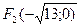
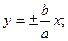
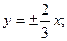
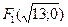 и асимптоту
и асимптоту 
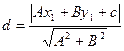
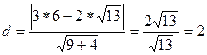
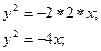
 y
y 


 x
x  0
0 K
K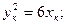



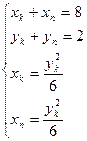
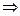
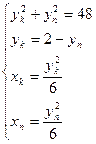
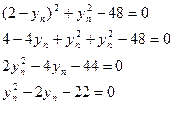
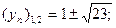
 соответственно:
соответственно: 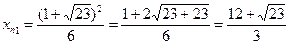
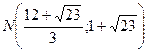 ;
;


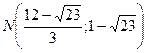

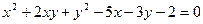 ;
;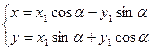
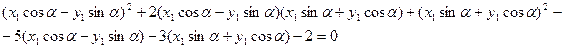
 Сгруппируем слагаемые
Сгруппируем слагаемые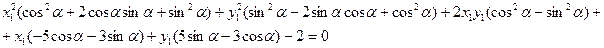
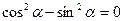
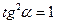


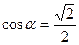

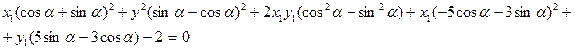
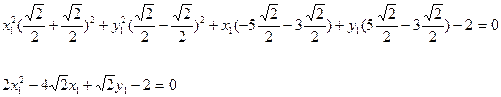
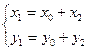
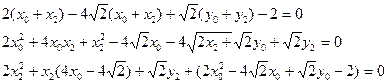
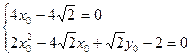
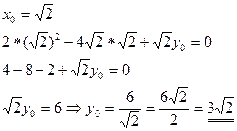
 Каноническое уравнение параболы в системе координат X2, 02, Y2 имеет вид:
Каноническое уравнение параболы в системе координат X2, 02, Y2 имеет вид: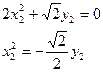
 у2 у х2
у2 у х2
 у1
у1
 0 х
0 х  и дирректисами которого служат прямые
и дирректисами которого служат прямые 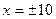 .
.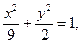 проходящие через точку (-3;1).
проходящие через точку (-3;1).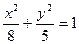 . Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы в вершинах данного эллипса.
. Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы в вершинах данного эллипса.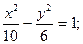 в точках пересечения её с прямой 3х-5у=0.
в точках пересечения её с прямой 3х-5у=0.