
|
|
Решение систем линейных уравнений матричным способом.Этот метод, как и предыдущий, используется для решения квадратичных систем, то есть систем имеющих одинаковое число уравнений и неизвестных. Причём для применения этого метода основная матрица системы должна быть невырожденной, и таким образом для нее существует обратная матрица. Рассмотрим применение этого метода на примере системы трёх уравнений с тремя неизвестными.
Для данной системы уравнений имеем основную матрицу системы, матрицу столбец свободных членов и матрицу столбец неизвестных:
тогда система уравнений в матричном виде имеет вид:
так как матрица А по условию является невырожденной то для неё существует обратная матрица А-1. Домножим матричное уравнение на матрицу А-1 слева, получим. Произведение Таким образом, для решения системы матричным методом, необходимо найти обратную матрицу основной матрицы системы А и затем, умножив ее на матрицу столбец получим матрицу столбец неизвестных. Рассмотрим примеры, связанные с темой главы 7.
Пример 1: Решить систему уравнений тремя методами: 1. Методом Гаусса; 2. По формулам Крамера; 3. Матричным методом.
Решение методом Гаусса: Для использования этого метода выпишем расширенную матрицу системы, включив в нее столбец контрольных сумм КΣ и столбец в котором указываем базисные переменные:
В конечной матрице содержатся только базисные неизвестные, поэтому система имеет единственное решение. х1=-1; х2=2; х3=0. Приведём описание действий, которые были выполнены в процессе элементарных преобразований. 1. В качестве разрешающего элемента выбран элемент, стоящий в первой строке и первом столбце. С помощью элементарных преобразований в первом столбце получены нулевые элементы во второй и третьей строках. В результате этих преобразований переменная х1 стала базисной. 2. Элементы второй строки умножаем на 3. В качестве разрешающего элемента выберем элемент второй строки расположенный во втором столбце. С помощью элементарных преобразований во втором столбце получаем нулевые элементы в первой и третьей строках. В результате этих преобразований переменная х2 становится базисной. 4. Элементы третьей строки умножаем на 5. В качестве разрешающего элемента выбираем элемент третьей строки стоящий в третьем столбце. С помощью элементарных преобразований в третьем столбце получены нулевые элементы в первой и второй строках.
Решение системы по формулам Крамера: Для использования формул Крамера, необходимо выписать четыре определителя третьего порядка.
тогда используя формулы Крамера находим х1, х2, х3:
Решение системы матричным методом: Для решения системы матричным методом выпишем основную матрицу системы, матрицу столбец неизвестных и матрицу столбец свободных членов.
Для использования матричного метода необходимо найти обратную матрицы А-1. Вычислим сначала определитель основной матрицы.
Матрица невырожденная, следовательно, существует обратная матрица. Найдём алгебраические дополнения ко всем элементам определителя основной матрицы:
тогда обратная матрица имеет вид:
найдём матрицу Х.
таким образом х1=-1; х2=2; х3=0. Задачи для самостоятельного решения 1. Решить систему по формулам Крамера и матричным способом.
2. Решить систему уравнений методом Жордана Гаусса. a. b. c. d.
Глава 8 Арифметическое n-мерное векторное пространство. Арифметические векторы. Выше мы дали понятие вектора на плоскости и в пространстве. На плоскости вектор определяется двумя координатами, то есть парой чисел. В пространстве вектор определяется уже тройкой чисел. Причём в этих случаях возможна была геометрическая интерпретация. Во многих задачах экономики приходится встречаться с величинами, которые определяются гораздо большим числом характеристик чем три. Поэтому обобщим понятие вектора на тот случай, когда число характеристик равно n. Определение 1: Арифметическим n - мерным вектором называется любая последовательность из n действительных чисел: а1, а2,…,аn Обозначать арифметический вектор будем как и обычный вектор чертой сверху, числа а1, а2, …, аn называются компонентами или координатами вектора.
Пример:
Имеем арифметический вектор с координатами –1, 2, 3, 0, 1. Многие определения, введённые для векторов, на плоскости и в пространстве фактически обозначаются на случай двух координат. Тем не менее, повторим их. Определение 2: Дав вектора
называются равными если: а1=b1; а2=b2…an=bn. равенство векторов записывают: Определение 3: Вектор, у которого все компоненты равны нулю, называется нулевым вектором (0,0,…0). Обозначается: Определение 4: Суммой двух векторов Определение 5: Произведением вектора
Операции сложения двух арифметических векторов и умножение арифметического вектора на число обладает следующими свойствами. 1. 2. 3. 4. Для любого вектора 5. 6. 7. 8. Приведённые свойства почти очевидны и являются следствиями свойств сложения и умножения чисел. Определение 6: Арифметическим n – мерным пространством называется множество всех n – мерных арифметических векторов с введёнными выше операциями сложения векторов и умножения вектора на число. Обозначается Rn. Очень важным понятием для арифметических векторов является скалярное произведение, но для арифметических векторов оно определяется несколько иначе. Определение 7: Скалярным произведением двух векторов Скалярное произведение обладает теми же свойствами, которые были введены для трёхмерных векторов. Модуль арифметического n – мерного вектора определяется, так же как и в трёхмерном пространстве.
Аналогично вводится и понятие угла между двумя не нулевыми векторами.
Определение 8: Неравенство Коши-Буияковского. Для любых двух векторов Определение 9: Два арифметических вектора

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ;
;  ;
;  ;
;

 , так как ЕХ=Х окончательно получим Х=А-1В.
, так как ЕХ=Х окончательно получим Х=А-1В.

 .
.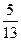 .
.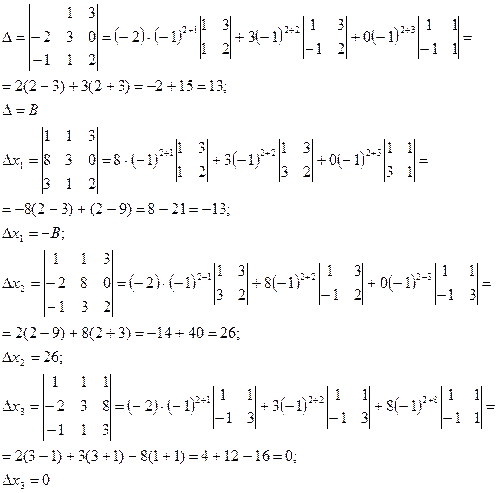
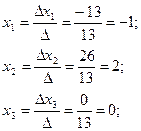

 ;
;  (Смотри предыдущий пример)
(Смотри предыдущий пример)







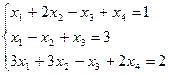


 и
и  с одинаковым числом координат:
с одинаковым числом координат:
 .
.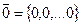 .
.
 называется вектор.
называется вектор.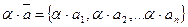
 - коммутативность сложения.
- коммутативность сложения. - ассоциативность сложения.
- ассоциативность сложения. - для любого
- для любого  - дистрибутивность относительно суммы векторов.
- дистрибутивность относительно суммы векторов. - дистрибутивность относительно суммы чисел.
- дистрибутивность относительно суммы чисел. - ассоциативность относительно умножения на число.
- ассоциативность относительно умножения на число. - существование нейтрального элемента при умножении.
- существование нейтрального элемента при умножении.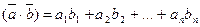 .
.


 или
или  .
.