
|
|
Параметрические уравнения прямой.
Приравнивая в канонических уравнениях прямой каждую из дробей некоторому параметру t:
Получим уравнения выражающие текущие координаты каждой точки прямой через параметр t.
таким образом параметрические уравнения прямой имеют вид:
Уравнения прямой проходящей через две заданные точки. Пусть заданы две точки М1 (x1,y1,z1) и М2 (x2,y2,z2). Уравнения прямой, проходящей через две заданные точки получаются так же, как аналогичное такое уравнение на плоскости. Поэтому сразу приведём вид этого уравнения.
Прямая на пересечении двух плоскостей. Общее уравнение прямой в пространстве.
Если рассмотреть две не параллельные плоскости, то их пересечением будет прямая.
Если нормальные вектора Ниже при рассмотрении примеров мы покажем способ преобразования таких уравнений прямой к каноническим уравнениям.
5.4 Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых.
Углом между двумя прямыми в пространстве будем называть любой из углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным. Пусть две прямые заданны своими каноническими уравнениями.
За угол между двумя прямыми примем угол между направляющими векторами.
Условие перпендикулярности двух прямых сводится к условию перпендикулярности их направляющих векторов Условие параллельности двух прямых сводится к условию параллельности их направляющих векторов
5.5 Взаимное расположение прямой и плоскости. Пусть заданы уравнения прямой:
Рис 5.5 В случае перпендикулярности прямой к плоскости направляющий вектор прямой и нормальный вектор к плоскости коллинеарны. Таким образом, условие перпендикулярности прямой и плоскости сводится к условию коллинеарности векторов
В случае параллельности прямой и плоскости их указанные выше вектора взаимно перпендикулярны. Поэтому условие параллельности прямой и плоскости сводится к условию перпендикулярности векторов Ниже рассмотрены примеры решения задач, связанных с темой главы 5. Пример 1: Составить уравнение плоскости, проходящей через точку А (1,2,4) перпендикулярную прямой, заданной уравнением:
Решение: Воспользуемся уравнением плоскости проходящей через заданную точку перпендикулярную заданному вектору. А(х-х0)+В(у-у0)+С(z-z0)=0 В качестве точки возьмём точку А (1,2,4), через которую проходит по условию плоскость. Зная канонические уравнения прямой, мы знаем вектор, параллельный прямой В силу того, что по условию прямая перпендикулярна искомой плоскости, направляющий вектор может быть взят в качестве нормального вектора плоскости. Таким образом уравнение плоскости получим в виде: 2(х-1)+1(у-2)+4(z-4)=0 2х+у+4z-16=0 2х+у+4z-20=0 Пример 2: Найти на плоскости 4х-7у+5z-20=0 такую точку Р, для которой ОР составляет с осями координат одинаковые углы. Решение:
z
х Рис 5.6
Пуст точка Р имеет координаты
Найдём проекции вектора
тогда легко находятся направляющие косинусы этого вектора.
Из равенства направляющих косинусов следует равенство: хр=ур=zр так как точка Р лежит на плоскости, то подстановка координат этой точки в уравнение плоскости обращает его в тождество. 4хр-7хр+5хр-20=0 2хр=20 хр=10 Соответственно: ур=10; zр=10. Таким образом искомая точка Р имеет координаты Р(10;10;10)
Пример 3: Даны две точки А (2,-1,-2) и В (8,-7,5). Найти уравнение плоскости, проходящей через точку В, перпендикулярную отрезку АВ. Решение: Для решения задачи воспользуемся уравнением плоскости, проходящей через заданную точку перпендикулярную заданному вектору. А(х-х0)+В(у-у0)+C(z-z0)=0 В качестве точки используем точку В (8,-7,5), а в качестве вектора, перпендикулярного плоскости вектор
тогда уравнение плоскости получим в виде: 6(х-8)-6(у+7)+7(z-5)=0 6х-48-6у-42+7z-35=0 6х-6у+7z-35=0 6х-6у+7z-125=0 Пример 4: Найти уравнение плоскости, параллельной оси ОY и проходящей через точки К(1,-5,1) и М(3,2,-2). Решение: Так как плоскость параллельна оси ОY, то воспользуемся неполным уравнением плоскости. Ax+Cz+D=0 В силу того, что точки К и М лежат на плоскости , получим два условия.
Выразим из этих условий коэффициенты А и С через D.
Подставим найденные коэффициенты в неполное уравнение плоскости:
так как
Пример 5: Найти уравнение плоскости проходящей через три точки М(7,6,7), К(5,10,5), R(-1,8,9) Решение: Воспользуемся уравнением плоскости проходящей через 3 заданные точки.
подставляя координаты точек М,К,R как первой, второй и третьей получим:
раскроем определитель по 1ой строке.
Пример 6: Найти уравнение плоскости, проходящей через точки М1 (8,-3,1); М2 (4,7,2) и перпендикулярно плоскости 3х+5у-7z-21=0 Решение: Сделаем схематический чертёж (Рис 5.7)
Рис 5.7
Обозначим заданную плоскость Р2 а искомую плоскость Р2.. Из уравнения заданной плоскости Р1 определяем проекции вектора
Вектор Найдём проекции вектора
теперь мы имеем два вектора
Векторы
Далее, используем уравнение плоскости, проходящей через заданную точку перпендикулярную вектору. В качестве точки можно взять любую из точек М1 или М2, например М1(8,-3,1); В качестве нормального вектора к плоскости Р2 берём 74(х-8)+25(у+3)+50(z-1)=0 3(х-8)+(у-3)+2(z-1)=0 3х-24+у+3+27-2=0 3х+у+2z-23=0
Пример 7: Прямая задана пересечением двух плоскостей. Найти канонические уравнения прямой.
Решение: Имеем уравнение в виде:
Надо найти точку (х0,у0,z0), через которую проходит прямая и направляющий вектор Выберем произвольно одну из координат. Например, z=1, тогда получим систему двух уравнений с двумя неизвестными:
Таким образом, мы нашли точку лежащую на искомой прямой (2,0,1). В качестве направляющего вектора
Таким образом, направляющий вектор прямой имеет проекции
Итак искомое каноническое уравнение имеет вид:
Пример 8: Найти координаты точки пересечения прямой Решение: Запишем заданное уравнение прямой в параметрическом виде. х=3t-2; y=-t+2; z=2t-1 каждой точке прямой соответствует единственное значение параметра t. Для нахождения параметра t соответствующего точке пересечения прямой и плоскости подставим в уравнение плоскости выражение х, у, z через параметр t. 2(3t-2)+(-t+2)+3(2t-1)-8=0 6t-4-3t+6+6t-3-8=0 9t-9=0 t=1 тогда координаты искомой точки
искомая точка пересечения имеет координаты (1;1;1).
Пример 9: Найти уравнение плоскости проходящей через параллельные прямые.
Решение: Сделаем схематический чертёж (Рис 5.9)
Рис 5.9
Из заданных уравнений прямых
Таким образом, имеем два неколлинеарных вектора
Пример 10: Найти расстояние между двумя заданными параллельными прямыми.
Решение: Сделаем схематический чертёж (Рис 5.10)
p M
M2 L2
Для решения этой задачи найдём уравнение вспомогательной плоскости Р перпендикулярной параллельным прямым L1 и L2 и проходящей через точку М1 (1,-1,2) лежащую на прямой L1. В качестве направляющего вектора этой плоскости может быть взять направляющий вектор прямой L1 1(х-1)-2(у+1)+3(z-2)=0 х-1-2у-2+3z-6=0 х-2у+3z-9=0 Найдём точку пересечения прямой L2 и плоскости Р, для этого уравнение прямой L2 представим в параметрическом виде: x=t; y=-2t+1; z=3t-2 Находим значение параметра t соответствующее точке пересечения прямой L2 и плоскости Р, точка М2
таким образом координаты точки М2
Найдём расстояние между двумя точками М1 и М2 это и будет расстояние между параллельными прямыми L1 и L2.
Задачи для самостоятельного решения 1. Проверить проходит ли плоскость 3х-5у+2z-17=0 через точки А(4,1,2); В(2,-1,3); С(7,1,2) 2. Найти на плоскости, заданной уравнением у+z-2=0, такую точку Р, чтобы прямая ОР составляла с осями ОY и oz углы 600. 3. Даны две точки А(-7,2,-1) и В(3,4,10). Найти уравнение плоскости проходящей через точку В перпендикулярную и отрезку АВ. 4. Найти уравнение плоскости проходящей через ось ОХ и через точку (3,2,-7). 5. Найти угол между плоскостями х+у-11=0 и 3х+8=0. 6. Найти уравнение плоскости проходящей через начало координат и перпендикулярной плоскостям: х-у+z-7=0; 3х+2у-11z+5=0. 7. Определить расстояние от точки А(1,2,1) до плоскости х+2у+2z-10=0. 8. Найти расстояние между параллельными плоскостями: 3х+2у-6z-56=0; 3х+2у-6z-35=0. 9. Определить лежат ли точки А(5,-2,-3) и В(8,3,1) на прямой заданной пересечением двух плоскостей:
10. Привести уравнение прямой, заданной пересечением двух плоскостей к каноническому виду:
11. Проверить лежат ли прямые в одной плоскости.
12. Найти угол между прямой и плоскостью, если прямая задана как пересечение двух плоскостей: 13. Найти уравнение плоскости проходящей через точку (-1,-2,-3) и параллельно прямым
14. Составить уравнение плоскости проходящей через прямую, заданную пересечением двух плоскостей: 15. Решить задачу, рассмотренную в примере 11 без составления уравнения вспомогательной плоскости.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|





 и
и  неколенеарны.
неколенеарны.
 и
и 
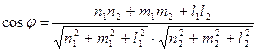
 и
и  , то есть к равенству нулю скалярного произведения:
, то есть к равенству нулю скалярного произведения:  или в координатной форме:
или в координатной форме:  .
.

 и плоскости
и плоскости  . Углом
. Углом  между прямой и плоскостью будем называть любой из двух смежных углов, образованных прямой и ее проекцией на плоскость (Рис 5.5).
между прямой и плоскостью будем называть любой из двух смежных углов, образованных прямой и ее проекцией на плоскость (Рис 5.5).






 или в координатной форме:
или в координатной форме:  .
.
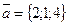 .
. Сделаем схематический чертёж. (Рис. 5.6)
Сделаем схематический чертёж. (Рис. 5.6)
 Р
Р

 у
у . Так как вектор
. Так как вектор  составляет одинаковые углы с осями координат, то направляющие косинусы этого вектора равны между собой
составляет одинаковые углы с осями координат, то направляющие косинусы этого вектора равны между собой




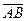 . Найдём проекции вектора
. Найдём проекции вектора 



 , то сокращаем D:
, то сокращаем D:

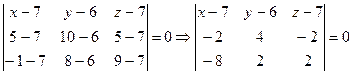


 , перпендикулярного плоскости Р1.
, перпендикулярного плоскости Р1.
 лежащего в плоскости Р2:
лежащего в плоскости Р2:
 , равный векторному произведению векторов
, равный векторному произведению векторов  и
и  будет перпендикулярен плоскости Р2, т. к. он перпендикулярен
будет перпендикулярен плоскости Р2, т. к. он перпендикулярен 
 .
.

 Рис 5.8
Рис 5.8
 .
.
 искомой прямой возьмём векторное произведения
искомой прямой возьмём векторное произведения 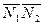 векторов
векторов  , а значит параллельно искомой прямой.
, а значит параллельно искомой прямой.

 . Используя уравнение прямой проходящий через заданную точку параллельно заданному вектору:
. Используя уравнение прямой проходящий через заданную точку параллельно заданному вектору:

 и плоскости 2x+3y+3z-8=0
и плоскости 2x+3y+3z-8=0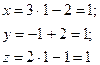



 и
и  определяем проекции направляющих векторов этих прямых
определяем проекции направляющих векторов этих прямых 
 . Найдём проекции вектора
. Найдём проекции вектора  , лежащего в плоскости Р, а точки
, лежащего в плоскости Р, а точки  и
и  берём из канонических уравнений прямых М1 (1,-1,2) и М2 (0,1,-2).
берём из канонических уравнений прямых М1 (1,-1,2) и М2 (0,1,-2).
 и
и  Теперь у нас есть вектор
Теперь у нас есть вектор  лежащая в плоскости. Тогда искомое уравнение плоскости имеет вид:
лежащая в плоскости. Тогда искомое уравнение плоскости имеет вид: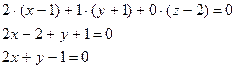




 1 S1 L1
1 S1 L1
 . Тогда уравнение плоскости Р
. Тогда уравнение плоскости Р

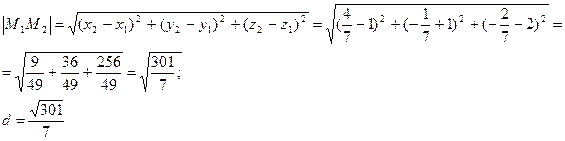



 , а уравнение плоскости имеет вид: 6х+15у-10z+31=0.
, а уравнение плоскости имеет вид: 6х+15у-10z+31=0.
 и параллельно прямой х=у=z.
и параллельно прямой х=у=z.