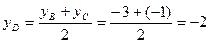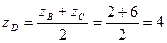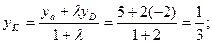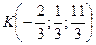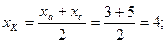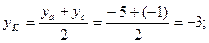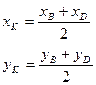|
|
Глава 4 Прямая на плоскости.УКД 51.658.01 Руководство к решению задач по аналитической геометрии и векторной алгебре. Учебное пособие. /И.И. Антонова, О.М. Кокшаров – М.:МГУПИ, 2006. – 114 стр.
Настоящее пособие предназначено для подготовки студентов различных форм обучения по специальностям: 230101 и 010502. Работа рассмотрена и одобрена на заседании кафедры ИТ-1 «Высшей математики».
© Антонова И.И., Кокшаров О.М., 2006 © МГУПИ, 2006 Содержание:
Глава 1 Система координат. Операции над векторами.............................. 4 Глава 2 Определители................................................................................... 12 Глава 3 Понятие скалярного, векторного и смешанного произведения векторов............................................................................................................. 18 Глава 4 Прямая на плоскости....................................................................... 30 Глава 5 Уравнение плоскости. Уравнение прямой в пространстве....... 48 Глава 6 Матрицы и их свойства................................................................... 66 Глава 7 Системы линейных уравнений...................................................... 73 Глава 8 Арифметическое n-терное векторное пространство. Преобразование декартовых координат на плоскости........................................... 82 Глава 9 Поверхности второго порядка. Преобразование декартовых координат на плоскости.......................................................................................... 89 Глава 10 Поверхности второго порядка.................................................. 104 Приложение.................................................................................................. 112
Глава1 Система координат. Операции над векторами. 1.1 Понятие о системах координат. В курсе средней школы вы уже знакомились с различными системами координат. Напомним о них. Рассмотрим самую простую систему координат на прямой.
М(х)
0 1 х Рис. 1.1
Если установлено положительное направление, на прямой зафиксирована определённая точка, которую будем называть началом координат, установлена единица масштаба, то говорят, что на прямой задана система координат. Если на прямой задана система координат, то положение каждой точки на прямой можно определить одним числом. Аналогично вводится понятие системы координат на плоскости, которая используется уже для определения положения точек на плоскости.
0 М1 х
Рис. 1.2 Если на плоскости зафиксирована точка 0 (начало координат), через точку 0 проведены две взаимно-перпендикулярные оси ОХ и ОУ (Рис. 1.2), на осях установлены единицы масштаба, то говорят, что на плоскости задана прямоугольная система координат. Если на плоскости задана прямоугольная система координат, то любая точка плоскости задаётся упорядоченной парой чисел, которые называются координатами. Если рассмотреть в пространстве фиксированную точку (начало координат), провести через неё три взаимно-перпендикулярные прямые оси ОХ,ОУ,ОZ, (Рис. 1.3) на осях установить единицы масштаба, то говорят, что в пространстве задана прямоугольная система координат.
М1 Р(х,у)
х Рис. 1.3 В пространстве каждой точке соответствуем единственная упорядоченная тройка чисел. Справедливо и обратное утверждение.
1.2 Понятие вектора. Действия над векторами.
Введём теперь в рассмотрение понятие векторной величины.
· Скалярная величина – это такая величина, которая определяется только числовым значением. (масса, плотность, объем, и т.д.). В математике определение вектора даётся абстрактно. · Вектором называют отрезок прямой на котором установлено направление.
Обозначения:
Рис. 1.4 Расстояние между началом и концом вектора называют длиной вектора (модулем) обозначают · Если начало и конец вектора совпадают то вектор называется нулевым. · Векторы · Два вектора o Их длины равны, т.е. o Они коллинеарные o Одинаково направлены · Векторы o Их длины равны o Они коллинеарные o Они противоположно направленные · Суммой двух векторов
Рис. 1.5 Операция сложения векторов обладает свойством переместительности и сочетательности 1) 2) Операция вычитания векторов вводится как операция, обратная сложению. ·
проведён из конца вектора в конец вектора
Рис. 1.6 · произведением вектора 1. 2. Вектор Свойства умножения вектора на число: а) б) в) Используя операцию умножения вектора на число можно ввести аналитическое условие коллинеарности двух векторов. · Чтобы вектора
где Прежде чем перейти к исследованию связи векторов и систем координат необходимо ввести ещё одну операцию действия над векторами, это проекция вектора на ось.
· Числовой проекцией вектора
Рис. 1.7 Таким образом: Прl Прl Свойства операций: 1. Проекция суммы векторов равна сумме проекций слагаемых векторов на ту же ось. Прl 2. Проекция вектора 3. Постоянный множитель можно выносить за знак проекции Пре
Мы рассмотрели способ задания вектора с помощью определения его длины и направления. Однако большой интерес представляет способ задания вектора с помощью чисел. Пусть в пространстве задана прямоугольная система координат ОХУZ. Рассмотрим в пространстве произвольный вектор x=Прох y=Проу z=Проz x, y, z – координаты вектора.
М1
х Рис. 1.8
Так как проекция вектора на ось определяется однозначно, то каждому вектору Рассмотрим операции над векторами, заданными своими координатами. 1. При сложении векторов их координаты складываются. Так если
2. При вычитании векторов их координаты вычитаются.
3. При умножении вектора на число его координаты умножаются на это число. Пусть 4. Если заданы координаты начала и конца вектора
5. Если два вектора
то для того чтобы они были коллинеарны необходимо и достаточно, чтобы их координаты были попорциональны.
6. Если заданы координаты концов отрезка
то координаты точки
в случае деления отрезка напополам
7. Если вектор
8. Если вектор
М1
х Рис. 1.9 то косинусы этих углов, называемые направляющими косинусами определяются следующими соотношениями.
9. Если в пространстве задана прямоугольная система координат ОХУZ, и в направлении осей координат заданы единичные векторы
М1
х
Рис. 1.10
Примеры решения задач. Задача 1: Найти координаты центра тяжести треугольника с вершинами: А (-4;5;3), В(0;-3;2), С(2;-1;6) Решение: В
C Рис. 1.11 Известно, что центр тяжести треугольника расположен в точке К пересечения медиан (Рис. 1.11), причём
используя формулу деления отрезка в заданном отношении найдём координаты точки К.
таким образом точка К имеет координаты: Задача 2: Даны три последовательные вершины параллелограмма: А(3;5), В(1;1), С(5,-1). Найти координаты четвёртой вершины? Решение:
К
А D Рис. 1.12 Известно из свойств параллелограмма, что диагонали в точке пересечения делятся пополам (Рис. 1.12). Тогда легко найти координаты точки К, как середины диагонали АС.
К(4;-3) используя то, что точка К является серединой диагонали ВD можем записать соотношения:
Подставляя координаты точек В и К получим:
таким образом, точка D имеет координаты: D(7;-7)
Глава1 Система координат. Операции над векторами. 1.1 Понятие о системах координат. В курсе средней школы вы уже знакомились с различными системами координат. Напомним о них. Рассмотрим самую простую систему координат на прямой.
М(х)
0 1 х Рис. 1.1
Если установлено положительное направление, на прямой зафиксирована определённая точка, которую будем называть началом координат, установлена единица масштаба, то говорят, что на прямой задана система координат. Если на прямой задана система координат, то положение каждой точки на прямой можно определить одним числом. Аналогично вводится понятие системы координат на плоскости, которая используется уже для определения положения точек на плоскости.
0 М1 х
Рис. 1.2 Если на плоскости зафиксирована точка 0 (начало координат), через точку 0 проведены две взаимно-перпендикулярные оси ОХ и ОУ (Рис. 1.2), на осях установлены единицы масштаба, то говорят, что на плоскости задана прямоугольная система координат. Если на плоскости задана прямоугольная система координат, то любая точка плоскости задаётся упорядоченной парой чисел, которые называются координатами. Если рассмотреть в пространстве фиксированную точку (начало координат), провести через неё три взаимно-перпендикулярные прямые оси ОХ,ОУ,ОZ, (Рис. 1.3) на осях установить единицы масштаба, то говорят, что в пространстве задана прямоугольная система координат.
М1 Р(х,у)
х Рис. 1.3 В пространстве каждой точке соответствуем единственная упорядоченная тройка чисел. Справедливо и обратное утверждение.
1.2 Понятие вектора. Действия над векторами.
Введём теперь в рассмотрение понятие векторной величины.
· Скалярная величина – это такая величина, которая определяется только числовым значением. (масса, плотность, объем, и т.д.). В математике определение вектора даётся абстрактно. · Вектором называют отрезок прямой на котором установлено направление.
Обозначения:
Рис. 1.4 Расстояние между началом и концом вектора называют длиной вектора (модулем) обозначают · Если начало и конец вектора совпадают то вектор называется нулевым. · Векторы · Два вектора o Их длины равны, т.е. o Они коллинеарные o Одинаково направлены · Векторы o Их длины равны o Они коллинеарные o Они противоположно направленные · Суммой двух векторов
Рис. 1.5 Операция сложения векторов обладает свойством переместительности и сочетательности 1) 2) Операция вычитания векторов вводится как операция, обратная сложению. ·
проведён из конца вектора в конец вектора
Рис. 1.6 · произведением вектора 1. 2. Вектор Свойства умножения вектора на число: а) б) в) Используя операцию умножения вектора на число можно ввести аналитическое условие коллинеарности двух векторов. · Чтобы вектора
где Прежде чем перейти к исследованию связи векторов и систем координат необходимо ввести ещё одну операцию действия над векторами, это проекция вектора на ось.
· Числовой проекцией вектора
Рис. 1.7 Таким образом: Прl Прl Свойства операций: 4. Проекция суммы векторов равна сумме проекций слагаемых векторов на ту же ось. Прl 5. Проекция вектора 6. Постоянный множитель можно выносить за знак проекции Пре
Мы рассмотрели способ задания вектора с помощью определения его длины и направления. Однако большой интерес представляет способ задания вектора с помощью чисел. Пусть в пространстве задана прямоугольная система координат ОХУZ. Рассмотрим в пространстве произвольный вектор x=Прох y=Проу z=Проz x, y, z – координаты вектора.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 у
у
 М2 М(х,у)
М2 М(х,у)
 z
z
 М3
М3
 М(х,у,z)
М(х,у,z)

 0 М2 у
0 М2 у А – начало вектора В
А – начало вектора В В – конец вектора
В – конец вектора
 А
А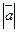 или
или 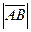 .
. называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
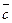 проведённый из начала вектора
проведённый из начала вектора 
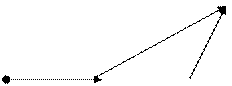
 (переместительные)
(переместительные)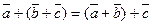 (сочетательные)
(сочетательные)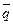 , что
, что
 Вектор
Вектор 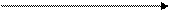
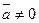 на число
на число 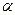 называется вектор
называется вектор 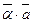
 и противоположен вектору
и противоположен вектору  .
.

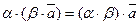

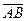 на ось
на ось 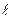 называется число равное длине вектора
называется число равное длине вектора 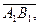 где
где 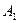 и
и  проекции на ось
проекции на ось 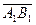 совпадает с направлением оси
совпадает с направлением оси 






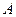

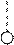


 , если направление
, если направление 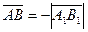 , если направление вектора
, если направление вектора 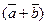 =Прl
=Прl  между осью
между осью 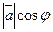 .
. =
=  z
z
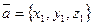 и
и 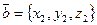 , то
, то 

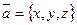 и
и 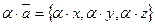
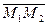 - точки
- точки  и
и 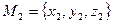 , то координаты вектора
, то координаты вектора 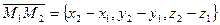
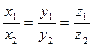
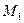 ;
; 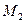 и некоторая точка М делит отрезок в заданном отношении
и некоторая точка М делит отрезок в заданном отношении  , то есть:
, то есть:


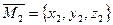
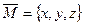 находятся по формулам:
находятся по формулам:
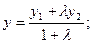
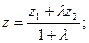
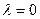 и формулы преобразуются к виду:
и формулы преобразуются к виду: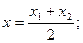

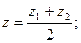

 (Рис. 1.9)
(Рис. 1.9)


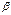


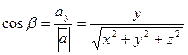

 (Рис. 1.10), то любой вектор
(Рис. 1.10), то любой вектор 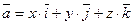
 z
z


 D
D K
K A
A найдём координаты точки D, как середины отрезка ВС
найдём координаты точки D, как середины отрезка ВС