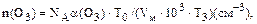|
|
Дисперсные системы в атмосфере
Дисперсные системы, состоящие из твердых или жидких частиц, распределенных в газовой фазе, называют аэрозолями. Для существования устойчивого аэрозоля необходимо выполнение следующих условий: 1) скорость седиментации частиц мала; 2) силами инерции при перемещении частиц можно пренебречь (отношение сил инерции к силам вязкости мало); 3) броуновское движение частиц весьма эффективно; 4) система характеризуется высокой удельной поверхностью. Физический смысл этих условий сводится к следующему. Обычно внешней силой, воздействующей на эрозольную частицу, является гравитация. Это означает, что время жизни частицы в атмосфере определяется скоростью ее седиментации. Если радиус частицы больше, чем величина среднего свободного пробега молекулы, то скорость седиментации Wg описывается уравнением Стокса: Wg = 2r2rчq/(9m), (130) где r и rч– радиус и плотность частицы (в сферическом приближении); q – ускорение свободного падения; m – динамическая вязкость газа (для воздуха при 298 К m = 1,81 . 10–4 Па . с). В атмосфере Wgзависит от высоты над уровнем моря. Более того, в тропосфере восходящие потоки еще больше затрудняют интерпретацию понятияWg. Все же в слое воздуха можно в качестве верхнего пределаWg принять значение 0,1 м . с–1 при rч = 1 г . см–3 (первый критерий устойчивости). Данное значение Wg определяет скорость падения частицы радиуса 30 мкм. Однако в атмосфере встречаются и большие по размеру частицы, которые благодаря восходящим атмосферным потокам могут быть обнаружены на значительных расстояниях от источника выброса. Второй критерий устойчивости формулируется как rWr/m = Re < 1, (131) где r – плотность воздуха; W – скорость движения частицы, обусловленного внешним воздействием; Rе – число Рейнольдса. Таким образом, в устойчивых аэрозольных системах при нормальных атмосферных условиях скорость движения частицы радиуса 10 мкм не может превысить 30 см . с–1, а если радиус равен 30 мкм, то критическая скорость равна 10 см . с–1. Если внешнее воздействие обусловлено силой гравитации, то второй критерий эквивалентен первому. Броуновское движение аэрозольных частиц является следствием их случайных соударений с молекулами газов, составляющих атмосферу. Скорость броуновского движения увеличивается с уменьшением размера частиц и обычно принимается во внимание, если r < 0,5 мкм (третий критерий устойчивости). Четвертый критерий удовлетворяется, если площадь поверхности частицы превосходит ее объем по крайней мере в 10 раз. Именно поэтому поверхностные явления играют значительную роль в физико-химических превращениях аэрозолей. Перечисленные критерии позволяют установить верхний предел размеров аэрозольных частиц. Что же касается нижнего предела, то в его оценке обычно исходят из следующих посылок. Система рассматривается как аэрозольная, если размер частиц больше, чем размер молекул газовой фазы, в которой частицы распределены. В то же время mч » тr, где mч и mг — массы аэрозольной частицы и молекулы газа соответственно. Исходя из среднего размера молекул основных компонентов атмосферы, можно принять значение 1 нм в качестве нижнего предела. Важным следствием броуновского движения является столкновение частиц и их последующая коагуляция. Скорость коагуляции описывается уравнением:
где N – число частиц в единице объема; t – время; D – коэффициент диффузии частиц; D = kT(1+AL/t)6pmr) (133) где k – константа Больцмана; Т – абсолютная температура; А – поправочный коэффициент Стокса – Кунихема; L – средняя длина свободного пробега молекул газа (L = 65,3 нм при нормальных условиях). Коэффициент А описывается уравнением: A = 1,257 + 0,400exp(–1,10r/L) (134) Из уравнений (132) и (133) получаем:
Из уравнения (135) следует, что скорость выведения частиц из атмосферы в результате их коагуляции пропорциональна квадрату концентрации и обратно пропорциональна радиусу частиц. Таким образом, выведение малых по размеру, но присутствующих в высоких концентрациях аэрозольных частиц – высокоэффективный процесс. Аэрозоли обычно подразделяют на две большие группы по происхождению и по размерам частиц – микро- и макрочастицы. Микрочастицы (радиус меньше 0,5-1,0 мкм) образуются в процессах коагуляции и конденсации, тогда как макрочастицы (радиус > 1,0 мкм) возникают в основном при дезинтеграции поверхности Земли. Возможно также классифицировать частицы в зависимости только от размера. Напомним, что размер средней по величине молекулы или атома составляет ~ 0,1 нм. На сегодняшний день не существует точного определения того, насколько большим должен быть молекулярный кластер, чтобы превратиться в частицу, но частицы радиуса порядка 1 нм = 10–7см (концентрация таких частиц обычно измеряется при помощи расширительных камер, первая конструкция которых была предложена Айткеном, поэтому частицы называются ядрами, или частицами, Айткена) были измерены экспериментально и, по мнению ряда авторов, представляют собой наименьшие по размеру частицы, которые могут быть обнаружены с помощью расширительных камер. Частицы таких размеров в значительной степени подвержены броуновскому движению, что позволяет им достичь стенок любой камеры разумных размеров в течение нескольких секунд или, в крайнем случае, минут. Поэтому для них трудно отобрать представительную пробу, при консервации проб наблюдаются значительные потери. Частицы малых размеров очень быстро коагулируют с частицами больших размеров. При рассмотрении судьбы частиц следует иметь в виду, что частицы, достигшие стенок камеры, остаются на них вследствие действия сил адгезии. Это отличает поведение частиц от поведения молекул, однако классификация на такой основе не получила развития из-за малой изученности природы адгезионных взаимодействий. Размер порядка 10–6 см характеризует частицы более стабильные, для них коагуляция при атмосферных условиях протекает достаточно медленно, поэтому консервация проб возможна. Из экспериментальных методов для прямых наблюдений за такими частицами обычно используют электронную микроскопию. Частицы размером 10–5см называют «большими» (в контексте атмосферных аэрозолей). На такие аэрозоли одинаково слабое воздействие оказывают как броуновское движение, так и гравитационное осаждение. Частицы таких размеров, по-видимому, характеризуются наибольшим временем жизни. Интересно отметить, что «большие» частицы трудно получить непосредственно как при измельчении твердого тела (обычно размеры частиц при самом тонком помоле больше), так и при конденсации из газовой фазы (за исключением случая наиболее летучих соединений, размер образующихся частиц меньше). Размер 10–4см (1 мкм) – это, на жаргоне специалистов по атмосферным аэрозолям, «хвост» фракции «гигантских» частиц в атмосфере. Скорость падения под действием силы тяжести частиц размером 1 мкм приблизительно равна 2 . 10–2 см . с–1, но даже такое медленное осаждение за 1 сутки составляет уже 20 м. Скорость оседания возрастает пропорционально квадрату радиуса частицы для частиц таких размеров. Такие частицы легко наблюдать на поверхности при небольшом увеличении, но точно измерить их трудно. Размер 10–3см (10 мкм) – это приблизительный размер ядер облака, которые представляют собой очень важную специальную подгруппу атмосферных аэрозолей. Скорость падения такой частицы плотностью 2 г/см3 при нормальных условиях составляет 2см . с–1, поэтому в течение нескольких минут в стандартной комнате большинство таких частиц осело бы на пол. Частицы таких размеров можно увидеть невооруженным глазом на контрастной поверхности, а их размеры могут быть определены с помощью обычного оптического микроскопа. Размер 10–2см (100 мкм) – это размер капель измороси (скорость оседания = 100 см . с–1). Повседневный опыт показывает, что в хорошую погоду частицы таких размеров в атмосфере отсутствуют или очень редки, за исключением пыльных бурь и других подобных явлений, антропогенных или природных. Частицы таких размеров характерны для морских аэрозолей, но быстро оседают и практически не наблюдаются далеко от источника образования. Размер 10–1см (1мм) – типичный размер дождевых капель. В атмосфере в год образуется приблизительно 4 . 1022 дождевых капель, что составляет 10 капель на 1 см2 поверхности Земли. В среднем дожде, однако, их объемная концентрация невелика – 10–5см–3 (или 10 капель на 1 м3 воздуха). В нижних слоях атмосферы средняя концентрация меньше на два порядка. Размер 1 см: падающие капли дождя из-за гидродинамических эффектов разбиваются до диаметра 0,5 см, поэтому жидких аэрозолей размером 1 см не наблюдается, однако град и снежинки (твердые гидрометеориты) могут достичь таких размеров. Размер 10 см: имеются сообщения о граде такого размера, легко оценить масштабы наносимого им вреда. Размер > 10 см: можно сказать, что 10 см — верхний предел размеров атмосферных частиц; конечно, метеориты и частицы пепла при извержении вулканов могут достигать и больших размеров. Итак, даже самая краткая классификация по размерам занимает область от 10–8см до 10 см. Если исключить экстремальные случаи, то останется область в шесть порядков – от 10–7см до нескольких миллиметров. Если перейти к массовым или объемным характеристикам, то получится разброс в 20 порядков, а для такой характеристики, как концентрация, ситуация еще более впечатляющая. Важно представлять себе, что область от 1 мкм до размера молекулы так же велика, как от 1 мкм до градины больших размеров. Поэтому такие макрохарактеристики, как «концентрация частиц аэрозоля» или «средний размер частиц аэрозоля», должны оцениваться очень осторожно. Парниковый эффект
Каждое материальное тело, температура которого выше температуры окружающей среды, как известно, испускает электромагнитное излучение. Чем выше температура тела, тем больше энергия и короче длина волны этого излучения. Поверхность Солнца имеет температуру около 6000 К, и максимальное количество энергии солнечного излучения приходится на длины волн в интервале от 340 до 4000 нм. Для абсолютно черного тела при температурах, характерных для земной поверхности, максимальное количество энергии выделяется с излучением, имеющим длину волны около 10000 нм. Таким образом, Земля поглощает солнечное излучение (преимущественно в видимом диапазоне) и испускает тепло в инфракрасном диапазоне. Поскольку средняя глобальная температура на протяжении последних 10-15 тыс. лет оставалась практически постоянной, можно утверждать, что на планете наблюдался тепловой баланс. Оценка средней температуры Земли, выполненная на основании этого баланса, при условии отсутствия атмосферы вокруг планеты (пример 32) дает значение, отличающееся от реально наблюдаемого более чем на 35 градусов. В случае отсутствия атмосферы температура на планете была бы более чем на 20 градусов ниже 0°С. Однако, являясь смесью газов, атмосфера Земли не излучает в непрерывном диапазоне волн, как абсолютно черное тело. Компоненты атмосферы, молекулы которых содержат три и более атомов в своем составе, – такие, как вода, диоксид углерода и многие другие, интенсивно поглощают излучение в инфракрасном диапазоне, на которое приходится максимальное количество энергии, излучаемой Землей. Водяной пар интенсивно поглощает излучение в диапазоне длин волн 5-7 мкм и более 14 мкм, диоксид углерода – в диапазоне длин волн 4-5 мкм и более 12 мкм. Область длин волн 8-11 мкм не поглощается этими компонентами и является практически прозрачной для излучения Земли. Эту область длин волн называют «окном прозрачности» атмосферы, образно сравнивая его с открытой форточкой, через которую беспрепятственно осуществляется отвод тепловой энергии в окружающее пространство. Увеличение концентрации диоксида углерода в атмосфере, особенно интенсивное в последние 200 лет, приводит к росту эффективности поглощения инфракрасного излучения. В результате этого температура Земли может возрастать. К повышению температуры может привести и увеличение концентрации в тропосфере таких газов, как О3, СН4,N2O,NO2,SO2, фреонов. Эти газы, способные улавливать инфракрасное излучение и частично перекрывать «окна прозрачности» атмосферы, как и диоксид углерода, называют парниковыми газами. Необходимо отметить, что увеличение концентрации аэрозолей в атмосфере и рост альбедо земной поверхности приводят к обратному эффекту – уменьшению температуры в приземном слое. Это явление связано с усилением отражающей способности атмосферы и земной поверхности. Такое возможное резкое снижение температуры, связанное с увеличением запыленности атмосферы при столкновении с астероидом, рассматривается как одна из наиболее вероятных причин гибели динозавров. На климатические последствия, которые могут привести к гибели всего живого, – «ядерную ночь» и следующую за ней «ядерную зиму» – указывают и результаты оценки возможных военных действий с применением ядерного оружия, которые были впервые проведены советскими учеными во главе с Н. Н. Моисеевым. Мелкодисперсные, устойчивые в атмосфере аэрозоли, образующиеся при наземных ядерных взрывах, на длительный промежуток времени могут снизить количество энергии, поступающей на планету, и понизить температуру в приземном слое.
Примеры решения задач
Пример 23. Известно, что окисление оксида азота (NO) может протекать при взаимодействии с молекулярным кислородом и озоном. Рассчитайте время полувыведения оксида азота из приземного слоя атмосферного воздуха и определите, какой из этих процессов вносит основной вклад в окисление NO. Принять, что содержание молекул оксида азота в воздухе в среднем составляет 2 . 109 см–3, а концентрация озона равна 15 млрд–1. Константы скоростей реакций окисления оксида азота кислородом и озоном равны соответственно: kк = 1,93 . 10–38см6 . мол.–1 . с–1 и k0 = 1,8 . 10–14см3 . мол.–1 . с–1. Температура воздуха 15°С, давление 101,3 кПа. Решение. Определим время полувыведения оксида азота из воздуха при его взаимодействии с молекулярным кислородом. Процесс окисления в рассматриваемом случае описывается уравнением: 2NO + O2 = 2NO2 Скорость процесса окисления NO равна: uNO=kк[O2][NO]2, где uNO – скорость процесса окисления NO, см–3 . c–1; kк – константа скорости реакции третьего порядка, см6 . с–1; [J2] и [NО] – концентрации кислорода и оксида азота в воздухе, см–3. Часто, как говорилось ранее, для упрощения записи размерностей констант скоростей химических реакций второго порядка – cм3 . мол.–1 . с–1 – и третьего порядка – см6 . мол.–1 . с–1 — слово «молекула» («мол.») опускается, и тогда эти размерности можно записать как см3 . с–1 и см6 . с–1. Концентрация молекул кислорода в приземном слое воздуха равна 20,95% (об.), что составляет (Пример 8): [О2] = 2,55 . 1019 – 20,95/100 = 5,34 . 1018 (см–3). Поскольку количество молекул кислорода в воздухе значительно превосходит количество молекул оксида азота, можно считать, что концентрация О2 в процессе окисления NO практически не изменяется. Поэтому скорость реакции окисления оксида азота можно представить как скорость реакции псевдовторого порядка уравнением:
где k/к = kк[О2] = 1,93 . 10–38 . 5,34 . 1018 . 10,31 . 10–20 (см3 . с–1) Для реакций второго порядка время (период) полувыведения, т.е. время, за которое концентрация исходных реагентов снизится вдвое, при условии равенства исходных концентраций реагентов определяется по уравнению: t1/2=1/(kC) где k – константа скорости реакции второго порядка, см3 . с–1; С – концентрация исходного реагента, см–1. В рассматриваемом случае для реакции псевдовторого порядка имеем:
t1/2 = 1/(10,31 . 1–20 . 2 . 109) = 4,8 . 109 (с) = 150 (лет) Определим время полувыведения оксида азота из приземного слоя воздуха при его взаимодействии с озоном. В этом случае уравнение реакции окисления NO имеет следующий вид: NO + O3 ® NO2 + O2 Скорость реакции можно рассчитать по уравнению: u/NO = k0[NO][O3] где u/NO – скорость процесса окисления оксида азота озоном, см–3 . с–1; k0 – константа скорости реакции второго порядка, см3 . с–1; [NO] и [О3] – концентрации оксида азота и озона в воздухе, см–3. По условию задачи, концентрация молекул озона в приземном воздухе равна 15 млрд–1; в см-3 это составит (пример 4): [О3] = 2,55 . 1019 . 15 . 10–9 = 3,82 . 1011 (см–3), где 10–9 – коэффициент перевода млрд-1 в объемные доли. Поскольку концентрация озона более чем в сто раз превышает концентрацию оксида азота, можно принять, что в процессе окисления NO значение концентрации озона практически не изменится. В этом случае скорость реакции можно представить как скорость реакции псевдопервого порядка:
где
Для реакций первого порядка время полувыведения реагента определяется по уравнению: t1/2 = 0,693/k где k – константа скорости реакции первого порядка. В рассматриваемом случае для реакции псевдопервого порядка имеем: t1/2 = 0,693/k = 0,б93/(6,88 . 10–3) = 100 (с) = 1,7 (мин) Время полувыведения оксида азота в процессе его взаимодействия с кислородом воздуха значительно больше, чем при взаимодействии NOс озоном, и не соответствует реально наблюдаемым в приземном воздухе процессам превращения оксида и диоксида азота. В атмосферном воздухе время полувыведения оксида азота обычно составляет несколько минут. Поэтому можно утверждать, что в приземном слое воздуха процесс окисления оксида азота связан в основном со взаимодействием с озоном. Ответ: время полувыведения оксида азота при его взаимодействии с кислородом и озоном составляет 150 лет и 1,7 мин соответственно. В приземном воздухе процесс окисления NO в основном протекает при участии озона. Пример 24. Какое максимальное количество молекул озона может образоваться в каждом кубическом сантиметре приземного воздуха при полном окислении метана в присутствии оксидов азота, если концентрация метана уменьшилась с 20 до 1,6 млн–1 . Давление равно 101.3 кПа, температура воздуха 288 К. Решение. При полном окислении метана в присутствии оксидов азота цепочку превращений можно представить следующим суммарным уравнением реакции (уравнение 129): СН4 + 8О2 + 4М ® СО2 + 2Н2O+ 4М* + 4О3 Таким образом, при полном окислении каждой молекулы метала в присутствии оксидов азота может образоваться до 4 молекул озона. При уменьшении концентрации метана в воздухе с 20 до 1,6 млн–1 концентрация образовавшегося озона при отсутствии его стока может составить: [О3] = 4 . (20 – 1,6) = 73,6 (млн–1) Таким образом, в каждом кубическом сантиметре воздуха может образоваться n(O3) молекул озона:
где NA – число Авогадро; a(Оз) – объемная доля озона в воздухе: a(O3) = [О3] . 10–6, млн–1; Vм – молярный объем газа при нормальных условиях, л; Т0 и ТЗ– температура воздуха при нормальных условиях и средняя у поверхности Земли (273 и 288 К соответственно); n(О3) = 6,02 . 1023 . 73,6 . 10–6 . 273/(22,4 . 103 . 288) =19 . 1014 (см–3) Ответ: в каждом кубическом сантиметре воздуха может образоваться до 19 . 1014 молекул озона. Пример 25. Сравните скорости выведения из атмосферы молекул метана при их взаимодействии с гидроксидным радикалом на высотах 5 и 35 км. Концентрация метана изменяется от 2 млн–1 на высоте 5 км до 0,6 млн–1 на высоте 35 км. Энергия активации и предэкспоненциальный множитель константы скорости реакции взаимодействия метана с ОН-радикалом равны 14,1 кДж/моль и 2,3 см3 . с–1 соответственно. Концентрации гидроксидных радикалов соответствуют средним для этих высот значениям: [ОН]5 = 8,5 . 105 см–3 и [ОН]35 = 3 . 107см–3. Решение. В процессе взаимодействия молекул метана с гидроксидным радикалом происходит образование воды и метильного радикала: СН4 + ОН ® СН3 + Н2О Скорость реакции можно определить из уравнения: uH = kH[CH4]H[OH]H, где uH и kH – скорость и константа скорости реакции для условий, характерных для атмосферного воздуха на высоте H; [СН4]H и [ОН]H – концентрации молекул метана и гидроксидного радикала на высоте H. В соответствии с уравнением Аррениуса константа скорости химической реакции зависит от температуры: k = Ae–E/RT где k – константа скорости химической реакции (размерность определяется единицами измерения концентрации и времени, а также порядком химической реакции); А – предэкспоненциальный множитель (имеет размерность константы скорости реакции); Е – энергия активации реакции, Дж/моль; R – универсальная газовая постоянная, Дж/ (моль . К); Т – температура реакции, К. В рассматриваемом случае скорость химической реакции будет определяться значениями концентраций реагентов и температурой воздуха на заданных высотах. Температура воздуха на высоте 5 км составляет (пример 8) T5 = 288 + (–6,5 . 5) = 256 (К), на высоте 35 км она равна: Т35 = 217 + (35 –11) . 1,38 = 250 (К) Константа скорости реакции на высоте 5 км составляет k5 = 2,3 ехр[–14,1 . 103/(8,31 . 256)] = 3,04 . 10–3 (см3 . с–1), а на высоте 35 км k35 = 2,3ехр[–14,1 . 1000/(8,31 . 250)] = 2,59 . 10–3 (см3 . с–1) Для расчета скорости химической реакции необходимо привести значения концентраций реагентов и константы скорости к одинаковым единицам измерения. Переведем заданные в условиях задачи значения концентраций молекул метана в см–3: [СН4]H = СH(млн–1) . NH (см–3) . 10–6, где 10–6 – коэффициент пересчета концентрации, выраженной в млн–1 в объемные доли; NH – количество молекул в см3 воздуха на заданной высоте. Количество молекул в см3 воздуха на высоте 5 км можно определить по уравнению: N5 = 2,55 . 1019 ехр[Мq . 5000/(R . 256)], где 2,55 . 1019 – количество молекул в кубическом сантиметре воздуха на уровне моря, см–3; М – средняя молярная масса воздуха, равна 28,96 . 10–3 кг/моль (пример 7); q – ускорение свободного падения, равно 9,8 м/с2; 5000 – высота над уровнем моря, м; R – универсальная газовая постоянная, равна 8,31 Дж/(моль . К); 256 – температура воздуха на высоте 5 км, К; N5 = 2,55 . 1019ехр[–28,96 . 10–3 . 9,8 . 5000/(8,31 . 256)] = 1,31 . 1019 (см–3) Количество молекул в см3 воздуха на высоте 35км составит: N35 = 2,55 . 1019ехр[–29 . 10–3 . 9,8 . 35000/(8,31 . 250)] = 2,12 . 1017(см–3) Количество молекул метана в см3 на высоте 5 км составит [СН4]5 = 2 . 1,31 . 1019 . 10–6 = 2,62 . 1013 (см–3), а на высоте 35км [СН4]35 = 0,6 . 2,12 . 1017 . 10–6 = 1,27 . 1011 (см–3) Скорость химической реакции на высоте 5 км составит u5 = 3,04 . 10–3 . 2,62 . 1013 . 8,5 . 105 = 6,77 . 1016 (см–3 . с–1), а на высоте 35 км u5 = 2,59 . 10–3 . 1,27 . 1011 . 3 . 107 = 9,86 . 1015 (см–3 . с–1). Отношение скоростей химических реакций взаимодействия метана с гидроксидным радикалом составит: u5/u35 = 1,27 . 1016/(9,86 . 1015) = 12,88 Ответ:Скорость процесса вывода метана из атмосферы при его взаимодействии с гидроксидным радикалом на высоте 5 км в 13 раз выше, чем на высоте 35 км.
Пример 26.Определите соотношение скоростей процессов газофазного и жидкофазного окисления SO2 при условии, что основной вклад в эти процессы вносят следующие реакции: SO2(r) + OH(r) ® HSO3(r) (1) SO2(p-p) + H2O(p-p) ® H2SO4(p-p) (2) Константы скоростей реакций окисления равны: k1 = 9 . 10–13см3 . мол.–1 . с–1; k2 = 1 . 103 л . моль–1 . с–1. Концентрации примесей в газовой фазе составляют: [ОН] = 5 . 106 см–3; [SO2] = 10–4% (об.); [Н2О2] = 10–7% (об.) Расчеты провести для атмосферного воздуха, имеющего температуру 25°С и содержащего: а) 0, б) 0,0001, в) 0,01 г свободной воды в каждом литре воздуха. Считать, что при растворении в воде концентрация SO2 в газовой фазе не меняется. Газы считать идеальными и подчиняющимися закону Генри. Давление принять равным 1 атм. Решение.Скорость окисления 302 в газовой фазе можно определить по уравнению: u1 = k1[OH][SO2] где k1 – константа скорости реакции; [ОН] и [SО2] – концентрации реагентов в газовой фазе. Для определения скорости реакции переведем размерность концентрации SО2 из объемных процентов в см–3: [SO2] (см–3) = [SО2][%(об.)] . NAT0/(100VмT1) = = 10-4 . 6,02 . 1023 . 273/(100 . 22,4 . 103 . 298) = 2,46 . 1013 (см–3) Скорость газофазного окисления составит: u1 = 9 . 10–13 . 5 . 106 . 2,46 . 1013 = 1,1 . 108 (см–3 . с–1) В случае отсутствия свободной (капельножидкой) воды в атмосфере (вариант «а») окисление в жидкой фазе происходить не может, и скорость процесса полностью определяется скоростью газофазного окисления. В случае присутствия капельножидкой воды в воздухе окислению в жидкой фазе предшествует растворение газов в воде. Концентрацию компонентов в растворе, в соответствии с законом Генри, можно определить по уравнению: Ci = КГiРi где Ci – концентрация i-го компонента в растворе; КГi – значение константы Генри для i-го компонента (приводятся в справочной литературе); Рi – парциальное давление i-го компонента в газовой фазе. Окислению SО2 в жидкой фазе предшествует растворение SO2 и Н2О2 в воде. Константы Генри для этих газов при 25°С составляют (таблица 3 Приложения): КГ(SO2) = 5,4 моль/(л . атм) КГ(H2O2) = 1 . 105моль/(л . атм) Парциальное давление легко найти, зная объемную долю соответствующего компонента в газовой фазе и общее давление воздуха: Р(SО2) = 10–4 . 10–2 . 1 = 10–6 (атм) Р(Н2O2) = 10–7 . 10–2 . 1 = 10–9 (атм) Концентрации компонентов в растворе составят: [SО2] = 5,4 . 10–6 (моль/л) [Н2О2] = 1 . 105 . 10–9 = 10–4 (моль/л) Скорость процесса окисления SO2 в жидкой фазе можно определить по уравнению: u2 = k2[SO2][H2O2]; u2 = 1 . 103 . 5,4 . 10-6 . 10-4 = 5,4 . 10–7 [моль/(л . с)] Полученное значение скорости окисления SO2 в жидкой фазе показывает, что в каждом литре раствора в секунду будет окисляться 5,4 . 10–7 молей SO2. Эту величину трудно сравнить с полученным выше значением скорости окисления SO2 в газовой фазе, которое показывает количество молекул, окисляющихся в каждом кубическом сантиметре воздуха в секунду. Поэтому, зная содержание свободной воды в воздухе и принимая плотность раствора равной плотности воды, приведем значение скорости окисления SO2 в жидкой фазе к сопоставимым единицам измерения: u2[мол/(см3 . с)] = u2[моль/(л . c)]nNA/g где n– содержание капельножидкой воды в воздухе, г (воды)/см3 (воздуха); NA – число Авогадро; g –плотность воды, г/л. Подставив соответствующие численные значения, получим зависимость скорости окисления от содержания влаги в воздухе: u2 = 5,4 . 10–7n . 6,02 . 1023/1000 = 32,5 . 1013n В случае, когда содержание воды в воздухе n = 0,0001 г/л (вариант «б»), соотношение скоростей окисления SO2 в газовой и жидкой фазах составит: a = u1/u2 = 1,1 . 108/(3,25 . 1014 . 0,0001 . 10–3) = 3,4 В случае n = 0,01 г/л (вариант «в») это соотношение будет: a =u1/u2 = 1,1 . 108/(3,25 . 1014 . 0,01 . 10–3) = 0,034 Ответ: а) при отсутствии капельножидкой воды в воздухе скорость окисления диоксида серы определяется процессом окисления в газовой фазе; б) при содержании влаги в воздухе, равном 0,0001 г/л, скорость окисления SO2 в газовой фазе будет превышать скорость жидкофазного окисления в 3,4 раза; в) при содержании влаги в воздухе, равном 0,01 г/л,окисление будет протекать с большей скоростью в жидкой фазе; в этом случае соотношение скоростей окисления SO2 в газовой и жидкой фазах будет равно 0,034. Пример 27.Константа равновесия реакции образования оксида азота из азота и кислорода при 800 К равна 3 . 10–11. Какого равновесного значения может достигнуть концентрация оксида азота в смеси, если исходная смесь – воздух?
Решение.Процесс образования молекул оксида азота из азота и кислорода воздуха может быть представлен следующим уравнением: N2 + О2 ® 2NO Поскольку в процессе образования оксида азота не происходит изменения количества молей газов в смеси, константы равновесия при постоянном давлении и постоянной концентрации Кр и КC равны, и нет необходимости в дополнительных пояснениях в условиях задачи. Константу равновесия реакции можно представить уравнением: Кр = P(NO)2/[P(N2) . Р(О2)], где P(NO), P(N2) и Р(О2) – парциальные давления NO, N2 и О2. Ниже представлены равновесные значения парциального давления компонентов смеси в кПа:
* Парциальные давления азота и кислорода соответствуют значениям, характерным для сухого воздуха при нормальном атмосферном давлении. Поскольку константа равновесия процесса образования оксида азота мала, можно предположить, что равновесные значения парциального давления NO будут низкими, поэтому парциальные давления азота и кислорода практически не изменятся. В связи с этим при расчете можно воспользоваться приближенными равновесными значениями парциальных давлений компонентов смеси: 3 . 10–11 = 4х2/(79,12 × 22,23), 2х = Р(NO) = 22,97 . 10–5 (кПа) = 0,23 (Па) Ответ: в воздухе при температуре 800 К парциальное давление оксида азота составит 0,23 Па.
Пример 28. Оцените мольное соотношение и общую массу диоксида серы и оксида азота, поступающих в атмосферу в течение суток с выбросами тепловой электростанции, работающей на угле. Содержание серы в угле равно 1,5% (мас.) В сутки на станции сжигается 10 тыс. т угля. Концентрация оксида азота в газовых выбросах оставляет 150 млн–1. Для сжигания угля используется стехиометрически необходимое количество воздуха. При оценке принять, что уголь состоит из углерода и содержит в качестве примеси только серу. Решение: Появление диоксида серы в выбросах отходящих газов при сжигании топлива связано с процессом окисления соединений серы, присутствующих в исходном топливе. В рассматриваемом случае процесс можно представить уравнением: S + O2 ® SO2 Количество серы, сжигаемое на станции за сутки, составит: m(S) = m(угля) . a(S), где m(S) и m(угля) – массы серы и угля, сжигаемого на станции в сутки; a (S) – весовая доля серы в угле; m(S) = 10000 . 0,015 = 150 (т/сут) Количество долей диоксида серы, образующегося в процессе горения угля, равное количеству молей серы, содержащейся в угле, составит: N(SO2) = N(S) = m(S)/M(S), где M(S) – молярная масса серы, г/моль; N(SO2)= 150 . 106/32 = 4,69 . 106 (моль/сут) Для вычисления количества молей оксида азота, образующегося в процессе горения угля, необходимо найти общее количество молей газов, содержащееся в отходящих продуктах (NОбщ). Эта величина будет определяться количеством молей азота, содержащегося в воздухе, необходимом для окисления углерода и серы из угля, – N(N2), количеством молей диоксида углерода, образующегося при горении углерода, – N(СО2) и количеством молей образующегося диоксида серы – N(SO2): Nобщ = N(N2) + N(СО2) + N(SO2) Процесс окисления углерода можно представить уравнением: С + О2 ® СО2 Каждые сутки на станции сжигается 10000 т угля, которые по условию задачи содержат 150 т серы и 9850 т углерода. Количество молей углерода, сжигаемого на станции в сутки, составит: N(С) = m(С)/М (С), где М(С) – молярная масса углерода, г/моль; N(C) = 9850 . 106/12 = 8,21 . 108 (моль/сут) На каждый моль углерода образуется моль диоксида углерода и расходуется, как и при окислении серы, один моль кислорода из воздуха. Поэтому количество молей диоксида углерода, образовавшегося в процессе горения угля, составит: N(СО2) = N(C) = 8,21 . 108 (моль/сут) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
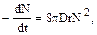 (132)
(132) (135)
(135)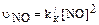
 – константа скорости реакции псевдовторого порядка, см3 . мол.–1 . с–1;
– константа скорости реакции псевдовторого порядка, см3 . мол.–1 . с–1;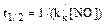
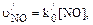
 – константа скорости псевдопервого порядка;
– константа скорости псевдопервого порядка;