
|
|
Состав и строение атмосферыФИЗИКО-ХИМИЧЕСКИЕ ПРОЦЕССЫ В АТМОСФЕРЕ Учебное пособие
САРАТОВ - 2006
ББК 20.1 я 73
Т.Г. Дмитриенко
Учебное пособие по химии окружающей среды охватывает вопросы физико-химических процессов, происходящих в атмосфере, и подготовлено традиционным способом: включает теоретическое введение, примеры решения типовых задач и задачи для самостоятельного решения. Пособие содержит вопросы и задачи для самостоятельной подготовки к учебному модулю, являющимся итоговой оценкой по теме: «Физико-химические процессы в атмосфере». Приводимое в учебном пособии краткое изложение темы курса, примеры решения задач, вопросы для самопроверки и контрольные задачи должны способствовать повышению эффективности самостоятельной работы студентов, являющейся основой успешного образования. Структура пособия соответствует традиционной структуре курса «Химия окружающей среды» и может быть использовано для подготовки к семинарским и практическим занятиям.
Рецензенты: доктор химических наук, профессор Древко Б.И. кандидат химических наук, доцент Ястребова Н.И.
ã Саратовский военный институт радиационной, химической и биологической защиты, 2006
ФИЗИКО-ХИМИЧЕСКИЕ ПРОЦЕССЫ В АТМОСФЕРЕ
Предмет и содержание курса «Химия окружающей среды»
Химия окружающей среды базируется на основных законах и понятиях классической химии, однако объекты исследования в этом случае находятся в биосфере. Необходимо подчеркнуть; что химия окружающей среды как сравнительно молодая область знания в настоящее время интенсивно развивается в нашей стране и за рубежом. Предметом курса «Химия окружающей среды» являются основные физико-химические процессы, протекающие с участием абиотических компонентов биосферы в естественных условиях, и изменения в этих процессах, связанные с влиянием антропогенных факторов. Усиление техногенного воздействия на природную среду вызвало деградацию качества окружающей среды и породило целый ряд связанных с этим проблем, наиболее острая из которых – состояние атмосферного воздуха. По сравнению с другими земными оболочками атмосфера имеет ряд присущих только ей особенностей – высокую подвижность, изменчивость ее компонентов, своеобразие физико-химических процессов. Состояние атмосферы определяет тепловой режим поверхности Земли, ее озоновый слой защищает живые организмы от жесткого ультрафиолетового излучения. Распределение тепла и влаги в атмосфере – основная причина существования природных зон на Земле, определяющих особенности гидрологического режима, состояние почвенно-растительного покрова и важные процессы формирования рельефа. Физико-химические превращения компонентов атмосферы являются важнейшим разделом химии окружающей среды. Специфические особенности этих превращений связаны как с природными (фаза солнечной активности, географическое положение, время суток), так и с антропогенными факторами. Знание механизмов и кинетики образования конечных продуктов реакций необходимо для разработки методов защиты окружающей среды от промышленных загрязнений.
Состав и строение атмосферы Общая масса газовой оболочки нашей планеты – атмосферы – составляет 5,14 . 1015 т. Это примерно одна миллионная часть массы Земли. Состав атмосферы претерпевал серьезнейшие изменения в различные геологические эпохи. В настоящее время состав атмосферы находится в состоянии динамического равновесия, поддерживаемого в результате действия живых организмов, геохимических явлений и хозяйственной деятельности человека. Таблица 1. Состав атмосферы вблизи земной поверхности
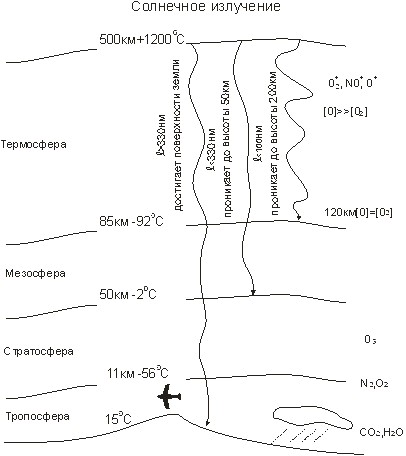
Главными компонентами атмосферы (таблица 1) являются азот, кислород и аргон: на их долю в приземном слое приходится соответст-венно 78,21 и 0,9% (об.). На долю всех остальных компонентов приходится менее 0,1% (об.), но роль их в общей динамике состояния атмосферы чрезвычайно велика. Объемные концентрации постоянно содержащихся в атмосфере (так называемых «квазипостоянных») компонентов (N2, О2, Аr, Не, Хе, Кr, Н2) остаются практически неизменными вплоть до высоты 100 км. Содержание других («активных») газов и аэрозолей существенно меняется в зависимости от сезона, географического положения и высоты над уровнем моря. Антропогенное влияние на состав атмосферы ограничено в основном изменениями концентрации «активных» газов и аэрозолей. Для измерения содержания примесей в атмосфере помимо % (об.) часто используются другие единицы измерения концентрации газообразных компонентов в смеси. Для выражения объемной концентрации широкое распространение получили млн–1 и млрд–1 (в англоязычном варианте – ppm и ррb соответственно). Эти единицы измерения показывают количество объемов данной примеси в одном миллионе или миллиарде объемов газовой смеси. Массовые концентрации примесей определяют массу соответствующей примеси в единице объема газовой смеси. Наиболее часто для выражения массовых концентраций «активных» примесей в газовой фазе используются такие единицы, как мг/м3 или мкг/м3. Содержание примесей в воздухе измеряют и по количеству молекул соответствующих газов в кубическом сантиметре или кубическом метре воздуха – мол./см3 или мол./м3; часто слово «молекула» («мол.») опускается и дается упрощенная запись – см –3 или м –3. Содержание газов и паров в воздухе может быть выражено и их парциальным давлением. В этом случае используются стандартные единицы измерения давления Па или кПа (в СИ). В литературе встречаются и устаревшие единицы измерения давления – атмосфера (атм), миллиметры ртутного столба (мм рт. ст.), бар и торр. Одним из важных показателей, характеризующих поведение примесей в атмосфере, является время их пребывания в рассматриваемом объеме атмосферы. В случае динамического равновесия – равенства скоростей поступления примеси из всех возможных источников и суммарного стока примеси из резервуара – время пребывания примеси и ее общая масса в резервуаре связаны уравнением: Qисточник = Qсток = А/t (1) где Qисточник и Qсток – скорости поступления и стока вещества соответст-венно для произвольного резервуара, атмосферы в целом или ее части (единицы массы/единицы времени); А – общая масса примеси, содержащейся в произвольном резервуаре, атмосфере в целом или в ее части (единицы массы); t – время пребывания примеси в произвольном резервуаре, атмосфере в целом или в ее части (единицы времени). По вертикали атмосфера имеет слоистое строение. Наиболее распространенное деление атмосферы на слои основано на изменении температуры с высотой. По мере удаления от поверхности Земли температура сначала снижается (тропосфера), затем практически не меняется (тропопауза), в дальнейшем начинает повышаться (стратосфера), на определенном участке опять остается практически неизменной (стратопауза), вновь начинает падать (мезосфера), проходит через слой с практически неизменными значениями (мезопауза) и далее увеличивается (термосфера). Представленные в таблице 2 и на рисунке 1 сведения характеризуют температурные границы соответствующих слоев для так называемой «стандартной атмосферы», в которой не принимаются во внимание участки с неизменной по высоте температурой. Безусловно, в реальных условиях границы соответствующих слоев не являются строго фиксированными и меняются в достаточно больших пределах, однако профили температур в слоях остаются неизменными. Использование понятия «стандартной атмосферы» облегчает задачу определения параметров атмосферы на заданной высоте и позволяет провести необходимые оценки.
Рис. 1. Строение атмосферы Таблица 2. Характеристика изменения температуры в основных слоях, выделяемых в атмосфере
Очень часто отдельные слои атмосферы объединяют в две группы. При этом тропосферу и стратосферу относят к «нижним слоям атмосферы», а мезосферу и термосферу объединяют понятием «верхние слои атмосферы». Ионизованная часть верхних слоев атмосферы называется ионосферой. Верхние слои атмосферы по составу образующих их компонентов в значительной степени отличаются от нижних слоев. Нижние слои более плотные, в них сосредоточена основная масса атмосферы; известно, что около 50% общей массы атмосферы приходится на нижний слой толщиной всего 5 км, а масса слоя в 30 км составляет примерно 90% всей массы атмосферы. При нормальных условиях газы, входящие в состав атмосферы, мало отличаются по своему поведению от идеального газа. Поэтому для реальной атмосферы справедлива формула, представляющая собой уравнение состояния идеального газа: P = nkT, (2) где P – давление газа; n – концентрация частиц; k– постоянная Больцмана; Т – температура. Распределение давления в атмосфере по высоте H описывается так называемой «барометрической формулой»: Pн = где r0иP0 – плотность и давление при Н = 0 (т. е. на уровне моря), причем Р0 = 101,3 кПа; g – ускорение силы тяжести. Если выражать высоту в километрах, то барометрическую формулу удобно представить (принимая Т = 273 К) в следующем виде: Pн = P0 exp(–H/7,99), (4) Распределение концентрации составляющих атмосферу компонентов по высоте имеет вид: nH = n0exp[-mqH/(kT)]=n0exp[-MqH/(RT)],(5) где m – масса молекулы компонента; n0 – количество молекул в единице объема на высоте Н = 0 (на уровне моря); k – постоянная Больцмана; М – молярная масса газа; R – универсальная газовая постоянная. Атмосфера Земли, как и атмосферы других планет, не находится в равновесном состоянии. Вследствие этого ее температура не постоянна, а изменяется по высоте. Если бы равновесное состояние было возможно, то плотность атмосферы должна была бы изменяться с высотой по формуле Больцмана, которая принимает в этом случае вид n(r) = n(r0)exp{–[GmM/(kT)] × (1/ro-1/r)}, (6) где учтено выражение для потенциальной энергии U(r)частицы массы m в поле тяготения шарообразного небесного тела массы М: U(r) = где G – гравитационная постоянная; r0 – радиус планеты; r– расстояние от центра планеты до частицы. Формула (6) показывает, что при r ® ¥ плотность стремится к пределу: n(r®¥) ® n(r0)exp{–[GmM/(kT)] × 1/r0} (8) Если в атмосфере имеется конечное число молекул, то они должны быть распределены по всему космическому пространству, т.е. атмосфера рассеяна. Поскольку в конечном счете все системы стремятся к равновесно-му состоянию, то атмосфера планет постепенно рассеивается. У некоторых из небесных тел, например у Луны, атмосфера полностью исчезла, другие, например Марс, имеют очень разреженную атмосферу. Таким образом, атмосфера Луны уже достигла равновесного состояния, а атмосфера Марса близка к достижению равновесного состояния. У Венеры атмосфера очень плотная и, следовательно, находится в начале пути к равновесному состоянию. Для количественного рассмотрения вопроса о потере атмосферы планетами необходимо принять во внимание распределение молекул по скоростям. Силу земного притяжения могут преодолеть лишь молекулы, скорость которых превосходит вторую космическую. Эти молекулы находятся в «хвосте» распределения Максвелла – Больцмана и их относительное число невелико. Тем не менее за значительные промежутки времени потеря молекул является чувствительной. Поскольку вторая космическая скорость у тяжелых планет больше, чем у легких, интенсивность потери атмосферы у массивных небесных тел меньше, чем у легких, т, е. легкие планеты теряют атмосферу быстрее, чем тяжелые. Время потери атмосферы зависит также от радиуса планеты, температуры, состава атмосферы и т. д. Полный количественный анализ этого вопроса является сложной задачей. Примеры решения задач
Пример 1.Во сколько раз будет превышено значение максимально разовой ПДК для уксусной кислоты, равное 0,2 мг/м3, если на складе произошла авария (разлилась кислота) и установилось динамическое равновесие между парами и жидкой уксусной кислотой? Парциальное давление паров уксусной кислоты принять равным 3 Па. Атмосферное давление равно 101,3 кПа, температура 25°С. Решение. Для решения задачи найденную концентрацию уксусной кислоты в воздухе и ПДКм.р. необходимо выразить в одних и тех же единицах измерения и определить их отношение. Определим концентрацию уксусной кислоты в воздухе, сделав допущение о том, что пары уксусной кислоты являются идеальным газом. Поскольку известно, что уравнение состояния идеального газа применимо к смесям так же, как и к индивидуальным газам, то можно записать: C = n/V = P/(RT), где С – концентрация паров уксусной кислоты, моль/л; n –количество молей уксусной кислоты в объеме V; Р–парциальное давление паров уксусной кислоты, кПа; R – универсальная газовая постоянная, R = 8,12л-кПа/(моль . К); Т – температура воздуха, К; C = 3 × 10–3/(8,12 × 298) = 1,23 × 10–6(моль/л). Выразим полученное значение концентрации в мг/м3: С/(мг/м3) = С (моль/л) М × 103 × 103, где М – молярная масса, г/моль (для уксусной кислоты М= 60г/моль); 103 – коэффициент перевода граммов в миллиграммы; 103 – коэффициент перевода литров в кубические метры. С/ = 1,23 × 10–6 × 60 × 106 = 74,4 (мг/м3) Определим отношение концентрации уксусной кислоты в воздухе к ПДКм.р.: а = С//ПДКм.р. = 74,4/0,2=370 Ответ:концентрация паров уксусной кислоты превысит значение ПДКм.р. в 370 раз. Пример 2. Превышается ли и если да, то во сколько раз значение максимально разовой ПДК для аммиака, равное 0,2 мг/м3, при обнаружении его запаха, если порог обнаружения запаха для аммиака составляет 46,6 ррm? Атмосферное давление равно 100 кПа, температура 25°С. Решение.Для ответа на вопрос необходимо привести концентрацию, соответствующую порогу обнаружениязапаха, и ПДК.м.р. к одинаковым единицам измерения и найти их отношение. Выразим концентрацию аммиака в мг/м3: С/ = С//МТ0Р/(VmТР0), где С/и С// – концентрация аммиака, выраженная в мг/м3 и ррm соответственно; М – молярная масса аммиака (17 г/моль); Vm – объем, занимаемый одним молем газа при нормальных условиях (температура Т0 = 273К, давление P0 = 101,3кПа), Vm= 22,4л; Ти Р – температура (К) и давление воздуха (кПа) в рассматриваемых условиях; С/ = 46,6 × 17 × 273 × 100/(22,4 × 298 × 101,3) = 32,0(мг/м3) Найдем отношение концентрации аммиака при обнаружении запаха и ПДКм.р.: а = С//ПДКм.р = 32,0/0,2 = 160. Ответ:при обнаружении запаха аммиака его концентрация в воздухе в 160 раз превысит значение ПДКм.р..
Пример 3. Сколько молекул формальдегида присутствует в каждом кубическом сантиметре воздуха при нормальных условиях, если его концентрация достигает значения ПДКм..р.., равного 0,035 мг/м3? Решение. Определим число молей формальдегида в кубическом метре воздуха: С = C//(M × 103), где Си С/ – концентрация формальдегида в воздухе, выраженная в моль/м3 и мг/м3 соответственно; М– молярная масса формальдегида (30 г/моль); 103 – коэффициент перевода граммов в миллиграммы. Число молей формальдегида в 1 м3 воздуха при концентрации, равной ПДКм.р, составит: С = 0,035/(30 × 103) = 1,17 × 10–6 (моль/м3) Число молекул формальдегида в кубическом сантиметре воздуха – N (см–3) – можно определить по уравнению: N = C × 10–6 × NA где С – концентрация формальдегида в воздухе, моль/м3; NA – число Авогадро, мол./моль; 10–6 – коэффициент перевода м3 в см3. N = 1,17 × 10–6 × 10–6 × 6,02 × 1023 = 7,0 × 1011 (см–3) В размерности N (мол./см3) слово «молекула» («мол.») обычно опускается, и размерность записывается как см–3. Ответ:при концентрации формальдегида, равной ПДКм.р., в каждом кубическом сантиметре воздуха присутствует 7,0 × 1011 молекул СН2О. Пример 4. В восьмидесятых годах 20-го века среднегодовая концентрация диоксида углерода в атмосфере, приведенная к температуре 273 К и давлению воздуха 101,3 кПа, достигла 340 млн–1. Определите значения концентрации СО2 в % (об.), см–3, моль/л, мг/м3 и парциальное давление СО2 в Па при средней температуре воздуха вблизи поверхности Земли. Решение.Выразим концентрацию СО2 %(об.) – С///: С/// = С// × 10–4, где С// – концентрация СО2, выраженная в млн–1, или ррm; 10–4 – коэффициент перевода млн–1 (или ррm) в %(об.); С/// = 342 × 10–4% (об.)= 0,034% (об.). При нормальных условиях (температура 0°С, давление – 101,3 кПа) в каждом кубическом сантиметре газа содержится 2,69 × 1019 молекул (эту величину часто называют числом Лошмидта). Это число получается при делении общего числа молекул в 1 моле любого газа (числа Авогадро) на объем Vм, занимаемый этим количеством газа (мольный объем газа), выраженный в см3: N0 = NA/VM = 6,02 × 1023/(22,4 × 103) = 2,69 × 1019(cм–3) Поскольку мольный объем газа меняется в зависимости от температуры и давления газа, при температуре Ти атмосферном давлении Рчисло молекул в кубическом сантиметре любого газа составит: NT = N0T0P/(TP0), где NTиN0– числа молекул в кубическом сантиметре любого газа при заданных и нормальных условиях соответственно; Т0, P0 и T, Р– температура и давление при нормальных и заданных условиях соответственно. При 15°С (288 К) и нормальном атмосферном давлении общее количество молекул идеального газа или смеси идеальных газов в одном кубическом сантиметре составит: N288 = 2,69 × 1019 × 273 × 101,3/(288 × 101,3) = 2,55 × 1019(см–3) Количество молекул диоксида углерода в кубическом сантиметре воздуха, (Nд.у) при условии, что воздух и диоксид углерода ведут себя как идеальные газы, можно определить, зная его объемную долю: Nд.у. = N288C*, где С* — объемная доля диоксида углерода в воздухе; Nд.у = 2,55 × 1019 × 3,4 × 10–4 = 8,7 × 1015 (см–3) Определим парциальное давление диоксида углерода в воздухе. Значения объемных концентраций примесей приводятся обычно в пересчете на сухой воздух; при определении парциального давления в реальных условиях следует учитывать парциальное давление паров воды, которые всегда присутствуют в атмосферном воздухе. Поэтому рекомендуется пользоваться следующим уравнением: P = (Pвозд. – Pводы)C////100, где Р– парциальное давление примеси, кПа; Рвозд. – атмосферное давление, кПа; Рводы – давление паров воды, кПа; С/// – концентрация примеси, % (об.); 100 – коэффициент перевода % (об.) в доли. Однако, поскольку в условиях задачи отсутствуют данные о парциальном давлении паров воды в воздухе, проведем упрощенный расчет: P = Pвозд. C////100, Р = 101,3 × 3,4 × 10–2/100= 3,46 × 10–2 (кПа) =35 (Па) Количество молей диоксида углерода в литре воздуха определим по уравнению (пример 1): Сд..у. = P/(RT), где С– концентрация диоксида углерода, моль/л; Сд.у. = 3,46 × 10–2/(8,12 × 288) = 1,5 × 10–5 (моль/л) Количество мг диоксида углерода в кубическом метре воздуха составит: C/д.у. = C/д.у. × 106 где М – молярная масса СО2, г/моль; С/ = 1,48 × 10–5 × 44 × 106 = 650 (мг/м3) Ответ:концентрация диоксида углерода в воздухе составит: 0,034% (об.); 8,7 × 1015см–3; 1,5 × 10–5 моль/л; 650мг/м3; парциальное давление диоксида углерода равно 35 Па.
Пример 5. При одновременном присутствии СО и О2 во вдыхаемом воздухе в крови устанавливается равновесное отношение концентраций карбоксигемоглобина и оксигемоглобина, которое пропорционально отношению парциальных давлений газов: [СОНb]/[02Нb] = КРСО/РО2. Коэффициент пропорциональности Кдля крови человека изменяется в пределах от 200 до 250. Содержание оксида углерода в сигаретном дыме составляет 400-450 млн–1. Какое среднее содержание карбоксигемоглобина может наблюдаться в организме курильщика, который дышит сигаретным дымом, если содержание кислорода в табачном дыме соответствует средним для приземного воздуха значениям? К каким последствиям это может привести, если известно, что при контакте с гемоглобином крови человека оксид углерода образует карбоксигемоглобин СОНb, при этом снижается доля гемоглобина, связанного с кислородом (оксигемоглобина – О2Нb), и нарушается кислородный обмен в организме? При концентрации карбоксигемоглобина в крови, равной 2-5%, наблюдается поражение центральной нервной системы, выражающееся в нарушении ряда психомоторных функций. При содержании СОНb в крови более 5% происходят функциональные изменения сердечной и легочной деятельности. В случае содержания СОНb в крови 10-80% наблюдаются головные боли, спазмы, респираторные нарушения, может наступить смерть. Решение. Парциальное давление оксида углерода в сигаретном дыме PСО можно определить по уравнению: PCO = PобщaCO, где Рoбщ – общее давление смеси (по условию задачи равно давлению воздуха, при нормальных условиях – 101,3 кПа); aCO – объемная доля оксида углерода в табачном дыме (примем среднее значение из интервала концентраций СО aCO = 425 . 10–6); РСО = 101,3 . 425 . 10–6 = 4,30 . 10–2 (кПа) Парциальное давление кислорода в табачном дыме по условию задачи равно парциальному давлению кислорода в приземном воздухе и без учета содержания паров воды в воздухе составляет: Ркисл = 101,3 . 0,2095 = 21,2 (кПа) Принимая значение коэффициента пропорциональности в уравнении, связывающем отношение концентраций карбоксигемоглобина и оксигемоглобина в крови человека с отношением парциальных давлений газов, равным 225, определим среднее отношение карбоксигемоглобина и оксигемоглобина в крови человека, вдыхающего табачный дым: [СОНb]/[О2Нb] = К . Pсо/Pо2 = 225 . 4,30 . 10–2/21,2 = 0,456 Примем процентное содержание гемоглобина, связанного с оксидом углерода (карбоксигемоглобина), в крови курильщика, вдыхающего табачный дым, за Х%. Тогда содержание оксигемоглобина составит [O2Нb] = (100 – Х)%,а их отношение можно выразить уравнением: [СОНb]/[02Нb] = X/(100 – X) = 0,456 Решая это уравнение, найдем X = 31%. Таким образом, среднее содержание карбоксигемоглобина в крови курильщика, вдыхающего табачный дым, составит 31%. Это значение находится в интервале от 10 до 80%, поэтому будут наблюдаться головные боли, спазмы, респираторные нарушения, может наступить смерть. Ответ: среднее содержание карбоксигемоглобина в организме курильщика, который дышит сигаретным дымом, составит 31%. У курильщика, вдыхающего табачный дым, будут наблюдаться головные боли, спазмы, респираторные нарушения, может наступить смерть. Пример 6. Следует ли ожидать выпадения росы летним вечером, если температура снизилась с 30°С в 12 ч дня до 15°С? В полдень относительная влажность воздуха составляла j = 40%. Решение. Для решения задачи необходимо воспользоваться справочными данными о влажности воздуха. Равновесное парциальное давление паров воды в воздухе равно (таблица 2 Приложения): при 30°С Рабс = 0,04187 атм; при 15°С Рабс = 0,01683 атм. Определим парциальное давление паров воды в полдень: Р(30°С) = Р(30°С)абс . j; Р(30°С) = 0,04187 . 40/100 = 0,01675 (атм) Сравним полученное значение с равновесным парциальным давлением паров воды при 15°С: Р(30°С) = 0,01675 атм < 0,01683 атм = Р(15°С)абс Следовательно, пары воды конденсироваться не будут, роса не образуется. Ответ:выпадания росы не произойдет. Пример 7.Масса атмосферы оценивается величиной 5 . 1015 т. Определите количество кислорода в атмосфере в кг в допущении, что атмосфера состоит только из таких «квазипостоянных» компонентов, как азот, кислород и аргон, а их объемная концентрация соответствует значениям, характерным для приземного слоя атмосферы (таблица 1). Решение.Для решения задачи на первом этапе необходимо определить среднюю молярную массу смеси газов, т. е. среднюю молярную массу воздуха Мвозд.: Мвозд. = Мазот . aазот + Мкисл . aкисл + Марг . aарг где Мазот, Мкисл и Марг – молярная масса азота, кислорода и аргона соответственно; aазот, aкис и aарг – объемные доли соответствующих компонентов смеси в воздухе (таблица 1) Мвозд. = 28,01 . 0,7810 + 32,00 . 0,2095 + 39 . 0,0095 = 28,96 (г/моль) Зная общую массу атмосферы Q (г) и среднюю молярную массу воздуха Мвозд.(г/моль), определим общее количество условных молей воздуха в атмосфере Nвозл.: Nвозд. = 5 . 1015 . 106/28,96 = 1,7 . 1020 (моль), где 106 – коэффициент перевода тонн в граммы. Поскольку мольные и объемные доли газов в смеси равны между собой, можно найти количество молей кислорода в атмосфере: Nкисл = Nвозд. . aкисл = 1,7 . 1020 . 0,2095 = 3,6 . 1019 (моль) Теперь легко найти массу кислорода в атмосфере: Qкисл = Nкисл . Мкисл =3,6 . 1019 . 32 = 11,5 . 1020 (г) » 12 . 1017 (кг) Ответ:масса кислорода в атмосфере равна 12 . 1017кг.
Пример 8.Во сколько раз количество молекул кислорода в кубическом сантиметре воздуха на высоте вершины Эльбрус (5621 м над уровнем моря) меньше, чем среднее значение у поверхности Земли (на уровне моря) при нормальном атмосферном давлении? Решение.Количество молекул, содержащееся в одном кубическом сантиметре воздуха (nв), можно определить по уравнению: Nв = NAT0P1/(T1P0Vm), где NA – число Авогадро; Vm – молярный объем газа при стандартных условиях (Vm= 22,4 . 103 см3); Т0, Р0 и Т1, Р1– значения температуры (К) и давления при стандартных условиях и в рассматриваемом случае соответственно. Давление у поверхности Земли (на уровне моря) при нормальных условиях равно давлению при стандартных условиях (Р1 = P0). Средняя температура воздуха у поверхности Земли (на уровне моря) равна 288 К (таблица 2). В этом случае количество молекул газов в кубическом сантиметре воздуха составит: nв.3 = 6,02 . 1023 . 273/ (288 . 22,4 . 103) = 2,55 . 1019 (см–3) Количество молекул кислорода в кубическом сантиметре воздуха (nк) можно определить, зная его среднее содержание в воздухе: nк = nвC*к, где C*к– объемная доля кислорода в воздухе. Количество молекул кислорода в кубическом сантиметре воздуха у поверхности Земли (на уровне моря) при нормальном атмосферном давлении, средней температуре уповерхности и концентрации кислорода в приземном слое атмосферы, равной среднему значению, составит: nк.З = nв.ЗС*к где С*к – среднее значение концентрации кислорода в приземном слое воздуха (таблица 1.1), выраженное в объемных долях. nк.3 = 2 . 55 . 1019 . 0,2095 = 5,34 . 1018 (см–3) Содержание молекул воздуха в атмосфере убывает с увеличением высоты над уровнем моря (уравнение 5):
где nв.H – концентрация молекул в воздухе на высоте H, см–3; nв.з – средняя концентрация молекул в воздухе на уровне моря, см–3; М – средняя молярная масса воздуха (М = 28,96 . 10–3 кг/моль – пример 7); g – ускорение силы тяжести (g= 9,8 м/с2); Н – высота над уровнем моря, м; R – универсальная газовая постоянная, Дж/(моль . К); Тн – средняя температура воздуха на высоте Н, К. Температуру на заданной высоте в тропосфере можно оценить по уравнению: ТН = Т3 + DT . H , где Тни Tз – температуры на заданной высоте H и у поверхности Земли соответственно, К; DT–температурныйградиент в стандартной тропосфере (DT = – 6,5К/км – таблица 2). Средняя температура атмосферы на высоте вершины Эльбрус составит: ТН = 288 + (–6,5) . 5,621 = 252 (К) Концентрация молекул воздуха на высоте вершины Эльбрус составит: nв.Н = 2,55 . 1019 ехр[–28,96 . 10-3 . 9,8 . 5621/(8,31 . 252)] = 1,19 . 1019(см–3) Поскольку соотношение чисел молекул «квазипостоянных» компонентов воздуха в единице объема практически не меняется в атмосфере до высоты 100 км, можно определить концентрацию молекул кислорода на высоте вершины Эльбрус (nк.Н) по уравнению: nк.Н = Nв.НС*к nк.Н = 1,19 . 1019 . 0,2095 = 2,49 . 1018 (см–3) Отношение количества молекул кислорода в воздухе у поверхности Земли (на уровне моря) и на вершине горы Эльбрус составит: Х = nк.з/nк.H; X = 5,34 . 1018/(2,49 . 1018) = 2,1. Ответ: концентрация молекул кислорода в воздухе на вершине Эльбрус в 2,1 раза меньше, чем у поверхности Земли. Пример 9.Определите среднее время пребывания паров воды в атмосфере, если по оценкам специалистов в атмосфере находится 12900 км3 воды, а на поверхность суши и океана выпадает в виде атмосферных осадков в среднем 577 . 1012 м3 воды в год. Решение. Среднее время пребывания компонентов в атмосфере в условиях динамического равновесия можно определить из уравнения (1): t = A/Q где t – время пребывания вещества в атмосфере, в единицах времени; А – количество вещества в атмосфере, в единицах массы; Q– скорость поступления или вывода вещества из атмосферы, в единицах массы на единицу времени. Для условий задачи имеем: t = 12900 . 109/(577×1012) = 2,23 . 10–2 года = 8,2 дня, где 109 – коэффициент перевода км3 в м3. Ответ:среднее время пребывания воды в атмосфере составляет 8,2 дня. Пример 10.Количество метана, поступающего ежегодно с поверхности Земли в атмосферу, составляет 550 млн т. Среднее содержание метана в слое атмосферы, на который приходится 90% ее массы, составляет 1,7 млн–1. Определите время пребывания метана в этом слое атмосферы, если принять, что в других частях атмосферы он отсутствует. Решение. Оцененное нами ранее (пример 7) количество молей воздуха в атмосфере равно 1,7 . 1020. В слое, составляющем 90% массы атмосферы, будет содержаться воздуха Nвозд. = 1,7 . 1020 . 90/100 = 1,53 . 1020 (моль) Количество молей метана, содержащегося в этом слое атмосферы, составит: N мет =N возд.С*мет , где С*мет – объемная доля метана в воздухе, по условию задачи. С*мет = 1,7млн–1 = 1,7 × 10–6; Nмет = 1,53 × 1020 × 1,7 × 10-6 = 2,6 × 1014 (моль) Масса метана в рассматриваемом слое атмосферы составит: Aмет = Nмет×Ммет где Ммет – молярная масса метана (16 г/моль); Амет = 2,6 × 1014 × 16 = 41,6 × 1014 (г) = 41,6 × 108 (т) Время пребывания метана в атмосфере составит (Пример.9): t = А/Q По условию задачи, Q = 500 млн т/год. Тогда t = 41,6 × 108/(550×106) = 7,6 (года) Ответ: время пребывания метана в слое, содержащем 90% массы атмосферы, составляет 7,6 года.
Пример 11. Определите среднеквадратичную скорость движения молекул азота в приземном слое воздуха. Решение. Среднеквадратичную скорость движения молекул идеального газа можно определить по уравнению:
где R – универсальная газовая постоянная [R = 8,314 Дж/(моль × К)]; Т – температура газа, К; М – молярная масса газа, кг/моль. Средняя температура воздуха у поверхности Земли соответствует температуре нижней границы тропосферы. Для стандартной атмосферы эта температура равна 15°С (таблица 2). Для этого слоя воздуха, если принять, что он является идеальным газом, среднеквадратичная скорость движения молекул азота (N2) составит:
Ответ: среднеквадратичная скорость движения молекул азота в приземном слое воздуха при температуре 15°С составит 500 м/с. Пример 12. Среднеквадратичная скорость движ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Физико-химические процессы в атмосфере: Учебное пособие. – Саратов: СВИРХБЗ, 2006. – 103 с.
Физико-химические процессы в атмосфере: Учебное пособие. – Саратов: СВИРХБЗ, 2006. – 103 с.



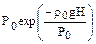 , (3)
, (3)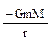 , (7)
, (7)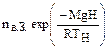 ,
,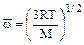 ,
, – среднеквадратичная скорость молекул газа, м/с;
– среднеквадратичная скорость молекул газа, м/с;