
|
|
Производная функции, заданной параметрическиЧасто применяется способ задания функции, при котором текущие координаты являются функцией третьей переменной величины, параметра t:
Пример: x/t = 2а sint×cost; y/t = -3а cos2t×sint, тогда у/ =
Лекция № 7 Дифференциал функции Понятие дифференциала Пусть функция Где Обозначается:
Дифференциал dy называется также дифференциалом первого порядка . Найдем дифференциал независимой переменной х, т.е. дифференциал функции y=x. Так как Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной . Теорема Если функция имеет дифференциал в точке Доказательство: 1) Пусть функция y=f(x) дифференцируема в точке х, т.е.
Обратно: 2)Пусть функция y=f(x) имеет производную в точке х, т.е.
Геометрический смысл дифференциала
Для этого проведём к графику функции y=f(x) в точке M(x;y) касательную MT и рассмотрим ординату этой касательной для точки
Но, согласно геометрическому смыслу производной, Сравнивая полученный результат с формулой Приложение дифференциала к приближенным вычислениям Т.к. То
Используя это равенство можно оценивать приближенное значение функции вблизи точек, в которых известно точное значение функций. Свойства дифференциала функции Производная как отношение дифференциалов. Пусть 1. 2. 3. 4. 5. Дифференциал сложной функции Теорема: Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента (если обе функции дифференцируемы) Доказательство:
По правилу диф. сложной функции:
Таблица дифференциалов
Производные и дифференциалы высших порядков Определение. Второй производной, или производной второго порядка, называется производная от первой производной. Обозначается
Определение. Дифференциалом второго порядка называется дифференциал от первого дифференциала.
Замечание: Дифференциалы высших порядков свойством инвариантности не обладают.
Лекция №8 Теоремы о дифференцируемых функциях Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение Теорема Ролля. Если функция f(x) непрерывна на отрезке Доказательство. Так как функция f(x) непрерывна на отрезке Если m=M, то функция f(x) постоянна на Если Пусть, например, функция принимает значение M в точке
Найдём производную
В силу условия Если, Таким образом, В случае, когда f(c)=m, доказательство аналогичное. Ч.т.д. Геометрически теорема Ролля означает, что на графике функции y=f(x) найдётся точка, в которой касательная к графику параллельна оси Ox (см. рис.1 и 2). На рис. 3 таких точек две. Теорема Коши Если функции f(x) и j(x)непрерывны на отрезке
Доказательство. Отметим, что
Она удовлетворяет всем условиям теоремы Ролля: непрерывна на отрезке На основании теоремы Ролля найдётся точка
Отсюда следует
Теорема Лагранжа Если функция f(x) непрерывна на отрезке
Доказательство. Теорему Лагранжа можно рассматривать как частный случай теоремы Коши. Действительно, положив j(x)= x, находим Подставляя эти значения в формулу Замечание: Полученную формулу
Называют формулой Лагранжа или формулой о конечном приращении: Приращение дифференцируемой функции на отрезке [a,b] равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка Следствие 1 :Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке. Следствие 2: Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое. Правило Лопиталя Данное правило помогает раскрыть неопределенности вида Правило Лопиталя раскрытия неопределённостей вида Пусть функции f(x) и j(x) непрерывны и дифференцируемы в окрестности точки x0 и обращаются в нуль в этой точке: f(x0) = j(x0) = 0. Пусть
Учитывая, что f(x0) = j(x0) = 0, получаем
При
Так как Ч.т.д. 8.5. Правило Лопиталя для раскрытия неопределенности вида Пусть f(x) и g(х) – функции, непрерывны и дифференцируемы в некоторой окрестности точки х0, за исключением быть может самой точки х0, и при х®х0 обе эти функции стремятся к бесконечности. Тогда если существует предел
Замечания: 1) теорема остается справедливой и в том случае, если х ® ±¥ или х®х0±0; 2) если Примеры: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , такой способ задания называется параметрическим.
, такой способ задания называется параметрическим. перейдем к пределу:
перейдем к пределу: 

 Получаем:
Получаем: .
. Найти у/.
Найти у/. = -1,5cost.
= -1,5cost. имеет в точке х отличную от нуля производную
имеет в точке х отличную от нуля производную  . Тогда по теореме о связи функции, ее предела и бесконечно малой функции, приращение функции можно записать:>
. Тогда по теореме о связи функции, ее предела и бесконечно малой функции, приращение функции можно записать:> 


 - постоянная, не зависящая от
- постоянная, не зависящая от  ,
,  - б.м. более высокого порядка малости, чем
- б.м. более высокого порядка малости, чем 
 . Дифференциалом функции y=f(x) в точке
. Дифференциалом функции y=f(x) в точке  называется главная часть приращения функции, линейная относительно
называется главная часть приращения функции, линейная относительно  , или
, или

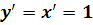 , то
, то  , т.е. дифференциал независимой переменной равен приращению этой переменной. Поэтому
, т.е. дифференциал независимой переменной равен приращению этой переменной. Поэтому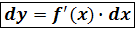
 , то функция имеет производную в этой точке и обратно.
, то функция имеет производную в этой точке и обратно. разделив это равенство на
разделив это равенство на 
 и взяв предел при
и взяв предел при  получим:
получим: т.е. функция имеет производную в точке х.
т.е. функция имеет производную в точке х. ,
,  - б.м. при
- б.м. при 
 , где
, где  - б.м. более высокого порядка, т.е. функция имеет дифференциал в точке х.
- б.м. более высокого порядка, т.е. функция имеет дифференциал в точке х.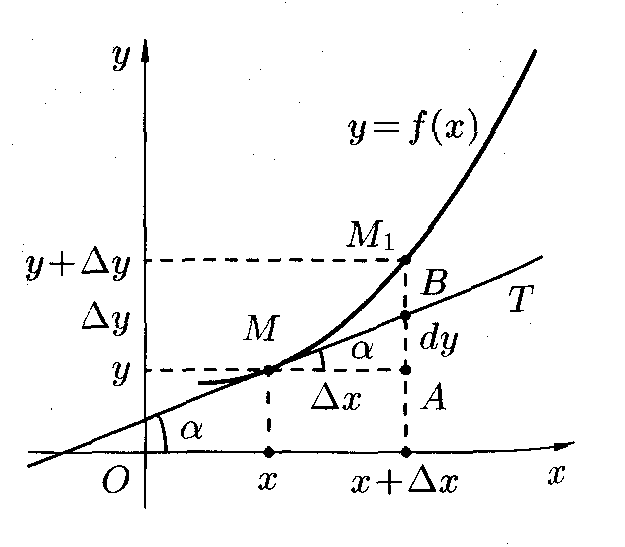 Выясним геометрический смысл дифференциала.
Выясним геометрический смысл дифференциала. (см. рис.). На рисунке
(см. рис.). На рисунке  Из прямоугольного треугольника MAB имеем:
Из прямоугольного треугольника MAB имеем: т.е.
т.е. 
 Поэтому
Поэтому 
 получаем
получаем  т. е. дифференциал функции y=f(x) в точке x равен приращению ординаты касательной графику функции в этой точке, когда x получит приращение
т. е. дифференциал функции y=f(x) в точке x равен приращению ординаты касательной графику функции в этой точке, когда x получит приращение  .
. , где
, где  - б.м.
- б.м.


 , тогда
, тогда 
 , тогда
, тогда 
 , т.е. производная равна отношению дифференциалов.
, т.е. производная равна отношению дифференциалов.

 , тогда
, тогда 
 ,
, 

 , пусть
, пусть  ,
, 
 . Умножим на
. Умножим на  обе части:
обе части: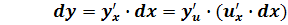
 Замечание: здесь
Замечание: здесь  - функция, а
- функция, а 



 , если y=f(x)
, если y=f(x)
 если
если 

 , n≠-1
, n≠-1














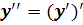 . Для обозначения второй производной используются символы:
. Для обозначения второй производной используются символы:
 , т.к.
, т.к.  , то
, то  - постоянная по отношению к
- постоянная по отношению к  , т.е.
, т.е.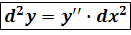
 , дифференцируема на интервале
, дифференцируема на интервале  и на концах отрезка принимает одинаковые значения f(a)= f(b), то найдётся, хотя бы одна точка
и на концах отрезка принимает одинаковые значения f(a)= f(b), то найдётся, хотя бы одна точка  , в которой производная
, в которой производная  обращается в нуль, т.е.
обращается в нуль, т.е. 
 в любой точке отрезка
в любой точке отрезка  , то функция достигает, хотя бы одно из значений M или m во внутренней точке с интервала
, то функция достигает, хотя бы одно из значений M или m во внутренней точке с интервала  , т. е. f(c)=M. Тогда для всех
, т. е. f(c)=M. Тогда для всех  выполняется соотношение
выполняется соотношение


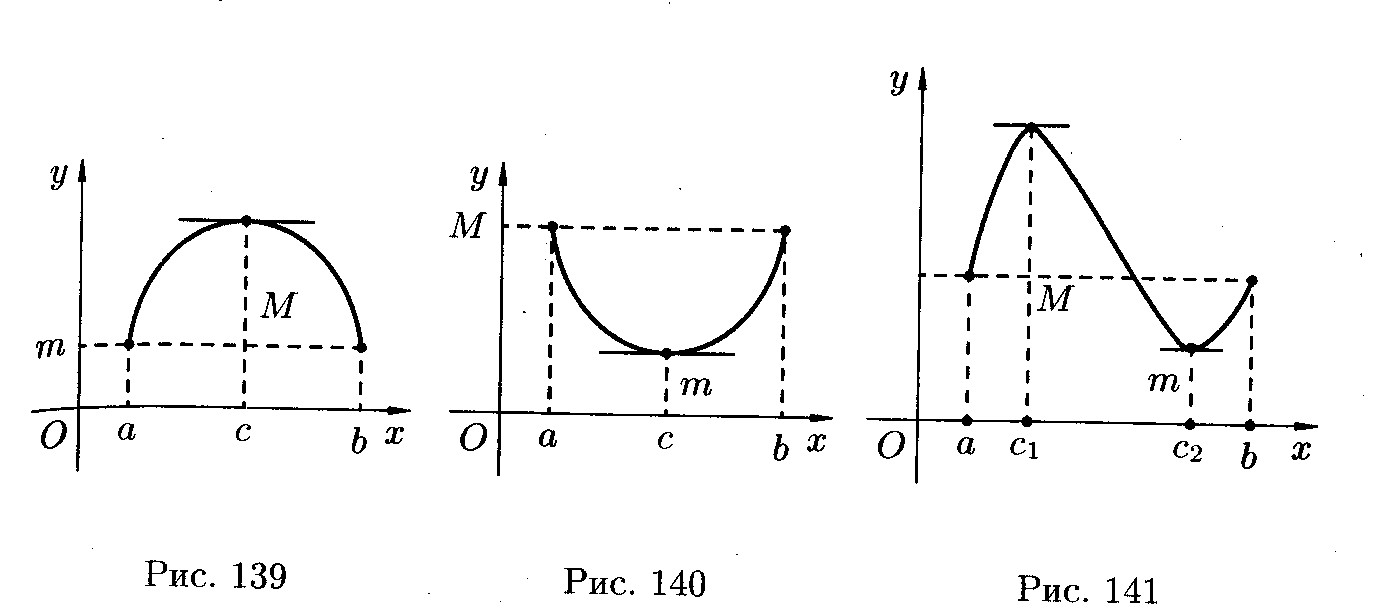
 . Если
. Если  (т. е.
(т. е.  справа от точки x=c), то
справа от точки x=c), то  и поэтому
и поэтому 
 то
то  и
и 
 для
для  , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  такая, что выполняется равенство
такая, что выполняется равенство .
. , т. к. в противном случае по теореме Ролля нашлась бы точка c, такая, что
, т. к. в противном случае по теореме Ролля нашлась бы точка c, такая, что  , чего не может быть по условию теоремы. Рассмотрим вспомогательную функцию
, чего не может быть по условию теоремы. Рассмотрим вспомогательную функцию .
. .
. . Но
. Но  , следовательно,
, следовательно,
 и
и  Ч.т.д.
Ч.т.д.

 или
или  и
и  при вычислении пределов.
при вычислении пределов.
 в окрестности точки x0. Если существует предел
в окрестности точки x0. Если существует предел  , то
, то
 Доказательство. Возьмем точку х, принадлежащую окрестности точки x0 Применим к функциям f(x) и j(x) теорему Коши на отрезке [x0;x]. Тогда
Доказательство. Возьмем точку х, принадлежащую окрестности точки x0 Применим к функциям f(x) и j(x) теорему Коши на отрезке [x0;x]. Тогда  где с лежит между x0 и x (см. рис.).
где с лежит между x0 и x (см. рис.).
 величина с также стремится к x0; перейдём к пределу:
величина с также стремится к x0; перейдём к пределу:

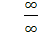
 при х®х0, то существует и предел отношения самих функций, причем, они равны, т.е.
при х®х0, то существует и предел отношения самих функций, причем, они равны, т.е. =
=  .
.