
|
|
Функция, имеющая производную в каждой точке интервала, называется дифференцируемой на этом интервале. Операция нахождения производной функции называется дифференцированием.Определение: Закон, по которому каждой точке Для обозначения производной функции применяются следующие обозначения: Связь между непрерывностью и дифференцируемостью
Теорема : Если функция дифференцируема в некоторой точке, то она непрерывна в ней. Доказательство: Пусть функция y=f(x) дифференцируема в некоторой точке x. Следовательно, существует предел Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, имеем: Переходя к пределу, при Обратная теорема неверна: непрерывная функция может не иметь производной. Примером такой функции является функция
Изображённая на рисунке функция не прерывна в точке x=0, но не дифференцируема в ней. Геометрический смысл производной
Рассмотрим график непрерывной функции y=f(x). Пусть в точке При
Если функция y=f(x) имеет невертикальную касательную в точке Справедливо и обратное утверждение: Если функция Уравнение касательной к графику функции в точке с абсциссой Нормаль-это прямая, проходящая через точку касания и перпендикулярная касательной. Уравнение нормали: Пример: Составить уравнения касательной и нормали к графику кривой у = 2 Решение: 1. у/ = 2. у/(х0) = у/( 3. у(х0) = у( 4. Тогда уравнения касательной и нормали имеют вид: у - у -
Основные правила дифференцирования
1. Производная постоянной величины равна Доказательство: Дадим приращение
Производная суммы двух функций равна сумме производных.
Доказательство:
3. Производная произведения двух функций: Пример: Найти производную функции: у = соsx×ln2x. y/ = (cosx)/ ln2x + cosx (ln2x)/ = - sinx ln2x + cosx×2lnx×(lnx)/ = - sinx×ln2x +cosx×2lnx×( 4. Производная частного: Если
Пример: Найти производную функции: y = y/ = 5. Производная сложной функции: Если Доказательство: Дадим По условию
Правила дифференцирования: 1. С/ = 0 2. (CU)/ = CU 3. (U±V)/ = U/ ± V/ 4. (UV)/ = U/V + UV/ 5. Таблица производных
Производная обратной функции Если
Доказательство:
Производная неявно заданной функции Если функция задана неявно Производная показательно- степенной функции Пусть Прологарифмируем обе части:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ставится в соответствие производная в этой точке, называется производной функции на множестве (a,b).
ставится в соответствие производная в этой точке, называется производной функции на множестве (a,b).


 где
где  при
при  т.е.
т.е. 
 А это и означает, что функция y=f(x) непрерывна в точке x, ч.т.д.
А это и означает, что функция y=f(x) непрерывна в точке x, ч.т.д.

 Касательной к данной кривой в данной точке М называется предельное положение МТ секущей MN, проходящей через точку М, когда вторая точка секущей N, неограниченно приближается по кривой к точке М.
Касательной к данной кривой в данной точке М называется предельное положение МТ секущей MN, проходящей через точку М, когда вторая точка секущей N, неограниченно приближается по кривой к точке М. функция имеет невертикальную касательную (предельное положение секущей). Найдем угловой коэффициент секущей k=tg
функция имеет невертикальную касательную (предельное положение секущей). Найдем угловой коэффициент секущей k=tg  , где
, где 
 стремящемся к нулю,
стремящемся к нулю, 
 .
. - угловой коэффициент касательной.
- угловой коэффициент касательной. , равная тангенсу угла наклона касательной к графику функции в точке
, равная тангенсу угла наклона касательной к графику функции в точке  .
. имеет производную в точке
имеет производную в точке  .
. .
. в точке с абсциссой х0 =
в точке с абсциссой х0 =  .
. ((3-х2)/2)/ =
((3-х2)/2)/ =  = -
= -  .
. = - 2(х -
= - 2(х -  (х -
(х -  .
. ,
,  .
.
 .
. .
. , если
, если  и
и  - дифференцируемые функции, то их алгебраическая сумма дифференцируема.
- дифференцируемые функции, то их алгебраическая сумма дифференцируема. .
. По определению производной:
По определению производной: .
. .
. ).
). , то
, то


 и
и  - дифференцируемые функции от своих аргументов, то производная сложной функции
- дифференцируемые функции от своих аргументов, то производная сложной функции  существует и равна
существует и равна  .
. , тогда
, тогда  ,
,  .
.

 .
. . Перейдем к пределу
. Перейдем к пределу



 - дифференцируема,
- дифференцируема,  непрерывна в точке
непрерывна в точке 


 .
. при V¹0.
при V¹0.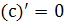
 Un-1
Un-1 







 дифференцируемая функция с отличной от нуля производной, то производная обратной функции
дифференцируемая функция с отличной от нуля производной, то производная обратной функции  равна обратной величине производной данной функции:
равна обратной величине производной данной функции:
 - соответствующее приращение обратной функции
- соответствующее приращение обратной функции 

 при
при  )
) .
. , следует продифференцировать обе части тождества, применяя правило дифференцирования сложной функции (помня, что
, следует продифференцировать обе части тождества, применяя правило дифференцирования сложной функции (помня, что  - функция от
- функция от  ).
). ,
, 





 .
.