
|
|
Основные элементарные функции и их области определенияЛекция № 1 Функция, ее свойства , способы задания 1.1. Некоторые простейшие логические символы:
: - «имеет место»; Числовые промежутки, окрестность точки Напомним, что между точками числовой оси и множествам 1) интервал 2) отрезок (сегмент) 3) полуинтервал, закрытый слева 4) полуинтервал, закрытый справа Эти множества будем обозначать 5) полуось, Любой интервал, содержащий точку Часто рассматривают окрестности, симметричные относительно Опр: Интервал вида Если из этого интервала выколоть точку 1.3. Функции, способы задания, свойства
Изучая явления, мы обычно имеем дело с совокупностью переменных величин, которые связаны между собой так, что значения одних величин (независимые переменные) полностью определяют значения других (зависимые переменные или функции). Определение: Переменная величина y называется функцией (однозначной) от переменной x, если они связаны между собой так, что каждому значению величины x из некоторого множества Область определения функции f обозначается D(f), множество значений: E(f). Способы задания функции: Табличный, когда значения аргумента и соответствующие значения функции заданы таблицей. 2.Графический, когда соответствие аргумента и функции даны в виде графика; Аналитический, когда зависимость дана в виде формулы. 1.4. Основные свойства функции: Определение: Функция у=f(х) называется четной, если для любого значения х и –х, взятых из области определения функции, выполняется равенство f(-x)=f(x). Из определения следует, что график четной функции симметричен относительно оси ординат(Оу). Примеры четных функций: y= Определение: Функция у=f(х) называется нечетной, если для любого значения х и –х, взятых из области определения функции, выполняется равенство f(-x)= -f(x). Из определения следует, что график нечетной функции симметричен относительно начала координат. Примеры нечетных функций: y= Определение: Функция у=f(х) называется периодической, если существует такое число Т>0, что f(x+T)=f(x) для всех х Определение: Функция у=f(x) называется возрастающей на промежутке (а; b), если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее значение функции. Т.е. если для любых
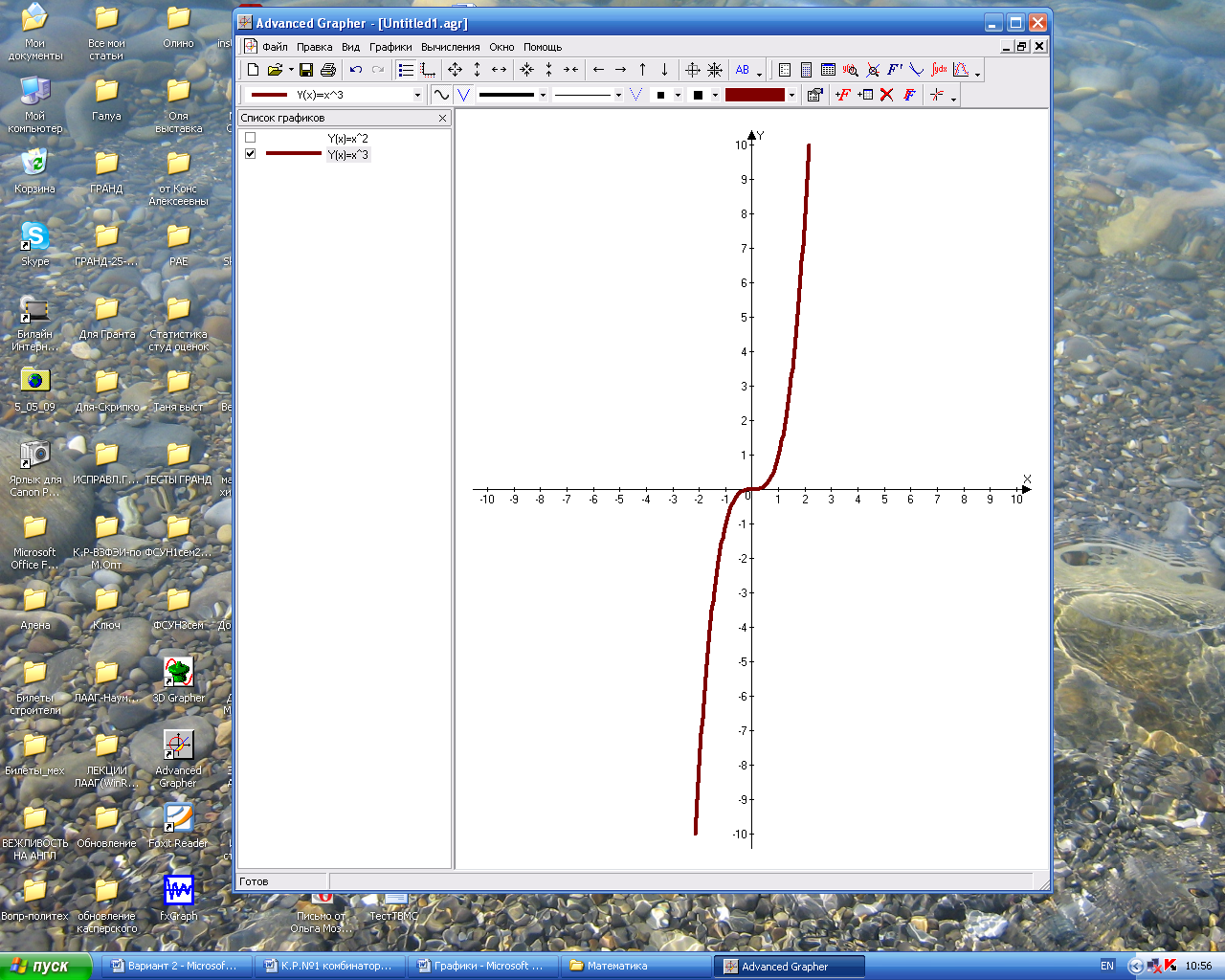
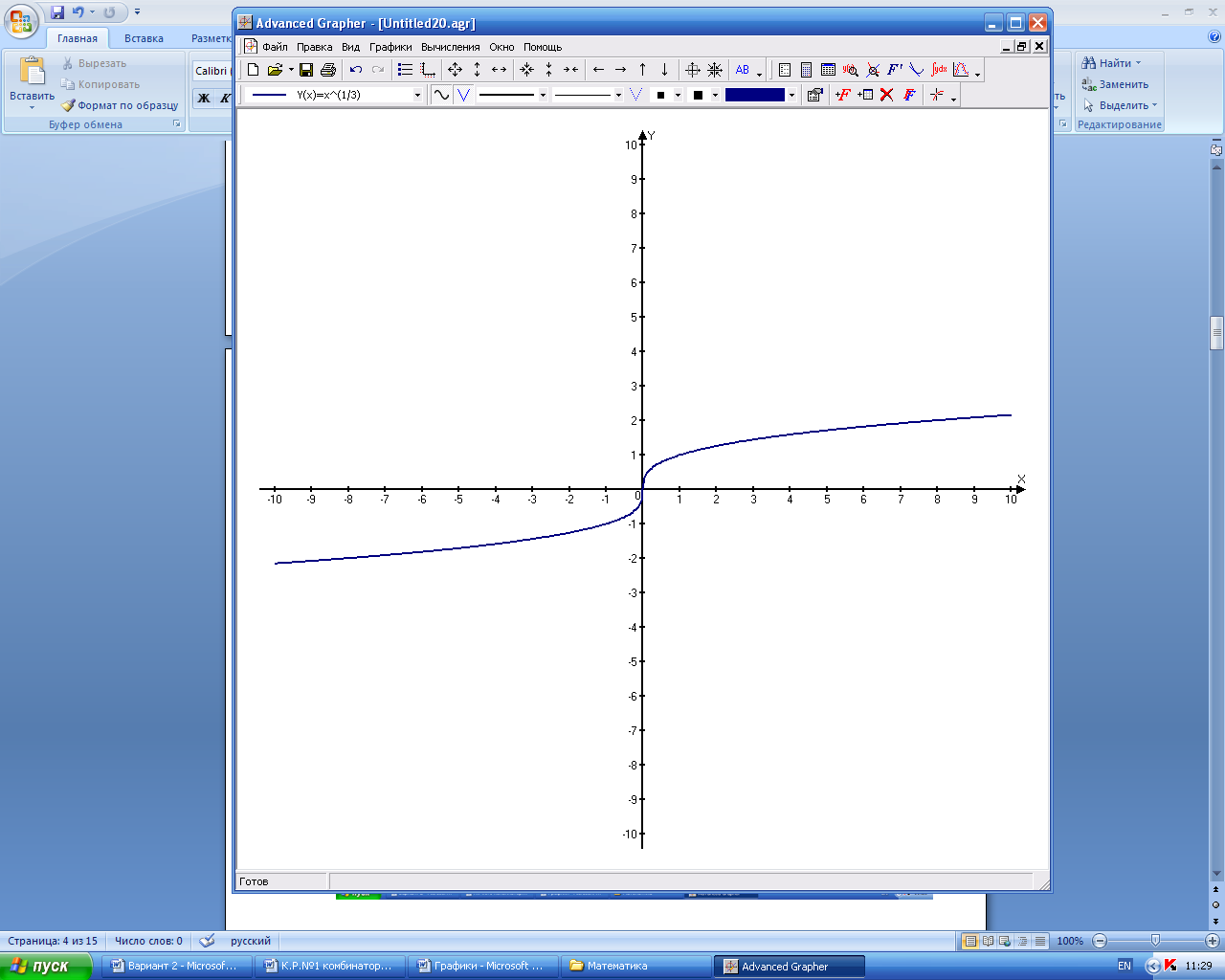
Определение: Функция у=f(x) называется убывающей на промежутке (а; b), если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует меньшее значение функции. Т.е. если из Основные элементарные функции и их области определения 1. Функция 2. Степенная функция у=хn с рациональным положительным показателем
3. Показательная функция,
4. Логарифмическая функция у=
5. Тригонометрические функции y=sinx , y=cosx определены на всей числовой оси; y=sinx y=cosx
y=tgx определена на всей числовой оси, исключая точки х= у=ctgx определена на всей числовой оси, исключая точки х=
6. Обратные тригонометрические функции y=arccosx и y=arcsinx определены на отрезке [-1;1] ; y=arctgx и y=arcctgx определены на всей числовой оси.
Сложная функция Пусть задана функция Например: Обратная функция Пусть задана функция y=f(x) c областью определения D(f), множеством значений E(f). Если каждому значению 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – означает «из предложения
– означает «из предложения  следует предложение
следует предложение  »;
»; – «предложения
– «предложения  равносильны», т.е. из
равносильны», т.е. из 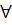 - означает «для любого», «для всякого»;
- означает «для любого», «для всякого»; - «существует», «найдется»;
- «существует», «найдется»; - действительных чисел, существует взаимно- однозначное соответствие, поэтому вместо слова «число» часто говорят «точка», а подмножества действительных чисел называют числовыми промежутками, или интервалами. Наиболее часто эти множества представляют собой:
- действительных чисел, существует взаимно- однозначное соответствие, поэтому вместо слова «число» часто говорят «точка», а подмножества действительных чисел называют числовыми промежутками, или интервалами. Наиболее часто эти множества представляют собой: , т.е.
, т.е. 
 , т.е.
, т.е. 
 ,
, 

 и называть промежутками.
и называть промежутками. ;
; , называется окрестностью точки
, называется окрестностью точки  .
. называется
называется  - окрестностью точки
- окрестностью точки  , то выполняется неравенство
, то выполняется неравенство  , или, что то же самое
, или, что то же самое  . Обозначается
. Обозначается  соответствует единственное вполне определенное значение величины y из множества
соответствует единственное вполне определенное значение величины y из множества  . Записывается этот факт :
. Записывается этот факт : 
 , y=cos(x), y=x
, y=cos(x), y=x  sin(x), y=ln
sin(x), y=ln  ,
,  и т.д.
и т.д. , y=sin(x), y=x
, y=sin(x), y=x  и т.д.
и т.д. D(f). Наименьшее число Т, если такое существует, называется периодом функции.
D(f). Наименьшее число Т, если такое существует, называется периодом функции.
 (а;b), из условия
(а;b), из условия .
. .
. определена на общей области определения функций f(x) и g(x), при условии, что g(x)≠0.
определена на общей области определения функций f(x) и g(x), при условии, что g(x)≠0. при нечетном
при нечетном  определена на всей числовой оси, а при четном определена на интервале
определена на всей числовой оси, а при четном определена на интервале 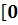 ;∞), (т.е. для функции
;∞), (т.е. для функции  , f(x)≥0).
, f(x)≥0).





 , a>0, a≠1, определена на всей числовой оси. При a>1 функция возрастающая, при а<1 функция убывающая.
, a>0, a≠1, определена на всей числовой оси. При a>1 функция возрастающая, при а<1 функция убывающая.

 , а>0, а≠1, определена на интервале (0;∞). При a>1 функция возрастающая, при а<1 функция убывающая.
, а>0, а≠1, определена на интервале (0;∞). При a>1 функция возрастающая, при а<1 функция убывающая.


 ;
; .
.

 c множеством определения
c множеством определения  и множеством значений
и множеством значений  , и функция y=f(u), областью определения которой является
, и функция y=f(u), областью определения которой является  . Переменная
. Переменная 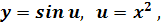
 - синус квадрата.
- синус квадрата. соответствует единственное значение
соответствует единственное значение  , то определена обратная функция
, то определена обратная функция  (которая иногда обозначается
(которая иногда обозначается  ) с областью определения E и множеством значений D. Про такие функции y=f(x) и
) с областью определения E и множеством значений D. Про такие функции y=f(x) и