
|
|
Решение. По правилу нахождения предела многочлена находим
Пример 2: Вычислить Решение. Так как при
Пример 3: Вычислить Решение. Предел делителя равен нулю: Так как Пример 4: Вычислить Решение. Здесь пределы числителя и знаменателя при Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и следовательно, сделать возможным применение теоремы III. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо, По определению предела функции аргумент х стремится к своему предельному значению, никогда не принимая этого значения; поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем:
Пример 5: Вычислить Решение. Пределы числителя и знаменателя при Разложим квадратный трёхчлен в числителе на линейные множители по формуле
Пример 6: Вычислить Решение. Пределы числителя и знаменателя при Разложив числитель и знаменатель на множители и сократив затем на
Пример 7: Вычислить Решение. Очевидно, что при
Пример 8: Вычислить Решение. Вынося
(при Пример 9: Вычислить Решение. При Пример 10: Вычислить Решение. При
(при Пример 11: Вычислить Решение. Разделим числитель и знаменатель на наивысшую степень аргумента в знаменателе, т.е. на
После сокращения в числители величина ограниченная, в знаменателе величина бесконечно малая, следовательно, пределом является величина бесконечно большая.
Пример 12: Вычислить Решение. При
Лекция № 4 Первый и второй замечательные пределы Теорема (первый замечательный предел)
Предел отношения синуса бесконечно малой дуги к длине дуги равен единице. Доказательство: Возьмем круг радиуса 1. Обозначим радианную меру угла АОС через х.
Т.к. 2) пусть Замечание1: Замечание 2: Замечание 3: Покажем это:
Примеры Вычислить следующие пределы: 1. Решение. Очевидно, что при x→π/2 числитель и знаменатель дроби стремиться к нулю. Разложив числитель и знаменатель на множители и сократив дробь на
2. Решение. Преобразуя заданное выражение и используя первый замечательный предел, получим
3. Решение. Имеем 4. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
. знаменатель дроби отличен от нуля, то по правилу нахождения предела дробно-рациональной функции получим
знаменатель дроби отличен от нуля, то по правилу нахождения предела дробно-рациональной функции получим
 .
. Следовательно, теорему о пределе применять нельзя.
Следовательно, теорему о пределе применять нельзя. то
то  при
при  есть бесконечно малая, а обратная ей величина
есть бесконечно малая, а обратная ей величина  — бесконечно большая. Поэтому при
— бесконечно большая. Поэтому при  произведение
произведение  есть величина бесконечно большая, т.е.
есть величина бесконечно большая, т.е. 

 равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, так как при
равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, так как при  получается отношение двух бесконечно малых величин.
получается отношение двух бесконечно малых величин.
 .
. равны нулю:
равны нулю: 

 где
где  и
и  — корни трёхчлена. Разложив на множители и знаменатель, сократим дробь на
— корни трёхчлена. Разложив на множители и знаменатель, сократим дробь на  . Используя следствие 4, получим
. Используя следствие 4, получим

 , равны нулю:
, равны нулю: 
 получим
получим


 функция представляет собой разность двух бесконечно больших величин. Выполнив вычитание дробей, получим дробь, числитель и знаменатель которой при
функция представляет собой разность двух бесконечно больших величин. Выполнив вычитание дробей, получим дробь, числитель и знаменатель которой при  стремятся к нулю. Сократив дробь на
стремятся к нулю. Сократив дробь на  , получим
, получим
 .
. за скобки, получим
за скобки, получим
 величины
величины  — бесконечно малые и их пределы равны нулю).
— бесконечно малые и их пределы равны нулю).
 знаменатель
знаменатель  неограниченно растёт, т.е. является величиной бесконечно большой, а обратная величина
неограниченно растёт, т.е. является величиной бесконечно большой, а обратная величина  – бесконечно малой. Произведение
– бесконечно малой. Произведение  бесконечно малой на ограниченную величину (постоянная—частный случай ограниченной величины) есть величина бесконечно малая, и предел её при
бесконечно малой на ограниченную величину (постоянная—частный случай ограниченной величины) есть величина бесконечно малая, и предел её при  равен нулю. Следовательно,
равен нулю. Следовательно, 

 числитель и знаменатель—величины бесконечно большие. Поэтому при непосредственном применении теоремы III получаем выражение
числитель и знаменатель—величины бесконечно большие. Поэтому при непосредственном применении теоремы III получаем выражение  которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель разделить на
которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель разделить на  :
:
 — величины бесконечно малые и, следовательно, их пределы равны нулю).
— величины бесконечно малые и, следовательно, их пределы равны нулю).
 :
:

 .
. данная функция представляет собой разность двух бесконечно больших величин
данная функция представляет собой разность двух бесконечно больших величин  . Умножив и разделив функцию на выражение
. Умножив и разделив функцию на выражение  получим
получим

 Рассмотрим: 1)Пусть
Рассмотрим: 1)Пусть  ; можно считать, что
; можно считать, что  , т.к.
, т.к.  ;
;  ;
;
 , площадь сектора
, площадь сектора 
 разделим это неравенство на 1/2sinx>0
разделим это неравенство на 1/2sinx>0
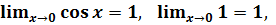 то по теореме о 2-х милиционерах
то по теореме о 2-х милиционерах 
 , тогда
, тогда 
 при
при  .
.
 действительно, при
действительно, при 

 , тогда получим
, тогда получим , но так как
, но так как  , то
, то  .
. .
. получим
получим




