
|
|
Все точки разрыва разделяются на точки разрыва первого и второго рода.Определение: Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. При этом: 1) если А1=А2 , и f(x) 2) если Точка разрыва х0 называется точкой разрыва второго рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности. Пример1: Исследовать функцию Решение:
Предел слева:
Предел справа:
В точке х=2 функция имеет разрыв второго рода.
Пример2: Дана функция Решение:
Очевидно, что
Основные теоремы о непрерывных функциях Теорема 1: Сумма, произведение и частное двух непрерывных функций есть функция непрерывная(для частного за исключением тех значений аргумента, в которых делитель равен нулю) Теорема 2: Если функция непрерывна в точке Теорема 3: Если функция y=f(x) непрерывна и строго монотонна на отрезкеr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Замечание 1: Все основные элементарные функции непрерывны при всех значениях переменной х, при которых они определены. Замечание 2: Функция, полученная из элементарных с помощью конечного числа арифметических действий и суперпозиций (операция взятия функции от функции) непрерывна при тех значениях аргумента, при которых она определена. Свойства функций, непрерывных на отрезке Теорема 1(Вейерштрасса): Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Изображенная на рисунке функция принимает свое наибольшее значение М в точке Теорема 2( Больцано- Коши): Если функция y=f(x) непрерывна на отрезке Следствие: Если функция y=f(x) непрерывна на отрезке
Данное утверждение лежит в основе метода «половинного деления», который используется для нахождения корня уравнения f(x)=0. Метод половинного деления: Для решения уравнения f(x)=0 с заданной точностью 1. Подобрать отрезок 2. Вычислить 3. Если f(x)=0, то х- корень уравнения 4. Если 5. Если
Лекция № 6 ПРОИЗВОДНАЯ ФУНКЦИИ Понятие производной Задача, приводящая к понятию производной: Пусть материальная точка движется по закону Понятие производной Пусть функция y=f(x) определена в некоторой окрестности точки Отношение Определение: Если существует конечный предел отношения приращения функции к приращению аргумента при
Для обозначения производной в точке применяются следующие обозначения: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  .
. , то точка х0 называется точкой устранимого разрыва;
, то точка х0 называется точкой устранимого разрыва; , то х0 называется точкой конечного разрыва, а величину
, то х0 называется точкой конечного разрыва, а величину  называют скачком функции.
называют скачком функции.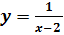 на непрерывность в точке х=2.
на непрерывность в точке х=2. В точке х=2 функция не определена.
В точке х=2 функция не определена.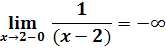
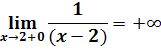
 . Найти точки разрыва, определить их тип.
. Найти точки разрыва, определить их тип. Функция f(x)определена и непрерывна на всей числовой оси, кроме точки х=3.
Функция f(x)определена и непрерывна на всей числовой оси, кроме точки х=3. , следовательно
, следовательно  ,
,  . Поэтому в точке х=3 функция имеет разрыв первого рода. Скачок функции в этой точке равен 1-(-1)=2
. Поэтому в точке х=3 функция имеет разрыв первого рода. Скачок функции в этой точке равен 1-(-1)=2 непрерывна в точке
непрерывна в точке 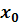 , а функция y=f(u) непрерывна в точке
, а функция y=f(u) непрерывна в точке  Тогда сложная функция
Тогда сложная функция 
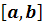 оси ОХ, то обратная ей функция
оси ОХ, то обратная ей функция  также монотонна и непрерывна на соответствующем отрезке
также монотонна и непрерывна на соответствующем отрезке  оси ОУ.
оси ОУ.
 , а наименьшее значение m в точке
, а наименьшее значение m в точке  . Для любого значения
. Для любого значения  имеет место неравенство:
имеет место неравенство:  .
. и принимает на его концах неравные значения f(a)=A, и f(b)=B, то на этом отрезке
и принимает на его концах неравные значения f(a)=A, и f(b)=B, то на этом отрезке 
 , необходимо :
, необходимо : f(b)<0.
f(b)<0.
 , то если f(a)
, то если f(a)  , то b=x , иначе a=x
, то b=x , иначе a=x , то х найден, иначе идти на пункт 2.
, то х найден, иначе идти на пункт 2. . Пусть
. Пусть  - путь, пройденный точкой к моменту времени
- путь, пройденный точкой к моменту времени  . За время
. За время  материальная точка прошла путь
материальная точка прошла путь  . Тогда средняя скорость точки за время
. Тогда средняя скорость точки за время  равна
равна  . При
. При  получим мгновенную скорость точки в момент
получим мгновенную скорость точки в момент  .
. . Дадим аргументу
. Дадим аргументу  , тогда функция получит приращение
, тогда функция получит приращение 
 .
. показывает среднюю скорость изменения функции
показывает среднюю скорость изменения функции  относительно аргумента
относительно аргумента  на промежутке
на промежутке  .
. , то этот предел называется производной функции в точке
, то этот предел называется производной функции в точке 

