
|
|
Строго монотонная функция имеет обратную, причем если сама функция возрастает ( убывает), то и обратная так же возрастает( убывает).Графики функций y=f(x) и Пример: Графики двух взаимно- обратных функций
Неявная функция Функция называется явной, если она задана формулой Функция называется неявной, если она задана уравнением Пример неявно заданной функции: Примеры: 1. Найти область определения функции: 2. Найти множество значений функции: 3. Писать четные функции из данных: 4. Выписать периодические функции: 5. Даны две функции: 6. Найти обратную функцию для данной: Ответы: 1. (D(f)=( 2. (E(f)= 3. 4. ( 5. (f(g(x))= 6. ( Лекция № 2 Последовательность. Предел числовой последовательности Бесконечная числовая последовательность
Опредедение.1 Бесконечной числовой последовательностью называется числовая функция, определенная на множестве N натуральных чисел. Опредедение.2 Последовательность Опредедение.3 Последовательность Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными. Опредедение.4 Последовательность Опредедение.5 Последовательность Опредедение.6 Последовательность Обычно последовательность задается формулой, выражающей общий член последовательности через n. Иногда указывается правило, по которому можно вычислить n-й член последовательности по ее известным предыдущим членам, такой способ задания последовательности называется индуктивным (или рекуррентным). Примеры 1. Вычислить пять первых членов последовательности Решение. Подставив вместо n последовательно 1, 2, 3, 4, 5, получим Написать общий член последовательности натуральных чисел, каждое из которых при делении на 3 дает остаток, равный 1. Решение. Для того чтобы число при делении на-3 давало остаток 1, оно должно иметь вид 3n+1; следовательно, общий член последовательности 3. Последовательность задана рекуррентным соотношением Решение. Зададим первый член последовательности: пусть 4. Доказать, что последовательность с общим членом Решение. Для убывающей последовательности выполняется неравенство
Тогда 5. Доказать, что последовательность Решение. Очевидно,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 изображаются одной и той же кривой. Если же в обратной функции
изображаются одной и той же кривой. Если же в обратной функции  симметричны относительно биссектрисы 1-3 координатных углов.
симметричны относительно биссектрисы 1-3 координатных углов. -синий и
-синий и 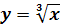 - зеленый.
- зеленый.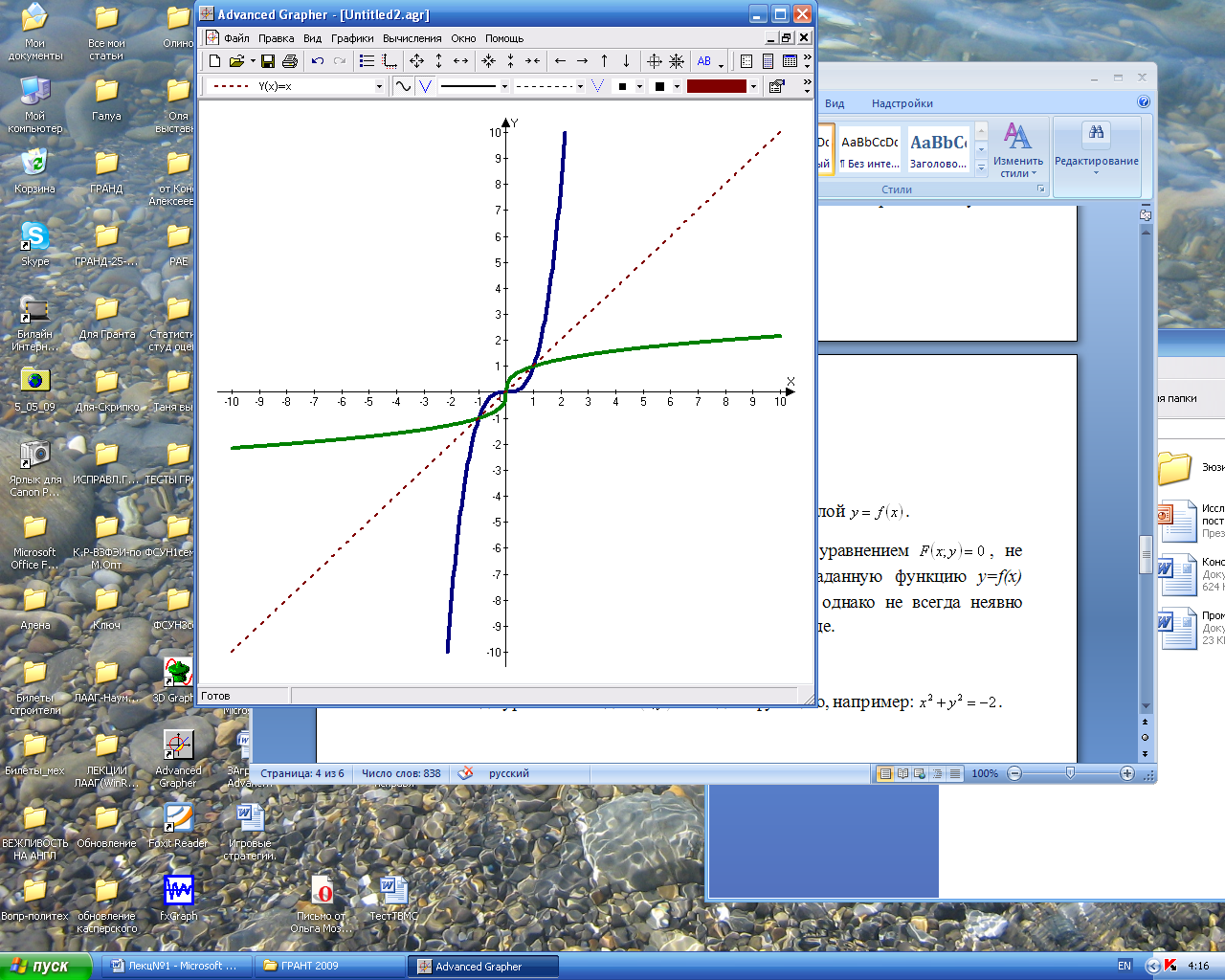
 .
. , не разрешенным относительно
, не разрешенным относительно  . Любую явно заданную функцию y=f(x) можно представить в неявном виде: y-f(x)=0 , однако не всегда неявно заданную функцию можно представить в явном виде.
. Любую явно заданную функцию y=f(x) можно представить в неявном виде: y-f(x)=0 , однако не всегда неявно заданную функцию можно представить в явном виде. .
. 


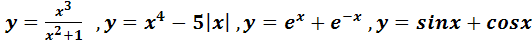

 составить сложные функции:f(g(x)) и g(f(x)).
составить сложные функции:f(g(x)) и g(f(x)).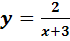

 )
)

 и g(f(x))=
и g(f(x))= 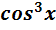 .)
.)
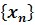 называется возрастающей (убывающей), если каждый ее член, начиная со второго, больше (меньше) предыдущего, т. е. если для любого n выполняется неравенство
называется возрастающей (убывающей), если каждый ее член, начиная со второго, больше (меньше) предыдущего, т. е. если для любого n выполняется неравенство  >
>  (
(  <
<  ).
). .
. М (
М ( 
 т). Числа М и т называются соответственно верхней и нижней границами последовательности
т). Числа М и т называются соответственно верхней и нижней границами последовательности 

 .
. . Найти первые члены последовательности.
. Найти первые члены последовательности. . Полагая в рекуррентном соотношении n=2, получим
. Полагая в рекуррентном соотношении n=2, получим  При n =3, 4, 5 соответственно находим
При n =3, 4, 5 соответственно находим  . В результате получаем последовательность 2, 7, 22, 67, 202, ... .
. В результате получаем последовательность 2, 7, 22, 67, 202, ... . монотонно убывает.
монотонно убывает. , или
, или  .Запишем (
.Запишем (  )-й член последовательности:
)-й член последовательности:
 , так как
, так как  <
<  при любом натуральном п. Следовательно, данная последовательность является убывающей.
при любом натуральном п. Следовательно, данная последовательность является убывающей. ограничена снизу и сверху.
ограничена снизу и сверху. > 1, т. е. последовательность ограничена снизу. С другой стороны имеем
> 1, т. е. последовательность ограничена снизу. С другой стороны имеем  , где
, где  – правильная дробь, и, следовательно, 1+
– правильная дробь, и, следовательно, 1+