
|
|
Методические указания к задаче 35 - 37В задаче 37 определим потери напора на участке А-В до подключения к нему лупинга. Найдем соотношение между Q1 и Q2 после подключения лупинга и определим их величины. Определим потери напора во всем разветвлении через потери напора в лупинге и вычислим относительное изменение потерь напора. Задачу 35 решают графоаналитическим способом. Сначала задают несколько произвольных диаметров, после по известному расходу определяют скорость потока. Затем определяют режим движения и в зависимости от него – коэффициент гидравлического сопротивления по одной из формул. После этого, подставляя все известные величины в формулу Дарси – Вейсбаха, находят для каждого из принятых диаметров потери давления Рi. В задаче 36 в начале определяют скорость нефти до первой перекачки, потом режим движения, потери давления, и т.д. на втором, третьем, четвертом участках. Общий перепад давлений получают при сложении перепадов на отдельных участках. Методические указания к задачам №39, 40 В начале определить скорость движения бензина с использованием уравнения неразрывности потока
где Q – расход бензина, м3/с v – скорость движения, м/с S – площадь живого сечения, м2. Затем необходимо определить скорость распространения волны гидравлического удара и повышение давления при прямом гидравлическом ударе. Также нужно определить скорость течения воды в трубе до закрытия задвижки, исходя из уравнения Бернулли:
где Н – напор воды в баке, м
g – ускорение свободного падения, м/с2. Затем определяются скорости распространения волны гидравлического удара С, м/с и повышение давления ∆Р, Па в стальной трубе и в чугунной трубе – С1, м/с и ∆Р1, Па и сравниваются ∆Р и ∆Р1. Методические указания к задачам №44, 49 При решении задачи определяем начальный и конечный напоры, число Рейнольдса, коэффициент расхода, время истечения. Методические указания к задачам № 50, 46 Необходимо воспользоваться формулами для определения движения вязко-пластичной жидкости, разности давлений КОНТРОЛЬНАЯ РАБОТА По дисциплине гидравлика предусмотрено выполнение 7 задач в соответствии со своим вариантом. В задачах в исходных данных: i – соответствует последней цифре шифра k – соответствует номеру шифра Например: ваш шифр 30, тогда i – 0, k – 3; или шифр 5, тогда i – 5, k – 0. Задача 1. Определить плотности воды и нефти при 4 ºС, если известно, что (10 + k) л воды при 4 ºС имеют массу (10 + k) кг, а масса того же объема нефти равна (8,2 + i) кг. Сравнить плотность нефти с плотностью воды. Задача 2. Цистерна заполнена нефтью плотностью ρсм = 850 кг/м3. Диаметр цистерны d = (3 +0,1 i) м, длина l = 6 м. Определить массу жидкости в цистерне. Задача 3. Плотность нефти при температуре (15 0 C равна 828 кг/м3. Условная вязкость ее при температуре (22+ k)0 C равна 6,40Е, коэффициент температурного расширения 0,00072 К-1. Определить абсолютную вязкость нефти при температуре (22+ k)0 C. Задача 4.При испытании прочности баллона он был заполнен водой при давлении (60 + k) кгс/см2. Через некоторое время в результате утечки части воды через неплотности давление в баллоне снизилось вдвое. Диаметр баллона (350 мм, высота (1200 + 8k) мм. Определить объем воды, вытекшей при испытании. Задача 5.Условная вязкость битумной эмульсии при температуре (20 + 0,2 i) 0С равна (14+ 0,5 i) 0Е , плотность равна 1230 кг/м3. Определить динамическую вязкость битумной эмульсии при той же температуре. Задача 6. Баллон, вместимость которого равна (36 + 2k) дм3, заполнен нефтью и плотно закрыт при давлении (1 ат. Какое количество нефти необходимо закачать в баллон дополнительно, чтобы давление в нем повысилось в 25 раз? Задача 7. (23,5 тонн при температуре 30 С занимают объем (33,25+ 0,1k) м3. Какой объем будет занимать это же количество бензина при температуре 170 С, если давление не изменится? Коэффициент температурного расширения бензина 0,00065 К-1. Задача 8. При испытании прочности резервуара он был заполнен водой при давлении (50 – 0,2i) ат. Через некоторое время в результате утечки части воды через неплотности давление понизилось до (11,5 + 0,2i) ат. Определить объем воды, вытекшей за время испытания. Вместимость резервуара равна (20 м3. Задача 9. Бензин весом (43,5 – 0,2i) тонны при температуре 15 С занимает объем 33,5 м3. Какой объем будет занимать это же количество бензина при температуре (6 С? Коэффициент температурного расширения бензина 0,00065 град-1. Задача 10. В резервуар закачено (15 – 0,2i) м3 нефти удельного веса 800 кгс/м3 и (16 – 0,2i) м3 нефти неизвестного удельного веса. Удельный вес смеси стал равным 824 кгс/м3. Определить удельный вес долитой нефти. Задача 11. Для испытания резервуара на прочность он заполнен водой под давлением (50 ат. Вследствие утечки воды давление в резервуаре понизилось до (42 - 0,1k) ат. Сколько воды вытекло из резервуара, если он имеет форму цилиндра с диаметром 500 см и высотой 800 см? Задача 12. Определить, насколько поднимется уровень нефти в цилиндрическом резервуаре при увеличении температуры от 15 до 40 ºС. Плотность нефти при 15 ºС ρ15 = 900 кг/м3. Диаметр резервуара d = (10 м; нефть заполняет резервуар при 15 ºС до высоты H = (12 - 0,1k) м. Коэффициент теплового объемного расширения нефти βТ = 6,4∙10-4 1/градус. Расширение резервуара не учитывается. Задача 13. Вода поступает в насос по всасывающей трубе, работающей под вакуумом. Минимальное абсолютное давление перед входом в насос p = (4 кПа. Температура перекачиваемой воды поднялась до 30 ºС. Будет ли наблюдаться в этом случае явление кипения? Задача 14.В закрытом резервуаре (рис.23) с нефтью плотностью ρ = 880 кг/м3 вакуумметр, установленный на его крышке, показывает pв = (1,18 + 0,2k)∙104 Па. Определить показание манометра pм, присоединенного к резервуару на глубине H = 6 м от поверхности жидкости, и положение пьезометрической плоскости.
Задача 16. Найти силу давления воды на дно сосуда диаметром D = (1 + 0,2k) м (рис. 22), если глубина H = (0,7 + 0,2k) м, вес поршня G = 300 H, d = 0,5 м.
рис. 24 рис. 25 Задача 18. Наклонный прямоугольный щит плотины шарнирно закреплен на оси О (рис. 26). При каком уровне воды H щит опрокинется, если угол наклона щита α = (60 + 0,9i)º, а расстояние от его нижней кромки до оси шарнира а = (1,3 + 0,2i) м. Вес щита не учитывать. Задача 19. Определить силу давления жидкости на торцевую плоскую стенку горизонтальной цилиндрической цистерны (рис. 27) диаметром d = (2,4 + 0,2k) м, заполненной бензином плотностью ρ = 760 кг/м3, если уровень бензина в горловине находится на расстоянии H = (2,7+ 0,2k) м от дна. Цистерна герметично закрыта и избыточное давление на поверхности жидкости составляет (40 + 0,2i) кПа. Найти также положение центра давления относительно центра тяжести стенки. Задача 20. Закрытый резервуар высотой Н = (10 - 0,1i) м (рис. 25) разделен на два отсека вертикальной прямоугольной перегородкой шириной b = 4 м. В левом отсеке уровень нефти Н1 = (8 - 0,1k) м (ρн = 850 кг/м3), в правом уровень воды Н1 = (5 - 0,1k) м (ρв = 1000 кг/м3). Избыточное давление паров над нефтью pи 1 = 19,6 кПа. Определить равнодействующую сил давления на перегородку и точку ее приложения. Указание. В левом отсеке, кроме силы давления нефти и паров, на смочен
рис. 26 рис. 27 Задача 21. Шаровой резервуар диаметром d = (1 + 0,2k) м целиком заполнен жидкостью плотностью ρ = 103 кг/м3. В верхней точке жидкости в резервуаре давление атмосферное. Определить величины и направления сил, действующих на верхнюю и боковую полусферы.
Задача 23. Из напорного бака вода течет по трубе диаметром d1 = (20 + 0,2k) мм и затем вытекает в атмосферу через насадок (брандспойт) с диаметром выходного отверстия d2 = 10 мм. Избыточное давление в баке Ро= (0,18+ 0,1k)МПа. Пренебрегая потерями, определить скорость течения воды в трубе ϑ1 и на выходе из насадка ϑ2. Высота жидкости над осью трубы Н = 1,6 м (рис. 29). Задача 24. Определить силу, действующую на деревянный брус длиной L = (0,5 + 0,3k) м и площадью поперечного сечения F= (0,02 + 0,2k) м2, полностью погруженный в воду. Плотность бруса принять ρб = 600 кг/м3. Задача 25. Построить эпюру гидростатического давления для плоской стенки, графически определить силу давления жидкости на стенку и место ее приложения, если высота смоченной поверхности А, давление на свободную поверхность жидкости Ро, ширина стенки в, плотность жидкости ρж.
Задача 26. Открытая емкость в виде усеченного конуса стоит на меньшем основании и полностью заполнена жидкостью с плотностью ρ = 1100 кг/м3. Определить результирующую силу давления жидкости на дно емкости и силу давления емкости на горизонтальную опору. Высота емкости h = (2 + 0,2k)м, диаметр нижнего сечения d1 = (2 + 0,2k)м, диаметр верхнего сечения d2 = 3 м. Задача 27. Вертикальный цилиндрический резервуар емкостью F = (1000+ 20k) m3, высотой Н = 13м заполнен нефтью с плотностью ρн = 880 кг/м3. Определить силы давления нефти на боковую стенку и дно резервуара. Задача 28. Какой объем бензина (ρ = 740 кг/м3) можно залить в железнодорожную цистерну внутренним объемом (50 + 0,2k)м3 и массой (23 + 0,2i) т, чтобы она еще сохраняла плавучесть в пресной воде? Задача 26. По трубопроводу диаметром d = (0,15 + 0,25k) м перекачивается нефть плотностью ρ = 950 кг/м3 в количестве (1500 + 28k)т/сут. Определить объемный расход Q и среднюю скорость течения υ. Задача 29. Из открытого резервуара с постоянным уровнем (рис. 30) идеальная жидкость по горизонтальной трубе вытекает в атмосферу, Н = (1,6 + 0,1k) м; d1 = 0,15 м; d2 = 0,075 м. Определить уровень жидкости в пьезометре h.
рис. 30 рис. 31 Задача 30. Поток воды у входа в турбину (рис. 31) в сечении 1 -1 имеет скорость υ1 = (3 + 0,2i) м/с и давление p1 = 2 МПа. На выходе из турбины сечение 2 – 2 υ2 = (1,2 + 0,1k) м/с, p2 = 0,05 МПа. Расход воды через турбину Q = (9 + 0,2k)·103 м3/ч. Расстояние между сечениями h = 0,5 м. Определить мощность N на валу турбины, если к.п.д. турбины η = 0,85. Задача 31. По трубопроводу перекачивается нефть плотностью ρ = 910 кг/м3 в количестве Q = (0,04 + 0,1k) м3/с. Сечение 2 – 2 расположено выше сечения 1 -1 на 10 м. Диаметры трубы d1 = (0,3 + 0,1k) м; d2 = 0,2 м; давления p1 = 1,5 МПа, p2 = 1 МПа. Определить потерю напора h1-2. Задача 32. По горизонтальной трубе течет жидкость плотностью ρ = 103 кг/м3, расход Q = 2,5·10-3 м3/с, диаметр D=0,05 м. Определить, пренебрегая потерями напора, диаметр d, если разность давлений р1 – р2 =15 кПа. Задача 33. По трубе d = (0,1 + 0,1k)м течет вода. Определить максимальные скорость течения υ и расход Q, при которых режим течения будет оставаться ламинарным. Вязкость воды η = 10-3 кг/м·с. Задача 34. При течении нефти в трубопроводе диаметром d = (0,2 + 0,1k) м массовый расход QМ = (35 + 11k) т/ч. Нефть заполняет сечение трубопровода до высоты h = d/2. Вязкость нефти η = 0,12 кг/(м · с). Определить режим течения. Задача 35. Известен перепад давления на сборном коллекторе ∆Р=3 МПа, расход нефти Q = (400 + 5k) т/сут, разность высот отметок конца и начала коллектора ∆z = 20 м, длина его (4 + 0,1k) км, плотность нефти ρ = 0,8 т/м3, вязкость ν = 20 мм2/с. Необходимо определить диаметр коллектора. Задача 36. В начало сборного коллектора длиной L = 10 км, диаметром (0,2 + 0,1k) м подают товарную нефть в количестве Q = Qт + Qп = 180 т/ч, вязкостью μ = 20 мПа·с и ρ = 800 кг/м3. из сбороного коллектора нефть отбирают в трех точках соответственно с q1 = 20 т/ч, q2 = 50 т/ч, q3 = 100 т/ч. Расстояние от начала коллектора и до точек отбора нефти следующие: L1 = 4 км, L2 = 200 м, L3 = 3 км. Определить общий перепад давления, если начальное давление равно (1,6 + 0,15k) МПа. Сборный коллектор проложен горизонтально и местных сопротивлений не имеет. Задача 37. Определить относительное изменение потерь напора на участке А-В = (5 + 0,1k) км (d1 = 200 мм), если к нему подключить лупинг той же длины (d2 = 260 мм). Трубы сварные новые, местными сопротивлениями пренебречь.
Задача 38. После очистки всасывающей линии (l = 10 м, d = 200 мм) насосной установки (к.п.д. ηнас = (0,65 + 0,01k)) коэффициент местного сопротивления фильтра ζф уменьшился с 40 до 10, а эквивалентная шероховатость труб с 1 до 0,1 мм. Подача насоса Q = (0,07 + 0,1k) м3/с. Определить годовую экономию электроэнергии от этой операции. Температура воды 20°С. Задача 39. Насос, оборудованный воздушным колпаком, перекачивает бензин по трубопроводу длиной l = (5 + 0,1k) км, диаметром d = (75 + 0,1i) мм, δ = 5 мм в количестве Q = 9·10-3 м3/с. Плотность бензина ρ = 740 кг/м3, модуль упругости бензина К = 1,1·109 Па, Е = 2·1011 Па. Определить, за какое время необходимо перекрыть задвижку, чтобы ударное повышение давления не превосходило 1 МПа. Задача 40. По трубопроводу длиной lпр = (20 + 0,1i) м, диаметром d = (0,5 + 0,1k) м, δ = 3,5 мм, соединенному с баком, под напором Н = 2,5 м течет вода (К = 2·109 Па). В некоторый момент времени происходит мгновенное перекрытие потока в конце трубопровода. Найти скорость распространения волны гидравлического удара и величину ударного повышения давления, если труба стальная (Е = 2·1011 Па). Коэффициент гидравлического сопротивления принять равным 0,03. Как изменится ударное повышение давления, если стальную трубу заменить чугунной тех же размеров (Е = 0,98·1011Па)?
Задача 42. По приведенному на рис. 34 сифонному сливу (l = 50 м, d = (100 + 10k) мм, ∆ = 0,06 мм) подается топливо (ρ = 840 кг/м3, v = 5,5·10-6 м2/с) при разности отметок уровней в резервуарах Н1 = 1,38 м. На сливе имеются фильтр для светлых нефтепродуктов, два колена и вентиль; Н2 = (3 + 0,1k) м, Н3 = 2 м, давление насыщенных паров при температуре перекачки рп = 2 кПа, ра = 105 Па. Определить расход жидкости и проверить условие нормальной работы сифона.
Задача 43. Минеральное масло (ρ = 840 кг/м3, v = 10-4 м2/с) по горизонтальному трубопроводу (см. рис. 35) подается к раздаточным пунктам С, Е и F. Расходы масла в этих пунктах: QС = (10,6 + 0,1k) дм3/с; QЕ = (6,8 + 0,1i) дм3/с; QF = 14 дм3/с; концевые свободные напоры: НС = 67 м, НЕ = 0, НF = 7 м; длины участков трубопровода lАВ = 3 м, lВС = (1 + k) км, lBD = 2 км; lDE = (1,5 + i) км, lDF = 1,5 км. Насос при заданных расходам в пунктах раздачи может создать напор НА = 100 м, в наличии имеются новые сварные трубы диаметрами 80, 100, 125, 200, 250 мм. Подобрать диаметры всех участков трубопровода, считая потери напора в местных сопротивлениях пренебрежимо малыми. Допустимое расхождение между реальными напорами НА и расчетным – не более 5%.
Задача 44. Определить время опорожнения вертикального цилиндрического резервуара D = (8 + 0,5k)м, заполненного нефтью до уровня Н= (10 + k) м. Истечение осуществляется через цилиндрический внешний насадок (do = 5 см и длина / = 20 см). Кинематическая вязкость нефти v = 120 мм2/с, плотность ρ = 880 кг/м3. Задача 45. В горизонтальном трубопроводе (l =(10 + i)км, d = (250 мм) находится нефть, которая имеет свойства вязко-пластичной жидкости с начальным напряжением сдвига τо = (8 + 0,1k) Па. Определить разность давлений на концах трубопровода ∆РО, при которой начнется движение нефти. Задача 46. Определить дебит нефтяной скважины (rс = 0,1 м), расположенной в центре пласта (RK = 500 м, h = 15 м), если пластовое давление Рк =(17 + k) МПа; давление в скважине Рс = (14 + i) МПа; динамическая вязкость μ =0,1 Па·с; плотность нефти ρ = 850 кг/м3; коэффициент проницаемости K = 1,0 мкм2; коэффициент пористости m = 0,2. Нефть считать ньютоновской жидкостью. Задача 47. По трубопроводу диаметром
рис. 36
Задача 48. Цилиндрический сосуд, заполненный жидкостью, плотность которой ρ = 900 кг/м3, движется с ускорением а = 4g. Определить силы, действующие на крышки А и Б, если l = 1 м и d = (0,5 + 0,1k) м. Давление в точке 1 равно атмосферному (рис. 37). рис. 37 Задача 49. Из цилиндрического вертикального резервуара - отстойника (D = (3,5 + 0,1k) м), предназначенного для разделения нефти и пластовой воды, через донную вертикальную трубу (L = (0,5 + 0,1i) м, d = 0,125 м) сливается вода (рв = 1100 кг/м3, v = 1 мм2/с). Начальный уровень воды в резервуаре he = 4 м, нефти) hн = 1 м. Необходимо определить время слива воды, считая, что имеется четкая граница раздела воды и нефти (р = 880 кг/м3). Задача 50. Решить задачу 46 при условии, что нефть является вязко-пластичной жидкостью с начальным напряжением сдвига τо = 5 Па.
Плотности некоторых жидкостей

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,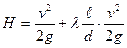
 , d – размеры трубопровода, м
, d – размеры трубопровода, м - коэффициент гидравлического сопротивления
- коэффициент гидравлического сопротивления и расхода нефти, потом проверить режим течения по обобщенной формуле.
и расхода нефти, потом проверить режим течения по обобщенной формуле. Задача 15. Найти избыточное давление в сосуде А с водой по показаниям многоступенчатого двухжидкостного ртутного манометра (рис. 21): h1 = (82 - 0,1k) см; h2 = (39– 0,2i) см; h3 = 54 см; h4 = (41 + 0,2k) см; h5 = 100 см; ρ = 103 кг/м3; ρр = 1,36∙104 кг/м3.
Задача 15. Найти избыточное давление в сосуде А с водой по показаниям многоступенчатого двухжидкостного ртутного манометра (рис. 21): h1 = (82 - 0,1k) см; h2 = (39– 0,2i) см; h3 = 54 см; h4 = (41 + 0,2k) см; h5 = 100 см; ρ = 103 кг/м3; ρр = 1,36∙104 кг/м3. рис. 22 рис. 23
рис. 22 рис. 23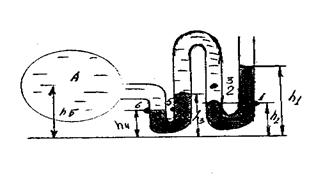

 Задача 17. Вертикальный щит А (рис. 24), перекрывающий водослив плотины, может перемещаться в пазах B вверх и вниз. Глубина жидкости H = (1,4 + 0,2i) м, ширина щита b = (2,6 + 0,2k) м. Какую силу нужно приложить, чтобы поднять щит, если вес его G = (32 + 0,1i) кН, а коэффициент трения между щитом и поверхностью пазов f = 0,3.
Задача 17. Вертикальный щит А (рис. 24), перекрывающий водослив плотины, может перемещаться в пазах B вверх и вниз. Глубина жидкости H = (1,4 + 0,2i) м, ширина щита b = (2,6 + 0,2k) м. Какую силу нужно приложить, чтобы поднять щит, если вес его G = (32 + 0,1i) кН, а коэффициент трения между щитом и поверхностью пазов f = 0,3. ную часть перегородки, нужно учесть силу давления паров на не смоченную часть стенки.
ную часть перегородки, нужно учесть силу давления паров на не смоченную часть стенки.

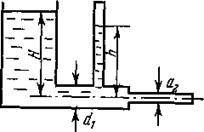
 Задача 22. Горизонтальная цилиндрическая цистерна с полусферическими днищами целиком заполнена топливом (ρ = 800 кг/м3). Давление в верхней части цистерны, измеряемое манометром, pм = (14,7 + 0,2k) кПа, длина цистерны l = 5 м, ее диаметр d = 3 м (рис. 1.31). Определить величины сил давления, растягивающих цистерну в сечениях А – А и В – В, и положение линий их действия.
Задача 22. Горизонтальная цилиндрическая цистерна с полусферическими днищами целиком заполнена топливом (ρ = 800 кг/м3). Давление в верхней части цистерны, измеряемое манометром, pм = (14,7 + 0,2k) кПа, длина цистерны l = 5 м, ее диаметр d = 3 м (рис. 1.31). Определить величины сил давления, растягивающих цистерну в сечениях А – А и В – В, и положение линий их действия. рис. 28 рис. 29
рис. 28 рис. 29

 Задача 41.Вода (t = 20°С) перетекает из резервуара А в резервуар В, давления на поверхности жидкости в которых одинаковы (рис. 33). Соединительный трубопровод состоит из двух последовательно соединенных участков новых бесшовных труб (l1 = (200 + 5k) м, d1 = 100 мм и l2 = (150 + 3k)м, d2 = 80 мм), для обеих труб lэкв = 0,05l, h = 3 м. Определить расход воды.
Задача 41.Вода (t = 20°С) перетекает из резервуара А в резервуар В, давления на поверхности жидкости в которых одинаковы (рис. 33). Соединительный трубопровод состоит из двух последовательно соединенных участков новых бесшовных труб (l1 = (200 + 5k) м, d1 = 100 мм и l2 = (150 + 3k)м, d2 = 80 мм), для обеих труб lэкв = 0,05l, h = 3 м. Определить расход воды. рис. 34
рис. 34 рис. 35
рис. 35 = (30 + k) мм и длиной
= (30 + k) мм и длиной  = (5 + 0,1k) м движется вода. Чему равен напор
= (5 + 0,1k) м движется вода. Чему равен напор  = (3 + 0,2k) м, при котором происходит смена ламинарного режима турбулентным? Местные потери напора не учитывать. Температура жидкости
= (3 + 0,2k) м, при котором происходит смена ламинарного режима турбулентным? Местные потери напора не учитывать. Температура жидкости  .
.
