
|
|
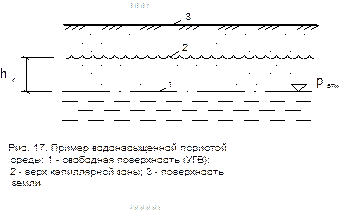
Определения, термины и закономерностиФильтрацией называется движение жидкости или газа в пористой среде. Под средой подразумевается твёрдая фаза. Большинство сред являются пуристыми: грунты, бетон, кирпич и т.д. Но не в каждой пористой среде происходит фильтрация. Движение жидкости или газа происходит только по сообщающимся между собой порам (не замкнутым). Кроме того, размер пор должен быть достаточным для пропуска жидкости или газа. Среды с такими порами называются фильтрующими или проницаемыми. Примерами фильтрующих сред могут служить некоторые грунты (пески, сэпеси, суглънки), строительные материалы (щебень, пористый бетон, кирпичная кладка). Проницаемость пористой среды определяется опытным путём. Водоупором называют грунт, практически не пропускающий воду. Глины часто являются водоупорными, так как поры в них замкнутые и малого размера. Непроницаемый же строительный материал принято именовать гидроизоляционным (а не водоупорным). Так, в качестве гидроизоляции используют цементный раствор, различные битумные мастики, толь, рубероид. Теория фильтрации применительно к водоснабжению и строительству рассматривает закономерности фильтрации воды с целью проведения количественных расчётов: — притока подземных вод к водозаборным сооружениям (скважинам, колодцам и т.д.); — работы фильтров на станции водоподготовки при приготовлении питьевой воды; — при прогнозах подтопления подземными водами территорий застройки; — при выборе систем строительного водопонижения для котлованов, траншей или подземных проходок в водонасыщенных грунтах; — при проектировании дренажных систем (дренажйй), понижающих уровень грунтовых вод (УГВ) для защиты подземных сооружений и помещений зданий от подтопления. Термины теории фильтрации во многом совпадают с гидравлическими. Движение жидкости при фильтрации принято рассматривать каксплошной поток, будто бы твёрдых частиц пористой среды нет. Поэтому фильтрационные потоки формально имеют сходство с потоками в трубах и каналах. Перечислим элементы фильтрационных потоков (термины). Свободная поверхность — это граница раздела между полностью водонасыщенной пористой средой и осушенной её частью (рис. 17). На этой границе давление равно атмосферному pатм . Особенностью является то, что над свободной поверхностью в пористой среде имеется капиллярная зона высотой hк , которая не полностью водонасыщена, но где часть влаги удерживается капиллярными силами пор.
Все фильтрационные потоки делятся на: — напорные (без свободной поверхности); — безнапорные(со свободной поверхостью). Примерами напорных фильтрационных потоков могут служить артезианские подземные воды, которые при бурении скважин дают фонтан. Примером безнапорных потоков является грунтовые воды, просачивающиеся в котлованы и траншеи, что рассмотрено ниже. Определения линии тока, площади живого сечения потока S (м2) и фильтрационного расхода Q (м3/сут) можно использовать гидравлические. Но в отношении S нужно учитывать, что это площадь вся — и пор, и твёрдой фазы, так как в теории фильтрации принято считать поток сплошным (условие сплошности). Движение потока при фильтрации всегда происходит под влиянием разности напоров ∆H (м), от большего напора к меньшему. Фильтрационный напор H (м) находится формально как гидростатический:
так как в нём обычно не учитывается скоростная составляющая напора hv (см. гидродинамический напор) из-за малых скоростей движения жидкости по порам. В грунтовых водах напор в метрах по высоте может отсчитываться от водоупора, если поверхность последнего можно принять за горизонтальную плоскость (рис. 18), но может также приниматься как абсолютная геодезическая отметка свободной поверхности потока.
I = DH / l .
Скоростью фильтрацииvф (м/сут) называется отношение фильтрационного расхода Q (м3/сут) к площади живого сечения потока S (м2): vф = Q/S . Теперь, имея вышеперечисленные термины теории фильтрации, приведём её основной закон. Закон Дарсъ (основной закон фильтрации) связывает скорость фильтрации vф (м/сут) с коэффициентом фильтрации пористой среды kф (м/сут), разностью напоров (потерями напора) ∆H (м) и длиной пути фильтрации l так:
Фильтрационные характеристики пористых сред определяются опытным путём. Некоторые из них приведены в таблице. Коэффициент фильтрации kф характеризует проницаемость пористой среды. Коэффициент водоотдачи в (величина безразмерная) показывает, сколько воды может отдать при осушении грунт в долях единицы его объёма.
Фильтрационные расчёты В строительной практике большинство фильтрационных расчётов связано с определением водопритока грунтовых вод Q (м3/сут) в траншеи и котлованы, с целью заблаговременного подбора насосов для водоотлива так, чтобы их производительность была не менее величины Q. Грунтовые воды (см. рис. 18) — это подземный водоносный горизонт, имеющий свободную поверхность (т.е. уровень грунтовых вод — УГВ) и залегающий на первом от поверхности земли водоупоре. Таким образом, грунтовые воды являются безнапорными. Они залегают в проницаемых грунтах (песках, сэпесях, суглинках), имеющих некоторый коэффициент фильтрации kф. Они имеют некоторую естественную мощность He , в пределах которой грунт полностью водонасыщен. УГВ регистрируется скважинами, открытыми в атмосферу (скважинами-пьезометрами). Закон Дарси служит основой для получения расчётных формул при различных случаях фильтрации, которые могут наблюдаться на практике. В качестве примера покажем, как можно вывести формулу для определения притока грунтовых вод в траншею при использовании закона Дарси и гидравлических принципов. На рис. 19 изображена траншея длиной В. В нашем примере своим дном она доходит до водоупора. Прибывающая в траншею грунтовая вода постоянно откачивается насосом с расходом Q. Этот расход складывается из правого Qп и левого Qл водопритоков грунтовых вод. Движение грунтовых вод к траншее происходит из-за разности напоров в водоносном пласте и траншее ∆H=He–Hт. Напоры отсчитываем от поверхности водоупора. Длина пути фильтрации Lt(см. рис. 19,б) называется зоной влияния откачки. В пределах этой зоны естественный УГВ постепенно понижается в сторону траншеи и носит название кривой депрессии. Зонавлиянияоткачки Lt с течением времени увеличивается. Это происходит из-за осушения грунта вблизи траншеи, кривая депрессии становится более пологой и длинной . Величину Lt (м) можно определить так:
где t — время от начала откачки, сут. Распишем водоприток грунтовых вод в траншею: Q = Qп+ Qл = vфS + vфS.
Скорость фильтрации по закону Дарсъ выражается так:
Среднюю величину площади живого сечения фильтрационного потока переменной высоты в пределах кривой депрессии (см. рис. 19,б) можно записать так:
Подставляя vф и S в выражение для Q , после элементарных выкладок получим формулу для определения притока грунтовых вод в траншею:
Приток грунтовых вод, фильтрующихся в котлован (рис. 20), колодец или скважину, можно определить по формуле (приводится без вывода)
где Hе —естественный напор в грунтовых водах (их мощность); Hк — напор в котловане (слой воды в котловане); Rt — радиус влияния откачки; rк — радиус котлована; = 3,14 ; ln — натуральный логарифм. Величину Rt можно найти так:
где t — время от начала откачки, сут. Котлован с реальной плановой конфигурацией площадью F приводится к равновеликому условно круглому котловану радиусом
Водоприток Q в траншеи и котлованы максимален в начале откачки и уменьшается с течением времени одновременно с увеличением Ltили Rt. Это объяснимо постепенной сработкой водоносного горизонта (осушением грунта) вблизи строительной выемки. Вопросы для самоконтроля 1. Перечислить простейшие случаи фильтрации несжимаемой жидкости и газа. 2. Дать определение коэффициента фильтрации. 3. Сформулировать основные законы фильтрации. 4. Безнапорное и напорное движение жидкости в пористой среде.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, Фильтрационный поток по ходу движения всегда теряет напор из-за внутреннего трения жидкости. Отношение потерь напора ∆H (м) к длине пути фильтрации l (м) называется пьезометрическим уклоном или градиентом напора (величина безразмерная).
Фильтрационный поток по ходу движения всегда теряет напор из-за внутреннего трения жидкости. Отношение потерь напора ∆H (м) к длине пути фильтрации l (м) называется пьезометрическим уклоном или градиентом напора (величина безразмерная).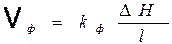 .
. ,
, .
. .
.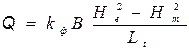 .
.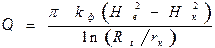
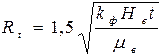 ,
,
 .
.