
|
|
Расчёт безнапорных потоковРасчёт безнапорных потоков состоит в решении совместной задачи о пропуске расхода q при допустимых скоростях потока v и геометрических уклонах iгеом днища труб, каналов и т.д. Безнапорные (со свободной поверхностью) потоки наблюдаются в канализационных трубах, дорожных лотках, каналах; в природе — в реках, ручьях. При расчёте безнапорных потоков вводится допущение о равномерном движении потока: геометрический уклон дна iгеом считается равным уклону свободной поверхности (пьезометрическому уклону) и гидравлическому уклону i . Другими словами, поверхность дна 1, свободная поверхность потока 2 и напорная линия 3 параллельны друг другу (рис. 16). Это упрощает расчёт, так как определяя гидравлический i, автоматически находят уклон дна iгеом. Подчеркнём, что безнапорный поток имеет напоры! Дело в том, что термин «безнапорный» является традиционным, правильнее же его называть «поток со свободной поверхностью». Например, на рис. 16 в точках потока А и В напоры существуют, и их отметки могут быть зарегистрированы трубками Питу соответственно НАи НВ. Разность напоров НА – НВравна линейной потере напора hl на участке потока длиной l. Величина hl по принятому допущению равна ∆z — разности высотных отметок дна в начале и конце участка, так как i = hl /l , iгеом = ∆z/l, а i = iгеом.
Местные потери напора hм возникают в безнапорных потоках так же, как и в напорных, в местах резкой деформации потока: на поворотах, в тройниках, крестовинах, местных сужениях и т.д. Однако в расчётах безнапорных потоков величины hм обычно не учитывают. При проведении гидравлического расчёта безнапорных потоков вводятся ограничения по скорости v (м/с), наполнению h/d (см. рис. 7,в) и уклону iгеом. Например, при расчёте канализационных труб должны быть выполнены три таких ограничения:
где d— внутренний диаметр трубы в мм. Для расчётабезнапорныхпотоков широко применяется формула Шези:
где R — гидравлический радиус (м); С — коэффициент Шези. Коэффициент Шези можно определить по формуле Маннинга
где n — коэффициент шероховатости стенок трубы или канала; R — гидравлический радиус, подставляемый вметрах. Скорость потока связана с расходом соотношением вида v = Q/S. Таким образом, приведённые формулы позволяют осуществлять гидравлический расчёт любых безнапорных потоков. Обычно для расчётов используются вспомогательные таблицы или номограммы, составленные на основе формулы Шези. Отметим, что формула Шези справедлива для потоков с турбулентным режимом. Таких потоков на практике подавляющее большинство. Тема 3.5 Движение жидкости в пористой среде Студент должен: знать: законы фильтрации, основы расчета простейших случаев фильтрации жидкости и газа; уметь: выполнять простейшие расчеты фильтрации жидкости и гааз, применяя справочную литературу.
Основные понятия и определения. Основной закон фильтрации и границы его применения. Простейший случай установившейся напорной фильтрации несжимаемой жтдкости. Плоско-паралельная и плоско-радиальныа фильтрация газа. Литература: 1, с. 272…284
Методические указания При изучении темы обратить внимание, что движение жидкости через пористую среду называют фильтрацией. необходимо знать такие определения и величины, как коэффициент пористости – m, коэффициент просветности – n, истинная скорость движения жидкости, скорость фильтрации. Основным законом фильтрации является закон Дарси, в который входит коэффициент фильтрации kФ. он зависит от свойств породы и жидкости и используется для расчетов фильтрации 1 – фазных жидкостей. При фильтрации многофазных жидкостей используют коэффициент проницаемости k. Необходимо знать взаимосвязь этих коэффициентов и единицы их измерения. При рассмотрении простейших случаев фильтрации необходимо иметь понятие параллельно-прямолинейной фильтрации и плоско-радиальной фильтрации жидкости и газа, знать формулы для определения дебита, скорости фильтрации, законы распределения давления по пласту, что такое депрессия, знать формулу Дарси. Теория фильтрации 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


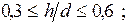
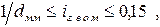
 ,
, ,
,