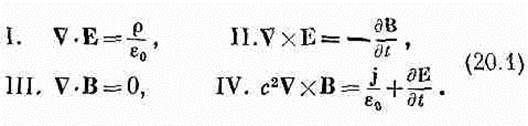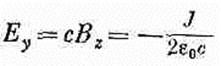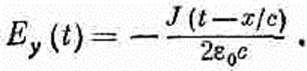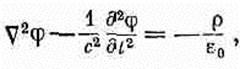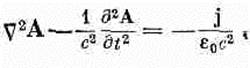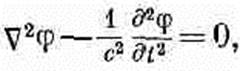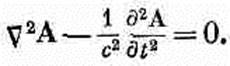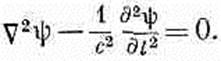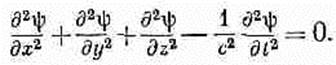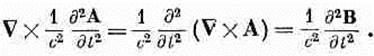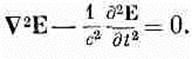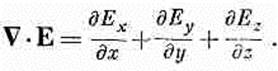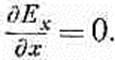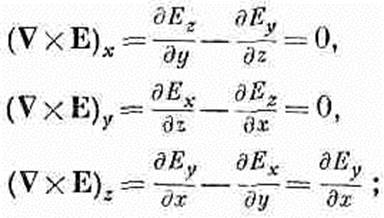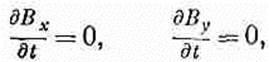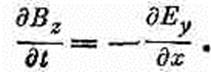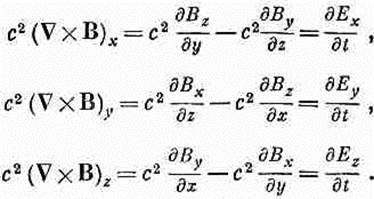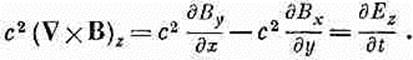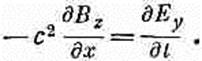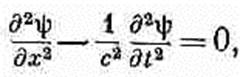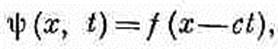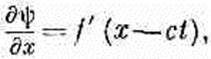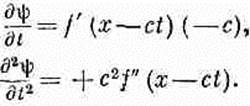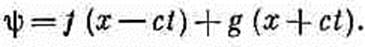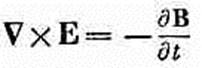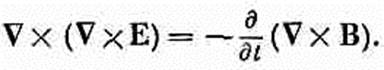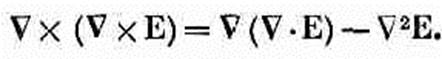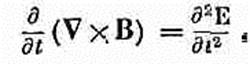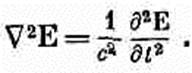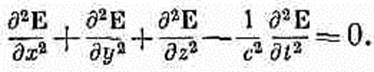|
|
Волны в пустом пространстве; плоские волны
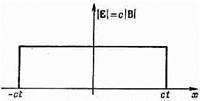
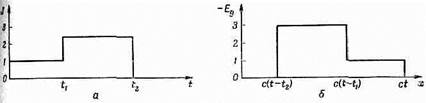
(20.2) для положительных x, меньших ct. Для больших x поля равны нулю. Равные по величине поля простираются на то же расстояние от плоскости в направлении отрицательных y. На фиг. 20.1 показан график зависимости величины полей от x в момент t. С течением времени «волновой фронт» в ct распространяется вдоль х с постоянной скоростью с.
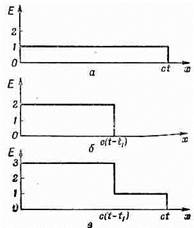
Фиг. 20.1. Зависимость электрического и магнитного полей от х через t сек после того, как была включена заряженная плоскость. Теперь представим себе такую последовательность событий. На мгновение мы включаем ток единичной силы, а затем внезапно увеличиваем его силу втрое и поддерживаем его на этом уровне. Как же будут теперь выглядеть поля? Это можно узнать таким образом. Во-первых, надо представить ток с единичной силой, включенный при t=0 и больше не менявшийся. Тогда поля при положительных х будут иметь вид, представленный на фиг. 20.2, а. Затем надо задать себе вопрос, что произойдет, если в момент t1 включить постоянный ток силой в две единицы? В этом случае поля станут вдвое больше, чем прежде, но отойдут по х только на промежуток c(t-t1) (фиг. 20.2, б). Складывая эти два решения (по принципу суперпозиции), мы получаем, что сумма источников — это ток силой в одну единицу с момента нуль до момента t1 и ток в три единицы в более поздние моменты. В момент t поля меняются вдоль х так, как показано на фиг. 20.2, в. Возьмем теперь более сложную задачу. Рассмотрим ток, имевший сначала силу в одну единицу, а затем достигший силы в три единицы и выключенный. Каковы будут поля от такого тока? Решение можно получить точно так же, как и раньше,
Фиг. 20.2. Электрическое поле плоскости с током. а — одна единица тока включена в момент t=0; б—две единицы тока включены в момент t=t1; в — суперпозиция а и б.
Фиг. 20.3. Если сила источника тока меняется так, как на рисунке (а), то в момент t электрическое поле как функция от х приобретает другой вид (б). т. е. складывая решения трех разных задач. Сперва найдем поля постоянного тока единичной силы (эту задачу мы уже решали). Потом узнаем поля от тока двойной силы. И, наконец, возьмем решение для полей токов с силой в минус три единицы. Сложив все три решения, мы получим ток силой в одну единицу от t=0 до какого-то более позднего момента, скажем, до t1, затем ток силой в три единицы до момента t2, а потом ток, равный нулю, т. е. выключенный. График зависимости тока от времени показан на фиг. 20.3, а. Складывая три решения для электрического поля, мы видим, что его изменения с расстоянием х в данный момент t подобны изображенным на фиг. 20.3, б. Поле в точности отображает собой ток. Распределение поля в пространстве есть точное отражение изменений тока со временем, но только нарисованное задом наперед. По мере того как проходит время, вся картина перемещается наружу со скоростью с, так что получается ломтик полей, который движется к положительным х и хранит в себе всю историю перемен тока. Если бы мы находились где-то на расстоянии многих километров, мы могли бы лишь по изменению электрического или магнитного поля безошибочно рассказать, как менялся ток в источнике. Заметьте также, что даже после того, как вся деятельность в источнике прекратилась и все заряды исчезли, а токи сошли на нет, наш ломтик полей продолжает свое путешествие через пространство. Получается распределение электрических и магнитных полей, которое существует независимо от токов и зарядов. Это и есть тот новый эффект, который следует из полной системы уравнений Максвелла. Мы можем, если нужно, представить только что проделанный анализ в строго математической форме, написав, что электрическое поле в данном месте и в данное время пропорционально току в источнике, но не в то же время, а в более ранний период [t-(x/с)]. Можно написать
Вас удивит, если я скажу, что мы уже выводили это уравнение раньше (с другой точки зрения), когда говорили о теории показателя преломления. Тогда нам нужно было представить себе, какие поля создаст слой колеблющихся диполей в тонком плоском диэлектрике, если диполи приводятся в движение электрическим полем падающей электромагнитной волны. Задача наша состояла в расчете комбинированного поля начальной волны и волн, излучаемых колеблющимися диполями. Как же мы смогли тогда рассчитать поля, создаваемые движущимися зарядами, не зная уравнений Максвелла? Мы тогда приняли в качестве исходной (без вывода) формулу для полей излучения, создаваемых на больших расстояниях от ускоряемого точечного заряда. Если вы заглянете в гл. 31 (вып. 3), то увидите, что выражение (31.10) — это как раз наше выражение (20.3), которое мы только что написали. Хотя прежний наш вывод относился только к большим расстояниям от источника, теперь мы видим, что тот же результат верен и вблизи источника. Сейчас мы хотим взглянуть в общем виде на поведение электрических и магнитных полей в пустом пространстве вдалеке от источников, т. е. от токов и зарядов. Очень близко от них (так близко, что источники за время запаздывания передачи не успевают сильно измениться) поля очень похожи на те, которые получились у нас в электростатике или магнитостатике. Но если перейти к таким большим расстояниям, что запаздывание станет заметным, то природа полей может радикально отличаться от тех решений, которые мы нашли. Когда поля значительно удаляются ото всех источников, они начинают в некотором смысле приобретать свой собственный характер. Так что мы вправе приступить к обсуждению поведения полей в области, где нет ни токов, ни зарядов.
(20.5) Если r и j равны нулю, то эти уравнения упрощаются:
(20.7) Стало быть, в пустом пространстве и скалярный потенциал j, и каждая компонента векторного потенциала А удовлетворяют одному и тому же математическому уравнению. Пусть буквой y (пси) мы обозначили любую из четырех величин j, Ах, Ау, Аг; тогда нам нужно изучить общие решения уравнения
(20.8)
(20.9)
Точно так же можно переставлять и вычисление rot и d/dt:
Из этого мы получаем следующее дифференциальное уравнение
(20.10) Тем самым выясняется, что компонента магнитного поля В удовлетворяет трехмерному волновому уравнению. Подобно этому, из того факта, что Е=-Ñj-dAJdt, следует, что электрическое поле Е в пустом пространстве удовлетворяет трехмерному волновому уравнению
(20.11) Все наши электромагнитные поля подчиняются одному и тому же уравнению (20.8). Можно еще спросить: каково самое общее решение этого уравнения? Однако прежде, чем решать этот трудный вопрос, сначала посмотрим, что можно сказать в общем случае о тех решениях, в которых по у и по z ничего не меняется. (Всегда сначала беритесь за простые случаи, чтобы было видно, чего следует ожидать, а уж потом можете переходить к случаям посложней.) Предположим, что величина полей зависит только от х, так что по у и по z поля не меняются. Мы, следовательно, опять рассматриваем плоские волны и должны ожидать, что получатся те же результаты, что и в предыдущей главе. И мы действительно получим в точности те же самые ответы. Вы можете спросить: «Но зачем снова делать то же самое?» Это важно, во-первых, потому, что мы не доказали, что найденные нами волны представляют собой самое общее решение для плоских волн, и, во-вторых, потому что наши поля произошли от источника тока особого вида. Сейчас мы хотели бы выяснить такой вопрос: каков самый общий вид одномерной волны в пустом пространстве? Мы не узнаем этого, если будем рассматривать тот или иной источник особого вида, нам нужна большая общность. Кроме того, на этот раз мы будем работать не с интегральной формой уравнений, а с дифференциальной. Хотя итог одинаков, это прекрасный случай поупражняться в выкладках и убедиться в том, что не имеет значения, каким путем идти. Вы должны уметь действовать любым путем, потому что, наткнувшись на трудную задачу, вы часто обнаруживаете, что годится лишь один из многих способов расчета.
(20.12)
(20.13) Мы предположили, что по у и z поле не меняется, так что два последних члена равны нулю. Тогда, согласно (20.13),
(20.14) Решением его является постоянное в пространстве Ех (компонента электрического поля в направлении х). Взглянув на уравнение IV в (20.12) и полагая, что В тоже не изменяется вдоль y и z, вы убедитесь, что Ех постоянно и во времени. Таким полем может оказаться постоянное поле от какого-то заряженного конденсатора вдали от этого конденсатора. Нас сейчас не занимают такие неинтересные статические поля; мы интересуемся лишь динамически изменчивыми полями. А для динамических полей Ех=0. Итак, мы пришли к важному результату о том, что при распространении плоских волн в произвольном направлении электрическое поле должно располагаться поперек направления своего распространения. Конечно, у него еще остается возможность каким-то сложным образом изменяться по координате х. Поперечное поле Е можно всегда разбить на две компоненты, скажем на у и z. Так что сначала разберем случай наличия у электрического ноля только одной поперечной компоненты. Для начала возьмем электрическое поле, направленное по у, т. е. с нулевой z-компонентой. Ясно, что, решив эту задачу, мы всегда сможем разобрать и тот случай, когда электрическое поле всюду направлено по z. Общее решение можно всегда представить в виде суперпозиции двух таких полей. Какими простыми стали теперь наши уравнения! Теперь единственная ненулевая компонента электрического поля — это Еу, и все производные (кроме производных по х) тоже равны нулю. Остатки уравнений Максвелла выглядят чрезвычайно просто.
здесь x-компонента ÑXE равна нулю, потому что равны нулю производные по у и z; y-компонента тоже равна нулю: первый член потому, что все производные по z равны нулю, а второй потому, что Ez=0. Единственная не равная нулю компонента rot E — это z-компонента, она равна дЕу/дх. Полагая, что три компоненты ÑXE равны соответствующим компонентам —dB/dt, мы заключаем, что
(20.16) Поскольку временные производные как x-компоненты магнитного поля, так и y-компоненты магнитного поля равны нулю, то обе эти компоненты суть попросту постоянные поля и отвечают найденным раньше магнитостатическим решениям. Ведь кто-то мог оставить постоянный магнит возле того места, где распространяются волны. Мы будем игнорировать эти постоянные поля и положим Вх и Вy равными нулю. Кстати, о равенстве нулю x-компонент поля В мы должны были бы заключить и по другой причине. Поскольку дивергенция В равна нулю (по третьему уравнению Максвелла), то мы, прибегая при рассмотрении электрического поля к тем же доводам, что и выше, должны были бы прийти к выводу, что продольная компонента магнитного поля не может изменяться вдоль х. А раз мы такими однородными полями в наших волновых решениях пренебрегаем, то нам следовало бы положить Вх равным нулю. В плоских электромагнитных волнах поле В, равно как и поле Е, должно быть направлено поперек направления распространения самих волн. Равенство (20.16) дает нам добавочное утверждение о том, что если электрическое поле имеет только y-компоненту, то магнитное поле имеет только z-компоненту. Значит, Е и В перпендикулярны друг другу. Именно это и наблюдалось в той волне особого типа, которую мы уже рассмотрели.
Из шести производных от компонент В только dBz/dx не равна нулю. Так что три уравнения просто дают
(20.18)
(20.19) Мы уже встречали это дифференциальное уравнение, когда изучали распространение звука. Это волновое уравнение для одномерных волн. Заметьте, что в процессе вывода мы получили больше, чем содержится в (20.11). Уравнения Максвелла дали нам информацию и о том, что у электромагнитных волн есть только компоненты поля, расположенные под прямым углом к направлению распространения волн.
(20.20) то одним из возможных решений является функция ψ (x, t),
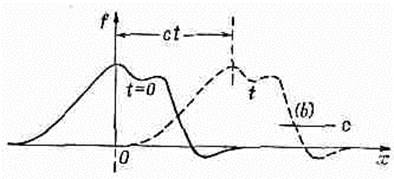
(20.21) т. е. функция одной-единственной переменной (x-ct). Функция i(x-ct) представляет собой «жесткое» образование вдоль оси х, которое движется по направлению к положительным х со скоростью с (фиг. 20.4). Так, если максимум функции f приходится на нулевое значение аргумента, то при t=0 максимум ψ оказывается при x=0. В более поздний момент, скажем при t=10, максимум ψ окажется в точке х=10 с. Когда время движется, максимум тоже движется в сторону возрастания х со скоростью с. Порой удобнее считать, что решение одномерного волнового уравнения является функцией от (t-х/с). Однако в сущности это одно и то же, потому что любая функция от (t-х/с)— это
Фиг. 20.4. Функция f(x-ct) представляет неизменный «контур», движущийся в направлении возрастания х со скоростью с.
Дифференцируя (20.21) по х, получаем
(20.22) А производные ψ no t дают
(20.23) Мы убеждаемся, что ψ действительно удовлетворяет одномерному волновому уравнению. Вы недоумеваете: «Откуда же вы взяли, что решением волнового уравнения является f(x-ct)? Мне эта проверка задним числом совсем не нравится. Нет ли прямого пути отыскать решение?» Хорошо, вот вам прямой путь: знать решение. Можно, конечно, «испечь» по всей науке прямые математические аргументы, тем более, что мы знаем, каким должно быть решение, но с таким простым, как у нас, уравнением игра не стоит свеч. Со временем вы сами дойдете до того, что, как только; увидите уравнение (20.20), тут же будете представлять себе f(x-ct)=ψв качестве решения. (Подобно тому, как сейчас при виде интеграла от x2dx у вас сразу всплывает ответ x3/3.) На самом деле вы должны представлять себе немножко больше. Решением является не только любая функция от (x-ct), но и функция от (х+сt). Из-за того, что в волновом уравнении с встречается только в виде с2, изменение знака с ничего не меняет. И действительно, самое общее решение одномерного волнового уравнения — это сумма двух произвольных функций, одной от аргумента (x-ct), а другой от (x+ct):
(20.24) Первое слагаемое дает волну, движущуюся по направлению к положительным х, второе — произвольную волну, бегущую к отрицательным х. Общее решение получается наложением двух таких волн, существующих одновременно. ● ● ● Следующий забавный вопрос решите сами. Возьмем функцию ψ в виде ψ=coskxcoskct. Эта функция не имеет вида f(x-ct) или g(x+ct). Но прямой подстановкой в (20.20) легко убедиться, что она удовлетворяет волновому уравнению. Но как же мы тогда смеем говорить, что общее решение имеет вид (20.24)? ● ● ● Применяя эти выводы о решении волнового уравнения к y-компоненте электрического поля Еу, мы заключаем, что Е может меняться по х произвольным образом. Всякое поле, которое существует в самом деле, можно всегда рассматривать как сумму двух картин. Одна волна плывет через пространство в каком-то направлении со скоростью с, причем связанное с нею магнитное поле перпендикулярно к электрическому; другая волна бежит в противоположном направлении с той же скоростью. Такие волны отвечают хорошо нам известным электромагнитным волнам — свету, радиоволнам, инфракрасному излучению, ультрафиолету, рентгеновским лучам и т. д. Мы уже изучали очень подробно излучение света. Так как все, чему мы тогда научились, применимо к любым электромагнитным волнам, то теперь нет нужды рассматривать подробно поведение этих волн. Пожалуй, стоит лишь сделать несколько замечаний о поляризации электромагнитных волн. Раньше мы решили рассмотреть частный случай электрического поля с одной только y-компонентой. Имеется, конечно, и другое решение для волн, бегущих в направлении +х или -х, т. е. решение, при котором электрическое поле обладает одной лишь z-компонентой. Так как уравнения Максвелла линейны, общее решение для одномерных волн, распространяющихся в направлении х, есть сумма волн Еy и волн Еz. Общее
(20.25) У подобных электромагнитных волн направление вектора Е не неизменно: оно как-то произвольно смещается по спирали в плоскости yz. Но в каждой точке магнитное поле всегда перпендикулярно к электрическому и к направлению распространения. Если присутствуют только волны, бегущие в одном направлении (скажем, в положительном направлении х), то имеется простое правило, говорящее об относительной ориентации электрического и магнитного полей. Правило состоит в том, что векторное произведение ЕXВ (которое, как известно, является вектором, поперечным и к Е, и к В) указывает направление, куда бежит волна. Если Е совмещать с В правым поворотом, то вектор поворота показывает направление вектора скорости волны. (Позже мы увидим, что вектор ЕXВ имеет особый физический смысл: это вектор, описывающий течение энергии в электромагнитном поле.) Трехмерные волны
(20.26)
Как же нам найти общее решение этого уравнения? Ответ таков: все решения трехмерного волнового уравнения могут быть представлены в виде суперпозиции уже найденных нами одномерных решений. Мы получили уравнение для волн, бегущих в направлении х, предположив, что поле не зависит от у и z. Конечно, имеются и другие решения, в которых поля не зависят от x и z,— это волны, идущие в направлении у. Затем существуют решения, не зависящие от х и y; они представляют волны, движущиеся в направлении z. Или в общем случае, поскольку мы записали наши уравнения в векторной форме, трехмерное волновое уравнение может иметь решения, которые являются плоскими волнами, бегущими, вообще говоря, в любом направлении. Кроме того, раз уравнения линейны, то одновременно может распространяться сколько угодно плоских волн, бегущих в каких угодно направлениях. Таким образом, самое общее решение трехмерного волнового уравнения является суперпозицией всех видов плоских волн, бегущих во всех возможных направлениях. Попытайтесь представить себе, как выглядят сейчас электрические и магнитные поля в нашей аудитории. Прежде всего здесь имеется постоянное магнитное поле; оно возникло от токов внутри нашей Земли, от постоянного земного магнетизма. Затем здесь имеются какие-то нерегулярные, почти статические электрические поля. Они скорей всего созданы электрическими зарядами, появляющимися из-за того, что кто-то ерзает на своем стуле или трется рукавами о стол (словом, в результате трения). Кроме того, здесь есть еще и другие магнитные поля, вызванные переменными токами в электропроводке,— поля, которые меняются с частотой в 50 гц в такт с работой генератора на городской электростанции. Но еще больший интерес представляют электрические и магнитные поля, меняющиеся быстрее. К примеру, там, где свет падает из окна, освещая стены и пол, имеются небольшие колебания электрического и магнитного полей, перемещающиеся за секунду на 300 000 км. По комнате еще распространяются инфракрасные волны, идущие от ваших горячих голов к холодной доске с формулами. Да! Мы еще позабыли об ультрафиолетовом свете, о рентгеновских лучах и о радиоволнах, которые проносятся по комнате. Через комнату скользят электромагнитные волны, которые несут в себе джазовую музыку. Проносятся и волны, модулированные серией импульсов, представляющих картины событий, которые происходят сейчас в других местах света, или картины воображаемых явлений, происходящих при растворении воображаемого аспирина в воображаемых желудках. Чтобы убедиться в реальности этих волн, достаточно просто включить электронную аппаратуру, которая превращает эти волны в изображения и звуки. Если мы займемся дальнейшим анализом еще более слабых колебаний, то заметим мельчайшие электромагнитные волны, пришедшие в нашу комнату с огромных расстояний. В ней существуют мельчайшие колебания электрического поля, гребни которых отстоят друг от друга примерно на фут, а источник их удален отсюда на миллионы миль. Эти волны передаются на Землю с межпланетной станции Маринер II, которая как раз проходит сейчас где-то мимо Венеры. Ее сигналы несут сводку всей той информации, которую ей удалось ухватить у планеты (информации, полученной от электромагнитных волн, дошедших от Венеры к станции). И есть здесь еще едва заметные колебания электрических и магнитных полей от волн, возникших в миллиардах световых лет отсюда, в галактиках, находящихся в удаленнейших уголках Вселенной. В том, что это действительно так, убедились, «заполнив комнату проволокой», т. е. соорудив антенны величиной с эту комнату. Так были замечены радиоволны, дошедшие до нас из мест, находящихся за пределами досягаемости крупнейших оптических телескопов. Кстати, даже эти оптические телескопы всего лишь простые собиратели электромагнитных волн. А то, что мы называем звездами, лишь заключения — заключения, выведенные из единственной физической реальности, которую мы до сих пор от них получали, из тщательного изучения бесконечно сложных волновых движений электрических и магнитных полей, достигающих Земли. В аудитории имеются, конечно, еще другие разные поля — от молний, вспыхивающих где-то вдалеке отсюда, от заряженных частиц в космических лучах в тот момент, когда они проносятся сквозь комнату, и еще поля и еще... Представляете, какая сложная штука все эти электрические поля в пространстве вокруг нас! И все они подчиняются трехмерному волновому уравнению. Научное воображение Я просил вас представить себе электрические и магнитные поля. Что вы для этого сделали? Знаете ли вы, как это нужно сделать? И как я сам представляю себе электрическое и магнитное поля? Что я на самом деле при этом вижу? Что требуется от научного воображения? Отличается ли оно чем-то от попытки представить себе комнату, полную невидимых ангелов? Нет, это не похоже на такую попытку. Чтобы получить представление об электромагнитном поле, требуется более высокая степень воображения. Почему? Да потому что для того, чтобы невидимые ангелы стали доступны пониманию, мне нужно только чуть-чуть изменить их свойства — я делаю их слегка видимыми, и тогда я уже могу увидеть и форму их крыльев, и их тела, и их нимбы. Как только мне удалось представить себе видимого ангела, то необходимая для дальнейшего абстракция (состоящая в том, чтобы почти невидимых ангелов представить себе совершенно невидимыми) оказывается сравнительно легким делом. Вы можете тоже сказать: «Профессор, дайте мне, пожалуйста, приближенное описание электромагнитных волн, пусть даже слегка неточное, но такое, чтобы я смог увидеть их так, как я могу увидеть почти невидимых ангелов. И я видоизменю эту картину до нужной абстракции». Увы, я не могу этого сделать для вас. Я просто не знаю как. У меня нет картины этого электромагнитного поля, которая была бы хоть в какой-то степени точной. Я узнал об электромагнитном поле давным-давно, 25 лет тому назад, когда я был на вашем месте, и у меня на 25 лет больше опыта размышлений об этих колеблющихся волнах. Когда я начинаю описывать магнитное поле, движущееся через пространство, то говорю о полях Е и В, делаю руками волнистые движения и вы можете подумать, что я способен их видеть. А на самом деле, что я при этом вижу? Вижу какие-то смутные, туманные, волнистые линии, на них там и сям надписано Е и В, а у других линий имеются словно какие-то стрелки, то здесь, то там на них есть стрелки, которые исчезают, едва в них вглядишься. Когда я рассказываю о полях, проносящихся сквозь пространство, в моей голове катастрофически перепутываются символы, нужные для описания объектов, и сами объекты. Я не в состоянии дать картину, хотя бы приблизительно похожую на настоящие волны. Так что, если вы сталкиваетесь с такими же затруднениями при попытках представить поле, не терзайтесь, дело обычное. Наша наука предъявляет воображению немыслимые требования. Степень воображения, которая теперь требуется в науке, несравненно превосходит то, что требовалось для некоторых прежних идей. Нынешние идеи намного труднее вообразить себе. Правда, мы используем для этого множество средств. В ход пускаются математические уравнения и правила, рисуются различные картинки. Вот сейчас я ясно осознаю, что всегда, когда я завожу речь об электромагнитном поле в пространстве, фактически перед моим взором встает своего рода суперпозиция всех тех диаграмм на эту тему, которые я когда-либо видывал. Я не воображаю себе маленьких пучков линий поля, снующих туда и сюда; они не нравятся мне потому, что если бы я двигался с иной скоростью, то они бы исчезли. Я не всегда вижу и электрические, и магнитные поля, потому что временами мне кажется, что гораздо правильнее была бы картина, включающая векторный и скалярный потенциалы, ибо последние, пожалуй, имеют больший физический смысл, чем колебания полей. Быть может, вы считаете, что остается единственная надежда на математическую точку зрения. Но что такое математическая точка зрения? С математической точки зрения в каждом месте пространства существует вектор электрического поля и вектор магнитного поля, т. е. с каждой точкой связаны шесть чисел. Способны ли вы вообразить шесть чисел, связанных с каждой точкой пространства? Это слишком трудно. А можете вы вообразить хотя бы одно число, связанное с каждой точкой пространства? Я лично не могу! Я способен себе представить такую вещь, как температура в каждой точке пространства. Но это, по-видимому, вообще вещь представимая: имеется теплота и холод, меняющиеся от места к месту. Но, честное слово, я не способен представить себе число в каждой точке. Может быть, поэтому стоит поставить вопрос так: нельзя ли представить электрическое поле в виде чего-то сходного с температурой, скажем, похожего на смещения куска студня? Сначала вообразим себе, что мир наполнен тонкой студенистой массой, а поля представляют собой какие-то искривления (скажем, растяжения или повороты) этой массы. Вот тогда можно было бы себе мысленно вообразить поле. А после того, как мы «увидели», на что оно похоже, мы можем отвлечься от студня. Именно это многие и пытались делать довольно долгое время. Максвелл, Ампер, Фарадей и другие пробовали таким способом понять электромагнетизм. (Порой они называли абстрактный студень «эфиром».) Но оказалось, что попытки вообразить электромагнитное поле подобным образом на самом деле препятствуют прогрессу. К сожалению, наши способности к абстракциям, к применению приборов для обнаружения поля, к использованию математических символов для его описания и т. д. ограниченны. Однако поля в известном смысле — вещь вполне реальная, ибо, закончив возню с математическими уравнениями (все равно, с иллюстрациями или без, с чертежами или без них, пытаясь представить поле въяве или не делая таких попыток), мы все же можем создать приборы, которые поймают сигналы с космической ракеты или обнаружат в миллиарде световых лет от нас галактику, и тому подобное. Вопрос о воображении в науке наталкивается зачастую на непонимание у людей других специальностей. Они принимаются испытывать наше воображение следующим способом. Они говорят: «Вот перед вами изображены несколько людей в некоторой ситуации. Как вы представляете, что с ними сейчас случится?» Если вы ответите: «Не могу себе представить», они могут счесть вас за человека со слабым воображением. Они проглядят при этом тот факт, что все, что допускается воображать в науке, должно согласовываться со всем прочим, что нам известно: что электрические поля и волны, о которых мы говорим, это не просто удачные мысли, которые мы вызываем в себе, если нам этого хочется, а идеи, которые обязаны согласовываться со всеми известными законами физики. Недопустимо всерьез воображать себе то, что очевидным образом противоречит известным законам природы. Так что наш род воображения — весьма трудная игра. Надо иметь достаточно воображения, чтобы думать о чем-то никогда прежде не виденном, никогда прежде не слышанном. В то же время приходится, так сказать, надевать на мысли смирительную рубашку, ограничивать их условиями, вытекающими из наших знаний о том, какому пути на самом деле следует природа. Проблема создания чего-то, что является совершенно новым и в то же время согласуется со всем, что мы видели раньше,— проблема чрезвычайно трудная. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|