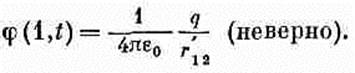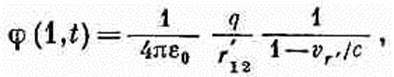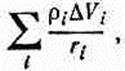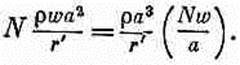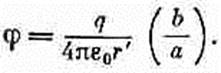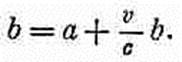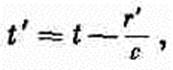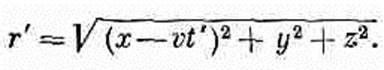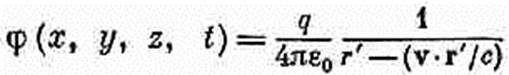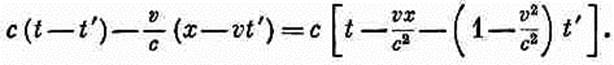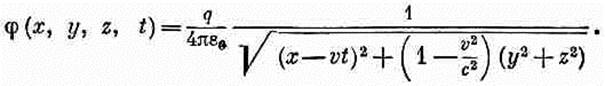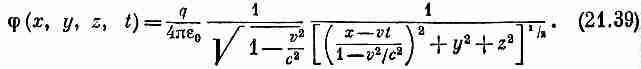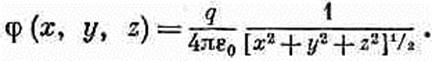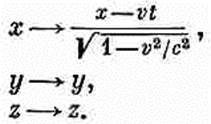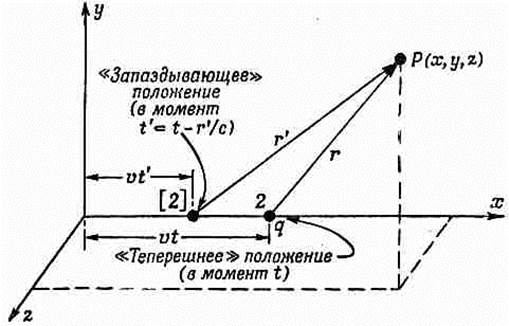
Потенциалы движущегося заряда; общее решение Льенара и Вихерта

В предыдущем параграфе мы пошли на упрощение при вы­числении интеграла для А, рассматривая только небольшие скорости. Но при этом мы шли таким путем, которым легко можно прийти и к новым выводам. Поэтому сейчас мы заново предпри­мем расчет потенциалов точечного заряда, движущегося уже, как ему захочется (даже с релятивистской скоростью). Как только мы получим этот результат, у нас в руках окажутся электромагнитные свойства электрических зарядов во всей их полноте. Даже формулу (21.1') можно будет тогда легко полу­чить, взяв только нужные производные. И наш рассказ удастся, наконец, довести до конца. Итак, запаситесь терпе­нием!

Попробуем подсчитать в точке (х₁, у₁, z₁) скалярный по­тенциал j(1), создаваемый точечным зарядом (вроде электро­на), движущимся любым, каким угодно образом. Под «точеч­ным» зарядом подразумевается очень маленький заряженный шарик, такой маленький, как только можно себе представить, с плотностью заряда р(х, у, z). Потенциал j можно найти из (21.15):

(21.28)

На первый взгляд кажется (и почти все так и подумают), что ответ состоит в том, что интеграл от r по такому «точечному» заряду равен просто общему заряду q, т. е. что

Через r'₁₂ здесь обозначен радиус-вектор от заряда в точке (2) к точке (7), измеренный в более раннее время (t—r₁₂/c). Эта формула ошибочна.

Фиг. 21.5. «Точечный» заряд (рассматриваемый как неболь­шое распределение зарядов в форме куба), движущийся со скоростью v к точке (1).

Правильный ответ такой:

(21.29)

где v_r' — компонента скорости заряда, параллельная r₁₂, т. е. направленная к точке (1). Сейчас я объясню, почему это так. Чтобы легче было следить за моими доводами, я сперва проведу расчет для «точечного» заряда в форме небольшого заряженного кубика, который движется к точке (1) со ско­ростью v(фиг. 21:5). Сторона куба будет а, это число пусть будет много меньше r₁₂ [расстояния от центра заряда до точки (1)].

Чтобы оценить величину интеграла (21.28), мы вернемся к основному определению: запишем его в виде суммы

(21.30)

где r_i — расстояние от точки (1) к i-му элементу объема DV_i, а r_i-— плотность заряда в DV_i в момент t_i=(t-r_i/с). Поскольку все r_i>>а, удобно будет выбрать все DV_i в виде тонких прямо­угольных ломтиков, перпендикулярных к r₁₂ (фиг. 21.6).

Предположим, что мы начали с того, что взяли элементы объема DV_i некоторой толщины w, много меньшей а.

Отдельные элементы объема будут выглядеть так, как по­казано на фиг. 21.7, а. Их нарисовано гораздо больше, чем нужно, чтобы закрыть весь заряд. А сам заряд не показан, и по весьма существенной причине. Где его нужно нарисовать? Ведь для каждого элемента объема DV_i надо брать r в свой момент t~(t-r/с). Но раз заряд движется, то для каждого элемента объема DV_i он окажется в другом месте!

Начнем, скажем, с элемента объема 1 на фиг. 21.7, а, выбранного так, чтобы в момент t_l = (t-r₁/с) «задняя» грань заряда пришлась на DV_i (фиг, 21.7, б).

Фиг. 21.6, Элемент объема DV_i, используемый для вычисления потенциалов.

Фиг. 21.7. Интегрирование r(t-r'/c)dV для движущегося заряда.

Тогда, вычисляя r₂DV₂, нужно взять положение заряда в несколько более позд­нее время t₂=(t- r₂/c) и заряд к этому времени сместится в по­ложение, показанное на фиг. 21.7, в. Так же будет с DV₃, DV₄ и т. д. Вот теперь можно подсчитывать сумму.

Толщина каждого DV_i- равна w, а объем wa². Поэтому каж­дый элемент объема, накладывающийся на распределение заряда, содержит в себе заряд wa²r, где r — плотность заряда внутри куба (мы считаем ее однородной). Когда расстояние от заряда до точки (1) велико, то можно все r_i в знаменателях по­ложить равными некоторому среднему значению, скажем, взятому с учетом запаздывания положению r' центра куба. Сумма (21.30) превращается в

где DV_N—тот последний элемент DV_i, который еще накла­дывается на распределение зарядов (см. фиг. 21.7, д). Сумма тем самым равна

Но ra³ — просто общий заряд q, a Nw—длина b, показанная на фиг. 21.7, д. Получается

(21.31)

А чему же равно b? Это длина куба зарядов, увеличенная на расстояние, пройденное зарядом за время от t₁=(t-r₁/с) до t_N=(t—r_N/с). Это расстояние, пройденное зарядом за время

А поскольку скорость заряда равна v, то пройденное рас­стояние равно vDt = vb/c. Но длина b — само это расстояние плюс a:

Отсюда

Здесь, конечно, под v подразумевается скорость в «запазды­вающий» момент t' = (t-r'/с); это можно указать, записав [1—v/c]_зап; тогда уравнение (21.23) для потенциала прини­мает вид

Это согласуется с тем, что было предположено в (21.29). Поя­вился поправочный множитель. Он появился потому, что в то время, как наш интеграл «проносится над зарядом», сам заряд движется. Когда заряд движется к точке (1), его вклад в ин­теграл увеличивается в b/а раз. Поэтому правильное значение интеграла равно q/r', умноженному на b/а, т.е. на 1/[1—v/c]_зan.

Если скорость заряда направлена не к точке наблюдения (1), то легко видеть, что важна только составляющая его скорости в направлении к точке (1). Если обозначить эту составляющую скорости через v_r, то поправочный множитель запишется в виде 1/[1-v_r/с]_зап. Кроме того, проделанный нами анализ в равной степени проходит для распределения заряда любой формы (это не обязательно должен быть куб). Наконец, поскольку «раз­мер» а заряда не вошел в окончательный итог, то тот же резуль­тат получится, если заряд стянется до любых размеров, вплоть до точки. Общий результат состоит в том, что скалярный потен­циал точечного заряда, движущегося с произвольной скоростью,

(21.32)

Это уравнение часто пишут в эквивалентном виде:

(21.33)

где r — вектор, соединяющий заряд с той точкой (1), в кото­рой вычисляется потенциал j, а все величины в скобках надо вычислять в «запаздывающий» момент времени t'=(t—r'/c).

То же самое получается и тогда, когда по (21.16) вычисляют А для точечного заряда. Плотность тока равна rv, а интеграл от r — тот же, что и в j. Векторный потенциал равен

(21.34)

Потенциалы точечного заряда в этой форме были впервые получены Льенаром и Вихертом. Их так и называют: потенциалы Льенара — Вихерта.

Чтобы замкнуть круг и вернуться к формуле (21.1), теперь нужно только подсчитать Е и В из этих потенциалов (при помо­щи B=ÑXA и Е=-Ñj-dA/dt). Теперь остается одна арифме­тика. Впрочем, арифметика эта довольно запутанна, так что мы не будем приводить здесь детали счета. Придется поверить мне на слово, что формула (21.1) эквивалентна выведенным нами потенциалам Льенара — Вихерта.

*Если у вас достаточно времени и вам не жаль бумаги, то попытай­тесь проделать это самостоятельно. Вот вам парочка советов: во-первых, не забывайте, что производные r' довольно запутанны, ведь они суть функции от t'! Во-вторых, не пытайтесь вывести формулу (21.1); лучше проделайте в ней все дифференцирования и затем сопоставьте то, что у вас получится, с выражением для Е, полученным из потенциалов (21.33) и (21.34).

§ 6. Потенциалы заряда, движущегося с постоянной скоростью; формула Лоренца

Применим теперь потенциалы Льенара — Вихерта к случаю заряда, движущегося по прямой с постоянной скоростью, и вычислим поле этого заряда. Позже мы повторим этот вывод, используя уже принцип относительности. Мы знаем величину потенциалов в той системе, в которой заряд покоится. Когда заряд движется, то все получается простым релятивистским преобразованием от одной системы к другой. Но теория отно­сительности ведет свое начало от теории электричества и магне­тизма. Формулы преобразований Лоренца [см. гл. 15 (вып. 2)]— это открытия, сделанные Лоренцем при исследовании уравне­ний электричества и магнетизма. И для того чтобы вы понимали, откуда все пошло, я хочу показать вам, что уравнения Максвелла действительно приводят к преобразованиям Лоренца. Я начну с вычисления потенциала равномерно движущегося заряда прямо из электродинамики, из уравнений Максвелла. Мы уже показали, что уравнения Максвелла приводят к потен­циалу, полученному в предыдущем параграфе. Стало быть, пользуясь этими потенциалами, мы используем тем самым тео­рию Максвелла.

Пусть имеется заряд, движущийся вдоль оси х со скоростью v (фиг. 21.8). Нас интересуют потенциалы в точке Р(х, у, z). Если (=0 — момент, в который заряд проходит через начало координат, то в момент t заряд окажется в точке x—vt, y=z=0. А нам нужно знать его положение с учетом запаздывания, т. е. положение в момент

(21.35)

где r' — расстояние от заряда до точки Р в этот запаздываю­щий момент. В это более раннее время t' заряд был в x=vt', так что

(21.36)

Чтобы найти r' или t', это уравнение надо сопоставить с (21.35). Исключим сперва r', решив (21.35) относительно r' и подставив в (21.36). Возвысив затем обе части в квадрат,

т. е. квадратное уравнение относительно t'. Раскрыв скобки и расположив члены по степеням t', получим

Фиг. 21.8. Определение потенциала в точке Р заряда, движущегося равномерно вдоль оси х.

Отсюда найдем

Чтобы получить r', надо это t' подставить в

Теперь мы уже можем найти j из выражения (21.33), имеющего вид

(21.38)

(ввиду того, что v постоянно).

Составляющая v в направлении r' равна v(x-vt')/r', так что v•r' просто равно v(x-vt'), а весь знаменатель равен

Подставляя (1-v²/c²)t' из (21.37), получаем

Это уравнение становится более понятным, если переписать его в виде

Векторный потенциал А — это такое же выражение, но с до­бавочным множителем v/c²:

В выражении (21.39) со всей ясностью предстает перед вами начало преобразований Лоренца. Если бы заряд находился в начале координат в своей собственной системе покоя, то его потенциал имел бы вид

А мы смотрим на него из движущейся системы координат, и нам кажется, что координаты следует преобразовать с помощью формул

Это обычное преобразование Лоренца. Лоренц вывел его тем же самым способом, каким пользовались и мы.

Но что можно сказать о добавочном множителе 1/Ö(1-v²/с²), который появился перед дробью в (21.39)? И кроме того, как появляется векторный потенциал А, если он в системе покоя частицы повсюду равен нулю? Мы вскоре покажем, что А и j вместе составляют четырехвектор, подобно импульсу р и полной энергии U частицы. Добавка 1/Ö(1—v²/c²) в (21.39)—это тот самый множитель, который появляется всегда, когда пре­образуют компоненты четырехвектора, так же как плотность заряда r преобразуется в r/Ö(1-v²/c²). Собственно из формул (21.4) и (21.5) почти очевидно, что А и j суть компоненты одного четырехвектора, потому что в гл. 13 (вып. 5) уже было пока­зано, что j и r — компоненты четырехвектора.

Позднее мы более подробно разберем относительность в электродинамике; здесь мы хотели только показать, как естест­венно уравнения Максвелла приводят к преобразованиям Лоренца. Поэтому не надо удивляться, узнав, что законы электричества и магнетизма уже вполне пригодны и для теории относительности Эйнштейна. Их не нужно даже как-то особо подгонять, как это приходилось делать с ньютоновой механи­кой.

* С обратным знаком. См. дальше.— Прим. ред.

*Формула была выведена Р. Фейнманом в 1950 г. и приводится иног­да в лекциях как удобный способ расчета синхротронного излучения.

ЦЕПИ ПЕРЕМЕННОГО ТОКА

Импедансы

Генераторы

Не нашли, что искали? Воспользуйтесь поиском по сайту: