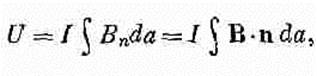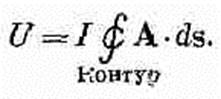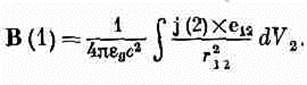|
|
Механическая и электрическая энергииТеперь мы хотим пояснить, почему энергия Uмех, о которой говорилось в предыдущем параграфе, не настоящая энергия, связанная с постоянными токами, почему у нее нет прямой связи с полной энергией всей Вселенной. Правда, мы подчеркнули, что ею можно пользоваться как энергией, когда вычисляешь силы из принципа виртуальной работы, при условии, что ток в петле (и все прочие токи) не меняется. Посмотрим теперь, почему же все так выходит. Представим, что петля на фиг. 15.2 движется в направлении +х, а ось z примем за направление В. Электроны проводимости на стороне 2 будут испытывать действие силы, толкающей их вдоль провода, в направлении у. Но в результате их движения по проводу течет электрический ток и имеется составляющая скорости vy в том же направлении, в котором действует сила. Поэтому над каждым электроном каждую секунду будет производиться работа Fyvy , где vy — компонента скорости электрона, направленная вдоль провода. Эту работу, совершаемую над электронами, мы назовем электрической. Оказывается, что когда петля движется в однородном поле, то полная электрическая работа равна нулю, потому что на одной части петли работа положительная, а на другой — равная ей отрицательная. Но при движении контура в неоднородном поле это не так — тогда остается какой-то чистый избыток одной работы над другой. Вообще-то эта работа стремится изменить поток электронов, но если он поддерживается неизменным, то энергия поглощается или высвобождается в батарейке или в другом источнике, сохраняющем ток постоянным. Вот именно эта энергия и не учитывалась, когда мы вычисляли Uмех в (15.9), потому что в наши расчеты входили только механические силы, действующие на провод. Вы можете подумать: но сила, действующая на электроны, зависит от того, насколько быстро движется провод; быть может, если бы провод двигался достаточно медленно, этой электрической энергией можно было бы вообще пренебречь. Действительно, скорость, с какой высвобождается электрическая энергия, пропорциональна скорости провода, но все же полная выделенная энергия пропорциональна к тому же еще и времени, в течение которого проявлялась эта скорость. В итоге полная выделенная электрическая энергия пропорциональна произведению скорости на время, а это как раз и есть пройденное расстояние. Каждому пройденному в поле расстоянию отвечает заданное, и притом одно и то же, количество электрической работы.
И поскольку ток поддерживается неизменным, то силы, действующие на электроны проводимости, не ускоряют их; электрическая энергия переходит не к электронам, а к тому источнику, который сохраняет силу тока постоянной. Но заметьте, что сила, действующая на провод, равна IB; значит, IBvпровод — это механическая работа, выполняемая над проводом в единицу времени, dUмех/dt = IBvпровод. Отсюда мы заключаем, что механическая работа перемещения провода в точности равна электрической работе, производимой над источником тока, так что энергия петли остается постоянной! Это не случайность. Это следствие закона, с которым мы уже знакомы. Полная сила, действующая на каждый из зарядов в проводе, равна
Скорость, с которой производится работа, равна
(15.12) Если электрического поля нет, то остается только второе слагаемое, а оно всегда равно нулю. Позже мы увидим, что изменение магнитных полей создает электрические поля, так что наши рассуждения применимы лишь к проводам в постоянных магнитных полях. Но тогда почему же принцип виртуальной работы дает правильный ответ? Потому, что пока мы не учитывали полную энергию Вселенной. Мы не включали в рассмотрение энергию тех токов, которые создают магнитное поле, с самого начала присутствующее в наших рассуждениях. Но представим себе полную систему, наподобие изображенной на фиг. 15.3,а, где петля с током I вдвигается в магнитное поле B1созданное током I2 в катушке. ТокI1, текущий по петле, тоже будет создавать какое-то магнитное поле В2 близ катушки. Если петля движется, то поле В2изменяется. В следующей главе мы увидим, что изменяющееся магнитное поле создает поле Е, и это поле действительно начнет действовать на заряды в катушке. Эту энергию мы обязаны включить в наш сводный баланс энергий. Мы, конечно, могли бы подождать говорить об этом новом вкладе в энергию до следующей главы, но уже сейчас можно оценить его, если применить соображения принципа относительности.
Фиг. 15.3. Вычисление энергии маленькой петли в магнитном поле.
Теперь предположим, что мы смотрим на происходящее с другой точки зрения: будем считать, что петля покоится, а катушка приближается к ней. Тогда катушка движется в поле, созданном петлей. Те же рассуждения приведут к выражению
Механическая энергия в обоих случаях одна и та же — она определяется только силой, действующей между двумя контурами. Сложение двух уравнений дает
Полная энергия всей системы равна, конечно, сумме двух электрических энергий и взятой один раз механической энергии. В итоге выходит
(15.14) А теперь предположим, что нам надо было бы подсчитать работу, затрачиваемую на сближение двух проводников, но при другом условии — что напряжение между ними остается постоянным. Тогда правильную величину силы мы могли бы получить из принципа виртуальной работы, если бы поступили немного искусственным образом. Раз Q = CV, то полная энергия равна 1/2 CV2. Но если бы мы ввели условную энергию, равную —1/2CV2, то принцип виртуальной работы можно было бы применить для получения сил, полагая изменение этой условной энергии равным механической работе (это при условии, что напряжение V
(15.15) а это то же самое, что написано в уравнении (15.14). Мы получаем правильный ответ, хотя пренебрегаем работой, которую электрическая система тратит на постоянное поддержание напряжения. И здесь опять электрическая энергия ровно вдвое больше механической и имеет обратный знак. Итак, если мы ведем расчет искусственно, пренебрегая тем фактом, что источник потенциала должен тратить работу на то, чтобы напряжение оставалось неизменным, то все равно мы приходим к правильному результату. Это в точности соответствует положению дел в магнитостатике. Энергия постоянных токов Зная, что Uполн = -Uмех, используем этот факт, чтобы найти истинную энергию постоянных токов в магнитных полях. Начать можно с истинной энергии небольшой токовой петельки. Обозначая Uполн просто через U, напишем U = m•В.(15.16) Хотя эту энергию мы подсчитали только для плоской прямоугольной петли, все это верно и для плоской петельки произвольной формы. Энергию контура произвольной формы можно найти, представив себе, что он состоит из небольших токовых петель. Скажем, имеется провод в форме петли Г (фиг. 15.4). Натянем на эту петлю поверхность S, а на ней наметим множество петелек, каждую из которых можно считать плоской. Если заставить ток I циркулировать по каждой петельке, то в итоге выйдет то же самое, как если бы ток шел только по петле Г, ибо токи на всех внутренних линиях взаимно уничтожатся. Система небольших токов физически не будет отличима от исходного контура, и энергия должна быть той же, т. е. должна быть равна сумме энергий всех петелек. Если площадь каждой петельки Dа, то ее энергия равна IDаBn, где Bn — компонента В, нормальная к Dа. Полная энергия равна U = SIBnDа.
Фиг. 15.4. Энергию большой петли в магнитном поле можно считать суммой энергий маленьких петелек.
(15.17) где n — единичная нормаль к da,
(15.18)
(15.19) В этом выражении А обозначает, конечно, векторный потенциал, возникающий из-за токов (отличных от тока / в проводе), которые создают поле В близ провода.
(15.20) Это соответствует полученному для электростатической энергии выражению
(15.21) Значит, мы можем считать А, если угодно, своего рода потенциальной энергией токов в магнитостатике. К сожалению, это представление не очень полезно, потому что оно годится только для статических полей. В действительности, если поля со временем меняются, ни выражение (15.20), ни выражение (15.21) не дают правильной величины энергии. B или А? В этом параграфе нам хотелось бы обсудить такой вопрос: что такое векторный потенциал — просто полезное для расчетов приспособление (так в электродинамике полезен скалярный потенциал) или же он как поле вполне «реален»? Или же «реально» лишь магнитное поле, так как только оно ответственно за силу, действующую на движущуюся частицу? Для начала нужно сказать, что выражение «реальное поле» реального смысла не имеет. Во-первых, вы вряд ли вообще полагаете, что магнитное поле хоть в какой-то степени «реально», потому что и сама идея поля — вещь довольно отвлеченная. Вы не можете протянуть руку и пощупать это магнитное поле. Кроме того, величина магнитного поля тоже не очень определенна; выбором подходящей подвижной системы координат можно, к примеру, добиться, чтобы магнитное поле в данной точке вообще пропало. Под «реальным» полем мы понимаем здесь вот что: реальное поле — это математическая функция, которая используется нами, чтобы избежать представления о дальнодействии. Если в точке Р имеется заряженная частица, то на нее оказывают влияние другие заряды, расположенные на каком-то удалении от Р. Один прием, которым можно описать взаимодействие,— это говорить, что прочие заряды создают какие-то «условия» (какие — не имеет значения) в окрестности Р. Если мы знаем эти условия (мы их описываем, задавая электрическое и магнитное поля), то можем полностью определить поведение частицы, нимало не заботясь после о том, что именно создало эти условия. Иными словами, если бы эти прочие заряды каким-то образом изменились, а условия в Р, описываемые электрическим и магнитным полем в точке Р, остались бы прежними, то движение заряда тоже не изменилось бы. «Реальное» поле тогда есть совокупность чисел, заданных так, что то, что происходит в некоторой точке, зависит только от чисел в этой точке и нам больше не нужно знать, что происходит в других местах. Именно с таких позиций мы и хотим выяснить, является ли векторный потенциал «реальным» полем. Вас может удивить тот факт, что векторный потенциал определяется не единственным образом, что его можно изменить, добавив к нему градиент любого скаляра, а силы, действующие на частицы, не изменятся. Однако это не имеет ничего общего с вопросом реальности в том смысле, о котором мы говорили, К примеру, магнитное поле как-то меняется при изменении относительного движения (равно как и Е или А). Но нас нисколько не будет заботить, что поле можно изменять таким образом. Нам это безразлично; это никак не связано с вопросом о том, действительно ли векторный потенциал—«реальное» поле, пригодное для описания магнитных эффектов, или же это просто удобный математический прием. Мы должны еще сделать кое-какие замечания о полезности векторного потенциала А. Мы видели, что им можно пользоваться в формальной процедуре расчета магнитных полей заданных токов, в точности как j может применяться для отыскания электрических полей. В электростатике мы видели, что j давалось скалярным интегралом
(15.22)
(15.23) Во-первых, их три, а во-вторых, каждый из них вообще-то немного посложнее, чем (15.22). В магнитостатике преимущества не так ясны. Интеграл для А уже сам по себе векторный:
(15.24)
(15.25) В простых задачах векторным потенциалом часто бывает пользоваться труднее, и вот по какой причине. Предположим, нас интересует магнитное поле В в одной только точке, а задача обладает какой-то красивой симметрией. Скажем, нам нужно знать поле в точке на оси кольцевого тока. Вследствие симметрии интеграл в (15.25) легко возьмется и вы сразу получите В. Если бы, однако, мы начали с А, то пришлось бы вычислять В из производных А, а для этого надо было бы знать А во всех точках по соседству с той,которая нас интересует. Большая же часть их не лежит на оси симметрии, интеграл для А усложняется. В задаче с кольцом, например, пришлось бы иметь дело с эллиптическими интегралами. В подобных задачах А, разумеется, не приносит большой пользы. Во многих сложных задачах, бесспорно, легче работать с А, но в общем трудно было бы доказывать, что эти технические облегчения стоят того, чтобы начать изучать еще одно векторное поле. Мы ввели А потому, что оно действительно имеет большое физическое значение. Оно не просто связано с энергиями токов (в чем мы убедились в последнем параграфе), оно — «реальное» физическое поле в том смысле, о котором мы говорили выше. В классической механике силу, действующую на частицу, очевидно, можно записать в виде F = q(E+vXB), (15.26) так что, как только заданы силы, движение оказывается полностью определенным. В любой области, где В = 0, хотя бы А и не было равно нулю (например, вне соленоида), влияние А ни в чем не сказывается. Поэтому долгое время считалось, что А — не «реальное» поле. Оказывается, однако, что в квантовой механике существуют явления, свидетельствующие о том, что поле А на самом деле вполне «реальное» поле, в том смысле, в каком мы определили это слово. В следующем параграфе мы покажем, что все это значит. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|