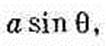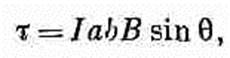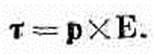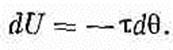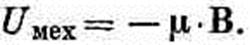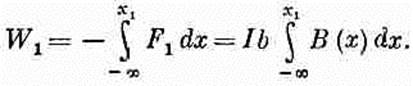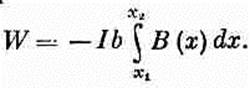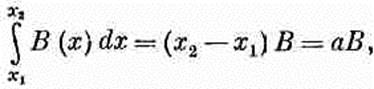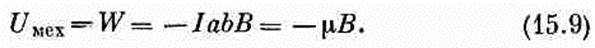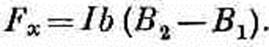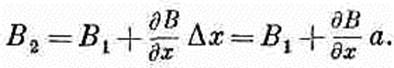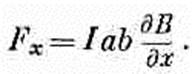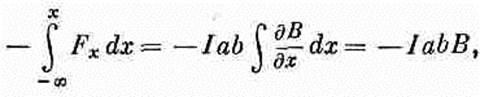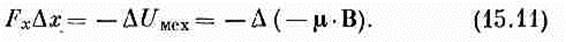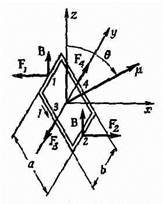
Силы, действующие на петлю с током; энергия диполя

Глава 15

ВЕКТОРНЫЙ ПОТЕНЦИАЛ

Силы, действующие на петлю с током; энергия диполя

Механическая и электрическая энергии

Энергия постоянных токов

В или А?

Векторный потенциал и квантовая механика

§ 6. Что истинно в статике, но ложно в динами­ке?

Силы, действующие на петлю с током; энергия диполя

В предыдущей главе мы изучали магнитное поле, создаваемое маленькой прямоугольной петлей, по которой течет ток. Мы нашли, что это поле диполя с дипольным моментом, равным

m= IA,(15.1)

где I — сила тока, a A — площадь петли. Момент направлен по нормали к плоскости петли, так что можно писать и так:

m=IАn,

где n — единичный вектор нормали к пло­щади А.

Петли с током, или магнитные диполи, не только создают магнитные поля, но и сами подвергаются действию силы, попав в магнит­ное поле других токов. Рассмотрим сперва силы, действующие на прямоугольную петлю в однородном магнитном поле. Пусть ось z направлена по полю, а ось y лежит в плоскости петли, образующей с плоскостью xyугол q (фиг. 15.1). Тогда магнитный момент петли, будучи нормальным к ее плоскости, образует с магнитным полем тоже угол q.

Раз токи на противоположных сторонах петли текут в противоположные стороны, то и силы, действующие на них, тоже направлены врозь, а суммарная сила равна нулю (в одно­родном поле). Но благодаря силам, действую­щим на стороны, обозначенные на фиг. 15.1 цифрами 1 и 2, возникает вращательный момент, стремящийся вращать петлю вокруг оси у. Величина этих сил F_l и F₂ такова:

F₁=F₂=IBb.

Фиг. 15.1. Прямоугольная петля с током I в однородном поле В, направленном по оси z.

Действующий на нее вращательный момент равен t=mXB, где магнитный момент m=Iab.

Их плечо равно

так что вращательный момент

Вращательный момент может быть записан и векторно:

(15.2)

То, что вращательный момент дается уравнением (15.2), мы показали пока только для довольно частного случая. Но ре­зультат, как мы увидим, верен для маленьких петель любой формы. Полезно напомнить, что и для вращательного момента, действующего на электрический диполь, мы получили соотно­шение подобного же рода:

Сейчас нас интересует механическая энергия нашей петли, по которой течет ток. Раз есть момент вращения, то энергия, естественно, зависит от ориентации петли. Принцип виртуаль­ной же работы утверждает, что момент вращения — это ско­рость изменения энергии с углом, так что можно написать

Подставляя t =+mBsinq и интегрируя, мы вправе принять за энергию выражение

(Знак минус стоит потому, что петля стремится развернуть свой момент по полю; энергия ниже всего тогда, когда m и В параллельны.)

По причинам, о которых мы поговорим позже, эта энергия не есть полная энергия петли с током. (Мы, к примеру, не учли энергии, идущей на поддержание тока в петле.) По­этому мы будем называть ее U_мех, чтобы не забыть, что это лишь часть энергии. И, кроме того, постоянную интегриро­вания в (15.3) мы вправе принять равной нулю, все равно ведь какие-то другие виды энергии мы не учли. Так что мы перепишем уравнение так:

(15.4)

Опять получилось соответствие с электрическим диполем, где было

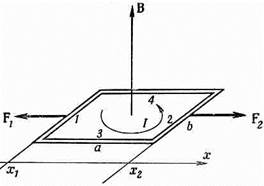
(15.5)

Только в (15.5) электрическая энергия — и вправду энергия, а U_мех в (15.4) — не настоящая энергия. Но все равно ее можно применять для расчета сил по принципу виртуальной работы. Надо только предполагать, что ток в петле (или по крайней мере магнитный момент m) остается неизменным при повороте.

Для нашей прямоугольной петли можно показать, что U_мех соответствует также работе, затрачиваемой на то, чтобы внести петлю в поле. Полная сила, действующая на петлю, равна нулю лишь в однородном поле, а в неоднородном все равно останутся какие-то силы, действующие на токовую петлю. Внося петлю в поле, мы вынуждены будем пронести ее через места, где поле неоднородно, и там будет затрачена работа. Будем считать для упрощения, что петлю вносят в поле так, что ее момент направлен вдоль поля. (А в конце, уже в поле, ее можно повер­нуть как надо.)

Вообразите, что мы хотим двигать петлю в направлении x, т. е. в ту область, где поле сильнее, и что петля ориентирована так, как показано на фиг. 15.2. Мы отправимся оттуда, где поле равно нулю, и будем интегрировать силу по расстоянию по мере того, как петля входит в поле.

Фиг. 15.2. Петлю проносят через поле В (поперек него) в направлении x.

Рассчитаем сначала работу переноса каждой стороны по отдельности, а затем все сложим (вместо того, чтобы складывать силы до интегрирования). Силы, действующие на стороны 3 и 4, направлены поперек движения, так что на эти стороны работа не тратится. Сила, действующая на сторону 2, направлена по xи равна 1bВ(x); чтобы узнать всю работу против действия магнитных сил, нужно проинтегрировать это выражение по xот некоторого значения х, где поле равно нулю, скажем, от х = -¥ до теперешнего положения х₂:

(15.6)

Подобно этому, и работа против сил, действующих на сторону 1,равна

(15.7)

Чтобы вычислить каждый интеграл, надо знать, как В(х) зависит от х. Но ведь сторона 1при движении рамки распо­ложена все время параллельно стороне 2на одном и том же расстоянии от нее, так что в ее интеграл входит почти вся работа, затраченная на перемещение стороны 2. Сумма (15.6) и (15.7) на самом деле равна

(15.8)

Но, попав в область, где В на обеих сторонах 1 и 2 почти оди­наково, мы имеем право записать интеграл в виде

где В — поле в центре петли. Вся вложенная механическая энергия оказывается равной

Это согласуется с выражением для энергии (15.4), выбранным нами прежде.

Конечно, тот же вывод получился бы, если бы мы до инте­грирования сложили все силы, действующие на петлю. Если бы мы обозначили через В₁ поле у стороны 1 а через В₂ — поле у стороны 2, то вся сила, действующая в направлении х, оказа­лась бы равной

Если петля «узкая», т. е. если В₂ и В₁ не очень различаются между собой, то можно было бы написать

Так что сила была бы равна

(15.10)

Вся работа, произведенная внешними силами над петлей, рав­нялась бы

а это опять -mВ. Но теперь нам становится понятно, почему получается, что сила, действующая на небольшую токовую петлю, пропорциональна производной магнитного поля, как это следовало ожидать из

Другой наш результат состоит в следующем. Хоть и не исклю­чено, что не все виды энергии вошли в формулу U_мех= m•B (ведь это просто некоторая имитация энергии), ею все же можно пользоваться, применяя принцип виртуальной работы, чтобы узнать, какие силы действуют на петли с постоянным током.

Не нашли, что искали? Воспользуйтесь поиском по сайту: