Предел монотонной последовательности. Определение
Числа e
Содержание
4.1. Определение монотонной последовательности. 32
4.2. Предел монотонной последовательности. 33
4.3. Определение числа  . 34 . 34
4.4. Упражнения для самостоятельной работы.. 36
Определение монотонной последовательности
Числовая последовательность  называется монотонной, если она является монотонно возрастающей или монотонно убывающей. называется монотонной, если она является монотонно возрастающей или монотонно убывающей.
 называется монотонно возрастающей последовательностью (строго возрастающей), если выполняется неравенство xn+1> xn для называется монотонно возрастающей последовательностью (строго возрастающей), если выполняется неравенство xn+1> xn для  . .
 называется монотонно убывающей последовательностью (строго убывающей), если выполняется неравенство называется монотонно убывающей последовательностью (строго убывающей), если выполняется неравенство  для для  . .
 называется монотонной последовательностью в обобщенном смысле, если определяющие неравенства являются нестрогими: называется монотонной последовательностью в обобщенном смысле, если определяющие неравенства являются нестрогими:
 - неубывающая или нестрого возрастающая; - неубывающая или нестрого возрастающая;
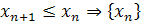 - невозрастающая или нестрого убывающая. - невозрастающая или нестрого убывающая.
Например,
1) если  , то , то  монотонно возрастает, или строго возрастает, обозначают монотонно возрастает, или строго возрастает, обозначают  ; ;
2) если  , то , то  монотонно убывает, или строго убывает, обозначают монотонно убывает, или строго убывает, обозначают  ; ;
3) последовательность с  не является монотонной; не является монотонной;
4) последовательность  нестрого возрастает, или не убывает, или возрастает в обобщенном смысле. нестрого возрастает, или не убывает, или возрастает в обобщенном смысле.
Предел монотонной последовательности
| Теорема Вейерштрасса о пределе монотонной последовательности
| 1. Всякая монотонно возрастающая последовательность  имеет предел: конечный, если она ограничена сверху, или бесконечный, если она не является ограниченной сверху; при этом имеет предел: конечный, если она ограничена сверху, или бесконечный, если она не является ограниченной сверху; при этом  .
2. Всякая монотонно убывающая последовательность имеет предел: конечный, если она ограничена снизу, или бесконечный, если она не является ограниченной снизу; при этом .
2. Всякая монотонно убывающая последовательность имеет предел: конечный, если она ограничена снизу, или бесконечный, если она не является ограниченной снизу; при этом  . .
|
w Пусть  и и  . Проведем доказательство первой части теоремы. . Проведем доказательство первой части теоремы.
Возьмём произвольную окрестность  точки точки  и обозначим через и обозначим через  её левый конец, (рис. 19 а), б)): её левый конец, (рис. 19 а), б)):
 
Рис. 19
Очевидно, что  . Из определения точной верхней грани множества имеем: . Из определения точной верхней грани множества имеем:

Так как  , то все , то все  при при  , то есть все , то есть все  , начиная с номера , начиная с номера  . Но промежуток . Но промежуток  входит в входит в 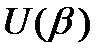 , поэтому все , поэтому все  при при  . .
По определению предела это и означает, что  . .
Вторую часть теоремы рекомендуется доказать самостоятельно аналогичным образом. v
Из теоремы Вейерштрасса следует, что монотонность числовой последовательности является достаточным условием для существования её предела (конечного, если последовательность ограниченная или бесконечного, если последовательность неограниченная). Однако это достаточное условие не является необходимым.
Например, последовательность  имеет пределом число 0, но не является монотонной. имеет пределом число 0, но не является монотонной.
Если последовательность  является и монотонной и ограниченной, то это является достаточным условием её сходимости: является и монотонной и ограниченной, то это является достаточным условием её сходимости:
 . .
Примеры (доказательство сходимости предела монотонной ограниченной последовательности)
1)  ; ;
2)  ; ;
3)  ; ;
4)  ; ;
5) 
и  ограничена снизу, например, числом 0, поэтому ограничена снизу, например, числом 0, поэтому  конечный конечный  ; ;
6)  , ,  , ,  , ,  ,… ,…  ; ограниченность этой последовательности сверху определятся следующими неравенствами: ; ограниченность этой последовательности сверху определятся следующими неравенствами:
  
 поэтому существует конечный поэтому существует конечный  . .
4.3. Определение числа 
Теорема Вейерштрасса, гарантирующая сходимость монотонной и ограниченной последовательности, используется, например, в определении числа  , имеющего широкое использование в естествознании. , имеющего широкое использование в естествознании.
Рассмотрим последовательность  , в которой: , в которой:

Докажем, что эта последовательность является монотонно возрастающей и ограниченной сверху. Для этого используем известную формулу бинома Ньютона, для натуральной степени двучлена:

полагая здесь  , ,  , получим представление для величин , получим представление для величин  : :


вынесем из каждой скобки числителя множитель  и сократим дроби на и сократим дроби на  : :

 . ( . (  ) )
Теперь видно, что все слагаемые в правой части равенства  положительны и их количество увеличивается с увеличением числа положительны и их количество увеличивается с увеличением числа  , поэтому последовательность , поэтому последовательность  монотонно возрастающая; при этом очевидна её ограниченность снизу монотонно возрастающая; при этом очевидна её ограниченность снизу  . .
Чтобы показать ограниченность этой последовательности сверху, в равенстве (  ) заменим каждую скобку на число 1; в результате правая часть равенства увеличивается и получается следующее неравенство: ) заменим каждую скобку на число 1; в результате правая часть равенства увеличивается и получается следующее неравенство:
 ; ;
ещё усилим это неравенство, заменив числа 3,4,5,…, n, стоящие в знаменателях дробей, числом 2:
 ; ;
сумму в скобке найдём по известной формуле для суммы n первых членов геометрической прогрессии со знаменателем  и тоже оценим её сверху: и тоже оценим её сверху:
 ; ;
подставив эту оценку в предыдущее неравенство, получим ограниченность сверху всех членов рассматриваемой последовательности:
  . .
Таким образом, показано, что последовательность  является монотонно возрастающей и ограниченной сверху. Следовательно, по теореме Вейерштрасса она имеет конечный предел, который обозначается числом является монотонно возрастающей и ограниченной сверху. Следовательно, по теореме Вейерштрасса она имеет конечный предел, который обозначается числом  : :
Число  называется неперовым числом. Оно принято за основание натуральных логарифмов: называется неперовым числом. Оно принято за основание натуральных логарифмов: 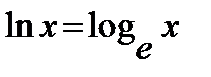 и за основание показательной функции и за основание показательной функции  , которая называется экспонентой. Мы имеем некоторую информацию об этом числе из ограниченности последовательности , которая называется экспонентой. Мы имеем некоторую информацию об этом числе из ограниченности последовательности  сверху и снизу, используя далее свойства о переходе к пределу в неравенствах и о пределе постоянной: сверху и снизу, используя далее свойства о переходе к пределу в неравенствах и о пределе постоянной:

В более подробных курсах математического анализа доказывается, что число  является иррациональным и имеет приближенное значение: является иррациональным и имеет приближенное значение: 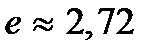 ( (  ). ).
4.4. Упражнения для самостоятельной работы
1. Докажите, используя теорему Вейерштрасса, что
1)  существует; 2) существует; 2)  ; 3) ; 3)  ; ;
4)  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|




 . 34
. 34 называется монотонной, если она является монотонно возрастающей или монотонно убывающей.
называется монотонной, если она является монотонно возрастающей или монотонно убывающей. .
. для
для  - неубывающая или нестрого возрастающая;
- неубывающая или нестрого возрастающая;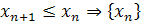 - невозрастающая или нестрого убывающая.
- невозрастающая или нестрого убывающая. , то
, то  монотонно возрастает, или строго возрастает, обозначают
монотонно возрастает, или строго возрастает, обозначают  ;
; , то
, то  монотонно убывает, или строго убывает, обозначают
монотонно убывает, или строго убывает, обозначают  ;
; не является монотонной;
не является монотонной; нестрого возрастает, или не убывает, или возрастает в обобщенном смысле.
нестрого возрастает, или не убывает, или возрастает в обобщенном смысле. .
2. Всякая монотонно убывающая последовательность имеет предел: конечный, если она ограничена снизу, или бесконечный, если она не является ограниченной снизу; при этом
.
2. Всякая монотонно убывающая последовательность имеет предел: конечный, если она ограничена снизу, или бесконечный, если она не является ограниченной снизу; при этом  .
.
 . Проведем доказательство первой части теоремы.
. Проведем доказательство первой части теоремы. точки
точки  и обозначим через
и обозначим через  её левый конец, (рис. 19 а), б)):
её левый конец, (рис. 19 а), б)): . Из определения точной верхней грани множества имеем:
. Из определения точной верхней грани множества имеем:
 , то все
, то все  при
при  , то есть все
, то есть все  , начиная с номера
, начиная с номера  . Но промежуток
. Но промежуток  входит в
входит в 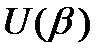 , поэтому все
, поэтому все  при
при  .
. имеет пределом число 0, но не является монотонной.
имеет пределом число 0, но не является монотонной. является и монотонной и ограниченной, то это является достаточным условием её сходимости:
является и монотонной и ограниченной, то это является достаточным условием её сходимости: .
. ;
; ;
; ;
; ;
;
 конечный
конечный  ;
; ,
,  ,
,  ,
,  ,…
,…  ; ограниченность этой последовательности сверху определятся следующими неравенствами:
; ограниченность этой последовательности сверху определятся следующими неравенствами:


 поэтому существует конечный
поэтому существует конечный  .
.
 , имеющего широкое использование в естествознании.
, имеющего широкое использование в естествознании.

 ,
,  , получим представление для величин
, получим представление для величин  :
:

 и сократим дроби на
и сократим дроби на  :
:
 . (
. (  )
) положительны и их количество увеличивается с увеличением числа
положительны и их количество увеличивается с увеличением числа  монотонно возрастающая; при этом очевидна её ограниченность снизу
монотонно возрастающая; при этом очевидна её ограниченность снизу  .
. ;
; ;
; и тоже оценим её сверху:
и тоже оценим её сверху: ;
;
 .
. :
:
 называется неперовым числом. Оно принято за основание натуральных логарифмов:
называется неперовым числом. Оно принято за основание натуральных логарифмов: 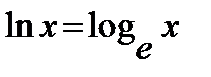 и за основание показательной функции
и за основание показательной функции  , которая называется экспонентой. Мы имеем некоторую информацию об этом числе из ограниченности последовательности
, которая называется экспонентой. Мы имеем некоторую информацию об этом числе из ограниченности последовательности  сверху и снизу, используя далее свойства о переходе к пределу в неравенствах и о пределе постоянной:
сверху и снизу, используя далее свойства о переходе к пределу в неравенствах и о пределе постоянной:
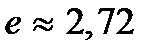 (
(  ).
). существует; 2)
существует; 2)  ; 3)
; 3)  ;
; .
.