Определение сходящейся, расходящейся, бесконечно большой или бесконечно малой последовательности
Если последовательность  имеет конечный предел: имеет конечный предел:  , то , то 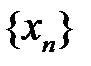 называется сходящейся последовательностью; в противном случае называется сходящейся последовательностью; в противном случае 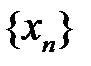 называется расходящейся последовательностью, то есть для расходящейся последовательности предел равен называется расходящейся последовательностью, то есть для расходящейся последовательности предел равен  или или 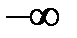 или или  или не существует. или не существует.
Если 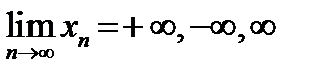 , то , то  называется бесконечно большой последовательностью. называется бесконечно большой последовательностью.
Если  , то , то  называется бесконечно малой последовательностью. называется бесконечно малой последовательностью.
Например, в рассмотренных выше примерах сходящимися являются последовательности с  , ,  а также последовательность а также последовательность  ; все эти последовательности являются также бесконечно малыми, потому что все они имеют пределом число 0. ; все эти последовательности являются также бесконечно малыми, потому что все они имеют пределом число 0.
Последовательности с  , ,  , а также последовательность , а также последовательность  являются расходящимися; из них бесконечно большой является только последовательность с общим членом являются расходящимися; из них бесконечно большой является только последовательность с общим членом  . .
1.5. Упражнения для самостоятельной работы
1. Для нескольких последовательностей известны формулы общего члена:
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; 5) ; 5)  ; ;
6) 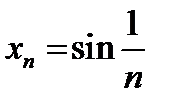 ; 7) ; 7)  ; 8) ; 8)  ; 9) ; 9) 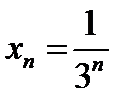 ; 10) ; 10)  . .
Для каждой из этих последовательностей вычислите несколько первых членов и по расположению чисел 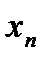 на координатной оси сделайте вывод о пределе на координатной оси сделайте вывод о пределе  . .
2. Среди последовательностей  предыдущего задания укажите номера сходящихся, расходящихся, бесконечно больших и бесконечно малых последовательностей. предыдущего задания укажите номера сходящихся, расходящихся, бесконечно больших и бесконечно малых последовательностей.
3. Докажите строго по определению предела, что:
1)  ; 2) ; 2)  ; 3) ; 3)  . .
Ответы к упражнениям для самостоятельной работы
1. 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; ;
5) 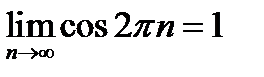 ; 6) ; 6)  ; 7) ; 7) 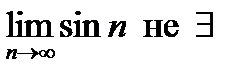 ; 8) ; 8) 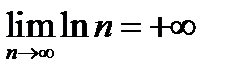 ; ;
9)  ; 10) ; 10)  . .
2. Номера сходящихся последовательностей: 1), 3), 5), 6), 9), 10);
расходящихся последовательностей: 2), 4), 7), 8);
бесконечно больших последовательностей: 2), 8);
бесконечно малых последовательностей: 1), 6), 9), 10).
Основные свойства предела последовательности. Ограниченные последовательности
Содержание
2.1. Единственность предела. 14
2.2. Предел стационарной последовательности. 15
2.3. Переход к пределу в равенстве. 15
2.4. Переход к пределу в неравенствах. 16
2.5. Теорема о зажатой последовательности. 16
2.6. Связь сходящейся последовательности с её пределом и бесконечно малой последовательностью 17
2.7. Ограниченность последовательности, связь с пределом.. 18
2.8. Упражнения для самостоятельной работы.. 21
Единственность предела
| Теорема о единственности предела
| Если существует предел последовательности  , то этот предел является единственным , то этот предел является единственным
|
w Проведем доказательство от противного. Предположим, что последовательность  имеет два различных предела: имеет два различных предела: 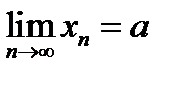 и и  . .
У двух различных точек а и b координатной прямой (возможно, расширенной) всегда можно указать непересекающиеся  - окрестности: - окрестности:  (это одно из свойств окрестностей). (это одно из свойств окрестностей).
По определению предела имеем:

Следовательно, при  , где , где  , все , все 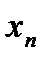 входят в обе окрестности входят в обе окрестности 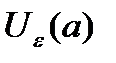 и и  , что невозможно, так как окрестности не пересекаются. Получившееся противоречие говорит о том, что предположение о двух различных пределах одной и той же последовательности является неверным. Следовательно, верно противоположное утверждение: последовательность может иметь только один предел. v , что невозможно, так как окрестности не пересекаются. Получившееся противоречие говорит о том, что предположение о двух различных пределах одной и той же последовательности является неверным. Следовательно, верно противоположное утверждение: последовательность может иметь только один предел. v
Предел стационарной последовательности
| Теорема о пределе стационарной последовательности
| Если все члены стационарной последовательности равны числу a, то существует предел этой последовательности, равный числу a:  . .
|
w Пусть  , тогда , тогда  будет будет  при при  ; ;
по определению конечного предела заключаем, что  , т.е. предел постоянной последовательности существует и равен этой постоянной. v , т.е. предел постоянной последовательности существует и равен этой постоянной. v
Переход к пределу в равенстве
| Теорема о переходе к пределу в равенстве
| Если члены двух последовательностей 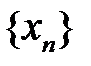 и и  совпадают (начиная хотя бы с некоторого номера совпадают (начиная хотя бы с некоторого номера  ) и обе эти последовательности имеют пределы, то их пределы равны:
если ) и обе эти последовательности имеют пределы, то их пределы равны:
если  . .
|
w  . Так как при всех . Так как при всех  верно равенство верно равенство 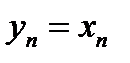 , то при , то при 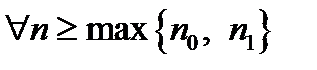 будет верно, что будет верно, что  , где , где  – это произвольное малое число. Отсюда на основании определения предела заключаем, что – это произвольное малое число. Отсюда на основании определения предела заключаем, что  . Так как последовательность может иметь только один предел, то . Так как последовательность может иметь только один предел, то  .v .v
Иллюстрация к свойству приведена на рис. 14:

Рис. 14
Другими словами это свойство можно сформулировать так:
в равенстве 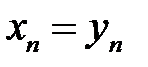 можно переходить к пределу: можно переходить к пределу: 
(при условии, что предел правой и левой частей существуют).
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 имеет конечный предел:
имеет конечный предел:  , то
, то 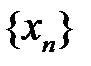 называется сходящейся последовательностью; в противном случае
называется сходящейся последовательностью; в противном случае  или
или 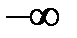 или
или  или не существует.
или не существует.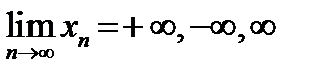 , то
, то  называется бесконечно большой последовательностью.
называется бесконечно большой последовательностью. , то
, то  ,
,  а также последовательность
а также последовательность  ; все эти последовательности являются также бесконечно малыми, потому что все они имеют пределом число 0.
; все эти последовательности являются также бесконечно малыми, потому что все они имеют пределом число 0. ,
,  , а также последовательность
, а также последовательность  являются расходящимися; из них бесконечно большой является только последовательность с общим членом
являются расходящимися; из них бесконечно большой является только последовательность с общим членом  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ;
;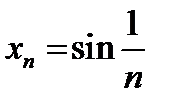 ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9) 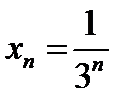 ; 10)
; 10)  .
. на координатной оси сделайте вывод о пределе
на координатной оси сделайте вывод о пределе  .
. предыдущего задания укажите номера сходящихся, расходящихся, бесконечно больших и бесконечно малых последовательностей.
предыдущего задания укажите номера сходящихся, расходящихся, бесконечно больших и бесконечно малых последовательностей. ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;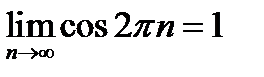 ; 6)
; 6)  ; 7)
; 7) 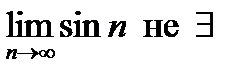 ; 8)
; 8) 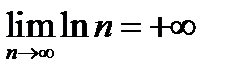 ;
; ; 10)
; 10)  .
. , то этот предел является единственным
, то этот предел является единственным
 имеет два различных предела:
имеет два различных предела: 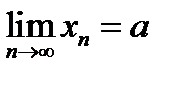 и
и  .
. - окрестности:
- окрестности:  (это одно из свойств окрестностей).
(это одно из свойств окрестностей).
 , где
, где  , все
, все 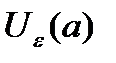 и
и  , что невозможно, так как окрестности не пересекаются. Получившееся противоречие говорит о том, что предположение о двух различных пределах одной и той же последовательности является неверным. Следовательно, верно противоположное утверждение: последовательность может иметь только один предел. v
, что невозможно, так как окрестности не пересекаются. Получившееся противоречие говорит о том, что предположение о двух различных пределах одной и той же последовательности является неверным. Следовательно, верно противоположное утверждение: последовательность может иметь только один предел. v .
.
 , тогда
, тогда  будет
будет  при
при  ;
; , т.е. предел постоянной последовательности существует и равен этой постоянной. v
, т.е. предел постоянной последовательности существует и равен этой постоянной. v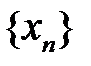 и
и  совпадают (начиная хотя бы с некоторого номера
совпадают (начиная хотя бы с некоторого номера  ) и обе эти последовательности имеют пределы, то их пределы равны:
если
) и обе эти последовательности имеют пределы, то их пределы равны:
если  .
.
 . Так как при всех
. Так как при всех  верно равенство
верно равенство 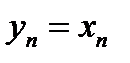 , то при
, то при 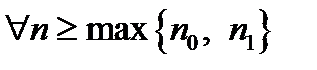 будет верно, что
будет верно, что  , где
, где  – это произвольное малое число. Отсюда на основании определения предела заключаем, что
– это произвольное малое число. Отсюда на основании определения предела заключаем, что  . Так как последовательность может иметь только один предел, то
. Так как последовательность может иметь только один предел, то  .v
.v
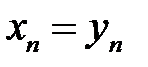 можно переходить к пределу:
можно переходить к пределу: 