Основные теоремы о бесконечно больших последовательностях
| Теорема о сумме двух бесконечно больших последовательностей
| Если две последовательности  и и  являются бесконечно большими при являются бесконечно большими при  и все их члены и все их члены  и и  при этом имеют одинаковый знак, то их сумма при этом имеют одинаковый знак, то их сумма  также является бесконечно большой последовательностью при также является бесконечно большой последовательностью при  . .
| w По определению бесконечно большой последовательности имеем:

Тогда при номерах  , где , где  верно неравенство верно неравенство
 . .
Теперь используем известное свойство модуля:  , причем , причем  только тогда, когда только тогда, когда  и и  имеют одинаковые знаки. По условию теоремы числа имеют одинаковые знаки. По условию теоремы числа 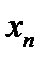 и и  имеют одинаковые знаки, поэтому имеют одинаковые знаки, поэтому  . .
Следовательно, при  верно неравенство верно неравенство  , где , где 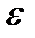 - это произвольное малое число. Это означает, что - это произвольное малое число. Это означает, что  , то есть последовательность , то есть последовательность  является бесконечно большой при является бесконечно большой при  . v . v
| Теорема о сумме бесконечно большой и ограниченной последовательностей
| Если последовательность  является бесконечно большой при является бесконечно большой при  и последовательность и последовательность  является ограниченной, то их сумма является ограниченной, то их сумма  является бесконечно большой последовательностью при является бесконечно большой последовательностью при  . .
|
w Запишем определения ограниченной последовательности и бесконечно большой последовательности:
1)  – ограниченная – ограниченная  число число  при при  ; ;
очевидно, что из неравенства  следует неравенство следует неравенство  ; ;
2)  – б. б. – б. б.  , ,
где  – сколь угодно малое число; если обозначить – сколь угодно малое число; если обозначить  , то определение , то определение
бесконечно большой последовательности можно записать несколько иначе:
 , ,
где M – сколь угодно большое число.
Теперь рассмотрим 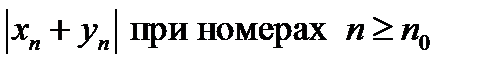 , используя при этом известное свойство модуля , используя при этом известное свойство модуля  : :
 . .
Таким образом, показано, что для любого числа  , сколь большим бы его ни брать, существует номер , сколь большим бы его ни брать, существует номер  такой, что при такой, что при  выполняется неравенство выполняется неравенство  . По определению бесконечного предела это означает, что . По определению бесконечного предела это означает, что  , то есть последовательность , то есть последовательность  является бесконечно большой при является бесконечно большой при  .v .v
| Теорема о произведении бесконечно больших последовательностей
| Если две последовательности  и и 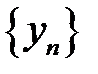 являются бесконечно большими при являются бесконечно большими при  , то их произведение , то их произведение  также есть бесконечно большая последовательность при также есть бесконечно большая последовательность при  . .
|
w Для доказательства запишем определения пределов обеих бесконечно больших последовательностей:

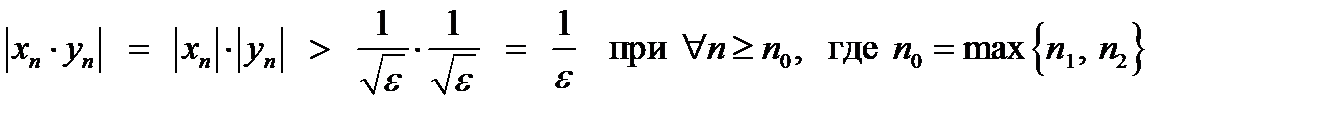 ; ;
таким образом, показано, что 
 – бесконечно большая последовательность при – бесконечно большая последовательность при  . v . v
| Теорема о связи бесконечно большой последовательности с бесконечно малой последовательностью
| Если  бесконечно большая последовательность при бесконечно большая последовательность при  и и  , то последовательность , то последовательность  является бесконечно малой при является бесконечно малой при  . .
|
w Записываем определение предела бесконечно большой последовательности:
 – б.б. – б.б.  при при  . .
Переходим к неравенству обратных величин:  при при  , учитывая, что , учитывая, что
 . Используя свойство модуля, получаем, что верно неравенство . Используя свойство модуля, получаем, что верно неравенство  при при
 для любого числа для любого числа  , сколь малым бы оно ни было; это означает по , сколь малым бы оно ни было; это означает по
определению предела, что 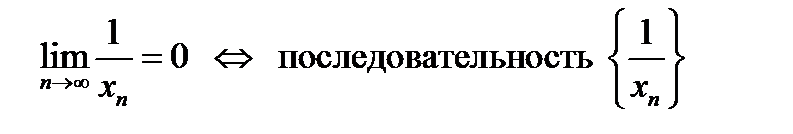 является является
бесконечно малой при  .v .v
| Теорема о произведении бесконечно большой последовательности на ограниченную последовательность
| Если последовательность 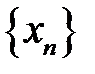 бесконечно большая при бесконечно большая при  , последовательность , последовательность  ограниченная, но не является бесконечно малой, и все её члены отличны от нуля (хотя бы начиная с некоторого номера ограниченная, но не является бесконечно малой, и все её члены отличны от нуля (хотя бы начиная с некоторого номера  ),
то произведение этих последовательностей ),
то произведение этих последовательностей  есть бесконечно большая последовательность при есть бесконечно большая последовательность при  . .
|
w Поработаем с ограниченной последовательностью  : учитывая, что она не является бесконечно малой и что все её члены отличны от нуля (хотя бы начиная с некоторого номера : учитывая, что она не является бесконечно малой и что все её члены отличны от нуля (хотя бы начиная с некоторого номера  ), при ), при  можно зафиксировать ограниченность членов этой последовательности по модулю: можно зафиксировать ограниченность членов этой последовательности по модулю:  , где a и b – положительные числа; , где a и b – положительные числа;
перейдем к неравенству обратных величин и получим, что  , ,
то есть последовательность  также является ограниченной. также является ограниченной.
Теперь поработаем с бесконечно большой последовательностью  . Так как числа . Так как числа  становятся сколь угодно большими (по модулю) при достаточно больших номерах становятся сколь угодно большими (по модулю) при достаточно больших номерах  , то можно предположить, что среди чисел , то можно предположить, что среди чисел  нет равных нулю, поэтому последовательность из их обратных величин нет равных нулю, поэтому последовательность из их обратных величин  может быть образована и является бесконечно малой (по теореме о связи бесконечно большой последовательности с бесконечно малой последовательностью). Очевидно, что также является бесконечно малой и следующая последовательность из модулей может быть образована и является бесконечно малой (по теореме о связи бесконечно большой последовательности с бесконечно малой последовательностью). Очевидно, что также является бесконечно малой и следующая последовательность из модулей  . .
Рассмотрим модуль произведения величин  и и  : : 
в знаменателе имеем произведение бесконечно малой последовательности  на ограниченную последовательность на ограниченную последовательность  ; по теоремам о бесконечно малых величины ; по теоремам о бесконечно малых величины  образуют бесконечно малую последовательность, тогда обратные им величины образуют бесконечно малую последовательность, тогда обратные им величины  образуют бесконечно большую последовательность; следовательно, последовательность образуют бесконечно большую последовательность; следовательно, последовательность  является бесконечно большой при является бесконечно большой при 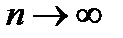 . v . v
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 и
и  являются бесконечно большими при
являются бесконечно большими при  и все их члены
и все их члены  и
и  при этом имеют одинаковый знак, то их сумма
при этом имеют одинаковый знак, то их сумма  также является бесконечно большой последовательностью при
также является бесконечно большой последовательностью при 
 , где
, где  верно неравенство
верно неравенство .
. , причем
, причем  только тогда, когда
только тогда, когда  и
и  имеют одинаковые знаки. По условию теоремы числа
имеют одинаковые знаки. По условию теоремы числа 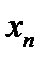 и
и  имеют одинаковые знаки, поэтому
имеют одинаковые знаки, поэтому  .
. верно неравенство
верно неравенство  , где
, где 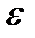 - это произвольное малое число. Это означает, что
- это произвольное малое число. Это означает, что  , то есть последовательность
, то есть последовательность  является бесконечно большой при
является бесконечно большой при  . v
. v является бесконечно большой при
является бесконечно большой при  является ограниченной, то их сумма
является ограниченной, то их сумма  – ограниченная
– ограниченная  число
число  при
при  ;
; следует неравенство
следует неравенство  ;
; – б. б.
– б. б.  ,
, – сколь угодно малое число; если обозначить
– сколь угодно малое число; если обозначить  , то определение
, то определение ,
,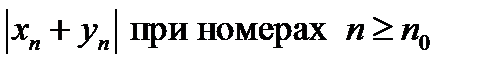 , используя при этом известное свойство модуля
, используя при этом известное свойство модуля  :
: .
. , сколь большим бы его ни брать, существует номер
, сколь большим бы его ни брать, существует номер  такой, что при
такой, что при  выполняется неравенство
выполняется неравенство  . По определению бесконечного предела это означает, что
. По определению бесконечного предела это означает, что  , то есть последовательность
, то есть последовательность  является бесконечно большой при
является бесконечно большой при  .v
.v и
и 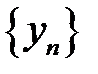 являются бесконечно большими при
являются бесконечно большими при  , то их произведение
, то их произведение  также есть бесконечно большая последовательность при
также есть бесконечно большая последовательность при 
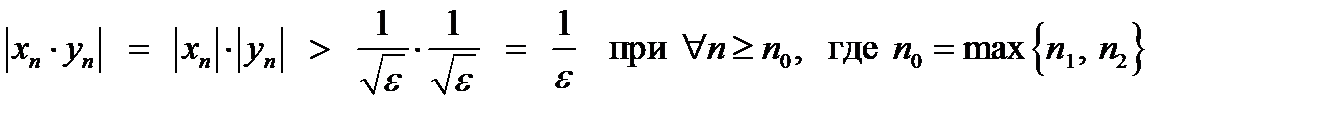 ;
;
 – бесконечно большая последовательность при
– бесконечно большая последовательность при  . v
. v бесконечно большая последовательность при
бесконечно большая последовательность при  и
и  , то последовательность
, то последовательность  является бесконечно малой при
является бесконечно малой при  – б.б.
– б.б.  при
при  .
. при
при  . Используя свойство модуля, получаем, что верно неравенство
. Используя свойство модуля, получаем, что верно неравенство  при
при , сколь малым бы оно ни было; это означает по
, сколь малым бы оно ни было; это означает по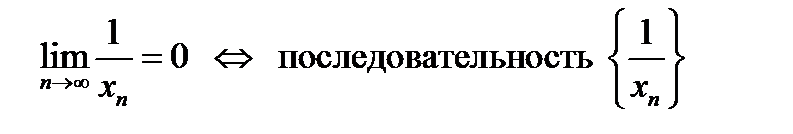 является
является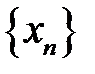 бесконечно большая при
бесконечно большая при  , последовательность
, последовательность  ограниченная, но не является бесконечно малой, и все её члены отличны от нуля (хотя бы начиная с некоторого номера
ограниченная, но не является бесконечно малой, и все её члены отличны от нуля (хотя бы начиная с некоторого номера  ),
то произведение этих последовательностей
),
то произведение этих последовательностей  есть бесконечно большая последовательность при
есть бесконечно большая последовательность при  .
.
 : учитывая, что она не является бесконечно малой и что все её члены отличны от нуля (хотя бы начиная с некоторого номера
: учитывая, что она не является бесконечно малой и что все её члены отличны от нуля (хотя бы начиная с некоторого номера  ), при
), при  можно зафиксировать ограниченность членов этой последовательности по модулю:
можно зафиксировать ограниченность членов этой последовательности по модулю:  , где a и b – положительные числа;
, где a и b – положительные числа; ,
,  также является ограниченной.
также является ограниченной. . Так как числа
. Так как числа  становятся сколь угодно большими (по модулю) при достаточно больших номерах
становятся сколь угодно большими (по модулю) при достаточно больших номерах  , то можно предположить, что среди чисел
, то можно предположить, что среди чисел  может быть образована и является бесконечно малой (по теореме о связи бесконечно большой последовательности с бесконечно малой последовательностью). Очевидно, что также является бесконечно малой и следующая последовательность из модулей
может быть образована и является бесконечно малой (по теореме о связи бесконечно большой последовательности с бесконечно малой последовательностью). Очевидно, что также является бесконечно малой и следующая последовательность из модулей  .
. :
: 
 на ограниченную последовательность
на ограниченную последовательность  ; по теоремам о бесконечно малых величины
; по теоремам о бесконечно малых величины  образуют бесконечно малую последовательность, тогда обратные им величины
образуют бесконечно малую последовательность, тогда обратные им величины  образуют бесконечно большую последовательность; следовательно, последовательность
образуют бесконечно большую последовательность; следовательно, последовательность  является бесконечно большой при
является бесконечно большой при 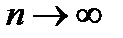 . v
. v