|
Концепция численного интегрирования
Пусть требуется найти определенный интеграл  от непрерывной функции от непрерывной функции  . Если можно найти первообразную . Если можно найти первообразную  функции функции  , то интеграл вычисляют по формуле Ньютона-Лейбница: , то интеграл вычисляют по формуле Ньютона-Лейбница:  . .
При этом могут возникнуть следующие трудности:
- отыскание первообразной весьма сложно;
- не любая непрерывная функция и её первообразная выражаются элементарными функциями;
- функция  задана графически или таблично. задана графически или таблично.
В таких случаях для вычисления определенного интеграла прибегают к приближенным формулам, с помощью которых определенный интеграл можно найти с любой степенью точности.
Наиболее используемыми являются следующие формулы приближенного вычисления определённого интеграла:
- формула прямоугольников;
- формула трапеций;
- формула парабол (формула Симпсона).
Формула прямоугольников
Пусть на отрезке  задана непрерывная функция задана непрерывная функция  . Требуется вычислить определенный интеграл . Требуется вычислить определенный интеграл  , численно равный площади соответствующей криволинейной трапеции. , численно равный площади соответствующей криволинейной трапеции.
Разобьем основание этой трапеции, т.е. отрезок  , на , на  равных частей (частичных отрезков) точками равных частей (частичных отрезков) точками  . Длина каждого отрезка равна . Длина каждого отрезка равна  , где , где  (рис. 6). (рис. 6).
В середине  каждого отрезка построим ординату каждого отрезка построим ординату  графика функции графика функции  . Приняв эту ординату за высоту, построим прямоугольник с площадью . Приняв эту ординату за высоту, построим прямоугольник с площадью  . .
Сумма площадей всех  прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла: прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла:
 . (5.1) . (5.1)

Рис. 6.
Погрешность формулы (5.1) оценивается с помощью формулы:
 (5.2) (5.2)
где  – наибольшее значение второй производной на отрезке – наибольшее значение второй производной на отрезке  . .
Пример 9.
Вычислить интеграл  с помощью формулы прямоугольников, разбив отрезок интегрирования на 8 частей. с помощью формулы прямоугольников, разбив отрезок интегрирования на 8 частей.
Решение.
По условию a = 1, b = 2, n = 8,  . .
Таблица 5.1
| i
| 
| 
| 
| |
| 1,000
|
|
| |
| 1,125
| 1,0625
| 0,780377
| |
| 1,250
| 1,1875
| 0,408854
| |
| 1,375
| 1,3125
| -0,033996
| |
| 1,500
| 1,4375
| -0,457565
| |
| 1,625
| 1,5625
| -0,786985
| |
| 1,750
| 1,6875
| -0,970745
| |
| 1,875
| 1,8125
| -0,985006
| |
| 2,000
| 1,9375
| -0,834274
| |
|
| 
| -2,879340
|  . .
Оценим погрешность найденного значения. Найдем вторую производную функции 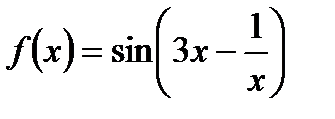 , ,
 , ,
 , ,
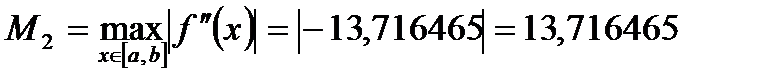 . .
Следовательно, 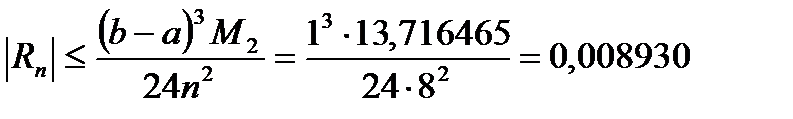 . .
Ответ:  . .
Формула трапеций
Формулу трапеций получают аналогично формуле прямоугольников, заменяя на каждом частичном отрезке криволинейную трапецию обычной.
Разобьем основание криволинейной трапеции, т.е. отрезок  , на , на  равных частичных отрезков длины равных частичных отрезков длины  . Абсциссы точек деление . Абсциссы точек деление  (рис. 7). Пусть (рис. 7). Пусть  – соответствующие им ординаты графика функций. В этом случае будут иметь место формулы: – соответствующие им ординаты графика функций. В этом случае будут иметь место формулы:  , ,  , где , где  . .
Заменим кривую  ломаной линией, звенья которой соединяют концы ординат ломаной линией, звенья которой соединяют концы ординат  и и  где где  . Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями . Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями 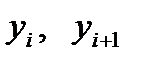 , где , где  , и высотой , и высотой  : :
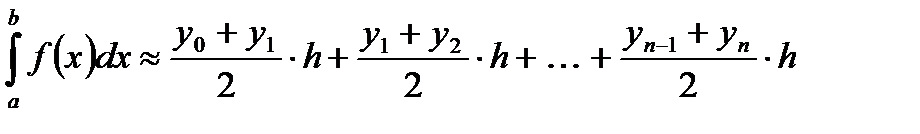
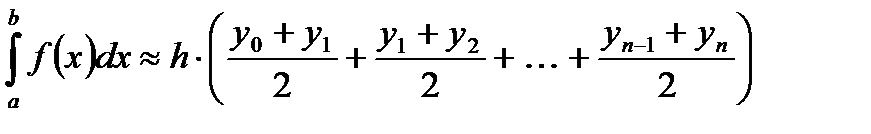
или
 . (5.3) . (5.3)
Погрешность формулы (5.3) оценивается с помощью формулы:
 (5.4) (5.4)
где  – наибольшее значение второй производной на отрезке – наибольшее значение второй производной на отрезке  . .

Рис. 7.
Пример 10.
Условие задачи сформулировано в примере 9.
Решение.
По условию a = 1, b = 2, n = 8.
Таблица 5.2
| i
| 
| 
| |
| 1,000
| 0,909297
| |
| 1,125
| 0,609541
| |
| 1,250
| 0,190423
| |
| 1,375
| -0,253343
| |
| 1,500
| -0,637879
| |
| 1,625
| -0,899237
| |
| 1,750
| -0,999428
| |
| 1,875
| -0,928932
| |
| 2,000
| -0,705540
| 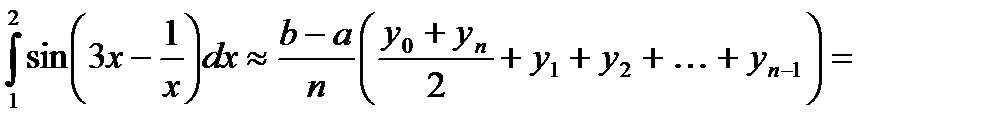
 . .
Оценим погрешность найденного значения.
Из примера 9:
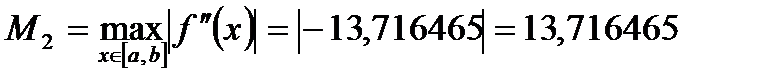 . .
Следовательно,  . .
Ответ:  . .
Формула парабол (Симпсона)
Если заменить график функции 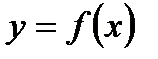 на каждом отрезке на каждом отрезке  разбиения не отрезками прямых, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла разбиения не отрезками прямых, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла  . .
Предварительно найдем площадь  криволинейной трапеции, ограниченной сверху графиком параболы криволинейной трапеции, ограниченной сверху графиком параболы  , сбоку – прямыми , сбоку – прямыми  , ,  и снизу – отрезком и снизу – отрезком  . Пусть парабола проходит через три точки . Пусть парабола проходит через три точки  , ,  , ,  (рис. 8), где (рис. 8), где
 – ордината параболы в точке – ордината параболы в точке  ; (5.5) ; (5.5)
 – ордината параболы в точке – ордината параболы в точке  ; (5.6) ; (5.6)
 – ордината параболы в точке – ордината параболы в точке  . (5.7) . (5.7)
Площадь  равна равна
 . (5.8) . (5.8)

Рис. 8.
Из формул (5.5), (5.6) и (5.7) выразим коэффициенты  и подставим их в формулу (5.8). В результате получим: и подставим их в формулу (5.8). В результате получим:
 (5.9) (5.9)
Теперь получим формулу парабол для вычисления интеграла  . .
Для этого отрезок  разобьём на разобьём на  равных частей (отрезков) длиной равных частей (отрезков) длиной  точками точками  . В точках деления . В точках деления  вычисляем значение подынтегральной функции вычисляем значение подынтегральной функции 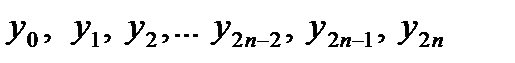 , где , где  (рис. 9). (рис. 9).

Рис. 9.
Заменяем каждую пару соседних элементарных трапеций с основаниями, равными  , одной элементарной параболической трапецией с основанием, равным , одной элементарной параболической трапецией с основанием, равным  . На отрезке . На отрезке 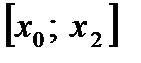 парабола проходит через три точки парабола проходит через три точки  , ,  , ,  . Используя формулу (5.9) находим площадь параболической трапеции . Используя формулу (5.9) находим площадь параболической трапеции
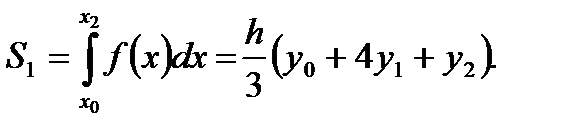
Аналогично находим
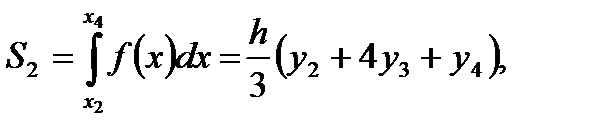

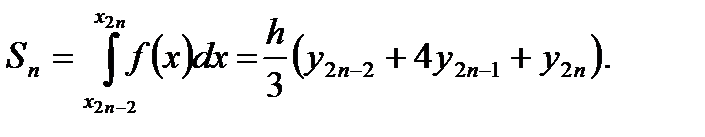
Сложив полученные равенства, получим:
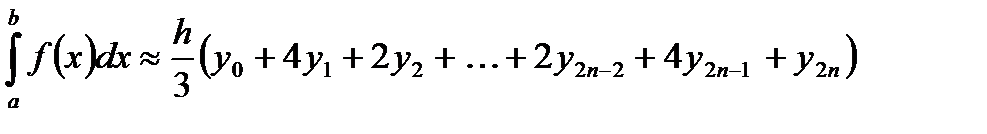
или
 . (5.10) . (5.10)
Погрешность формулы (5.10) оценивается с помощью формулы:
 (5.11) (5.11)
где  – наибольшее значение четвертой производной на отрезке – наибольшее значение четвертой производной на отрезке  . .
Пример 11.
Условие задачи сформулировано в примере 9.
Решение.
По условию a = 1, b = 2, n = 8,  . .
Таблица 5.3
| i
| 
| 
| 
| 
| 
| |
| 1,000
| 0,909297
| 0,909297
|
|
| |
| 1,0625
| 0,780377
|
| 0,780377
|
| |
| 1,1250
| 0,609541
|
|
| 0,609541
| |
| 1,1875
| 0,408854
|
| 0,408854
|
| |
| 1,250
| 0,190423
|
|
| 0,190423
| |
| 1,3125
| -0,033996
|
| -0,033996
|
| |
| 1,3750
| -0,253343
|
|
| -0,253343
| |
| 1,4375
| -0,457565
|
| -0,457565
|
| |
| 1,500
| -0,637879
|
|
| -0,637879
| |
| 1,5625
| -0,786985
|
| -0,786985
|
| |
| 1,6250
| -0,899237
|
|
| -0,899237
| |
| 1,6875
| -0,970745
|
| -0,970745
|
| |
| 1,750
| -0,999428
|
|
| -0,999428
| |
| 1,8125
| -0,985006
|
| -0,985006
|
| |
| 1,8750
| -0,928932
|
|
| -0,928932
| |
| 1,9375
| -0,834274
|
| -0,834274
|
| |
| 2,000
| -0,705540
| -0,705540
|
|
| |
|
| ∑
| 0,203757
| -2,879340
| -2,918856
|  . .
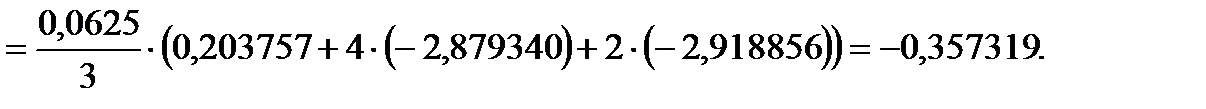
Оценим погрешность найденного значения. Найдем четвертую производную функции:
 , ,
 , ,
 , ,
 . .
 . .
Следовательно,  . .
Ответ:  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 от непрерывной функции
от непрерывной функции  . Если можно найти первообразную
. Если можно найти первообразную  функции
функции  .
. задана непрерывная функция
задана непрерывная функция  . Требуется вычислить определенный интеграл
. Требуется вычислить определенный интеграл  равных частей (частичных отрезков) точками
равных частей (частичных отрезков) точками  . Длина каждого отрезка равна
. Длина каждого отрезка равна  , где
, где  (рис. 6).
(рис. 6). каждого отрезка построим ординату
каждого отрезка построим ординату  графика функции
графика функции  .
. . (5.1)
. (5.1) (5.2)
(5.2) – наибольшее значение второй производной на отрезке
– наибольшее значение второй производной на отрезке  с помощью формулы прямоугольников, разбив отрезок интегрирования на 8 частей.
с помощью формулы прямоугольников, разбив отрезок интегрирования на 8 частей. .
.



 .
.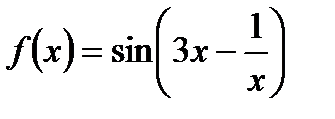 ,
, ,
, ,
,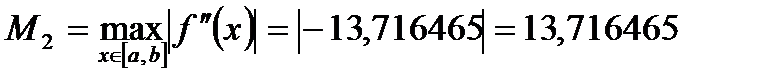 .
.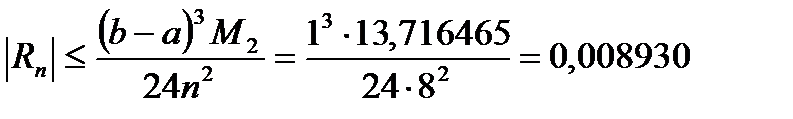 .
. .
. . Абсциссы точек деление
. Абсциссы точек деление  (рис. 7). Пусть
(рис. 7). Пусть  – соответствующие им ординаты графика функций. В этом случае будут иметь место формулы:
– соответствующие им ординаты графика функций. В этом случае будут иметь место формулы:  ,
,  , где
, где  .
. ломаной линией, звенья которой соединяют концы ординат
ломаной линией, звенья которой соединяют концы ординат  и
и  где
где 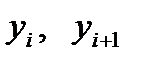 , где
, где  , и высотой
, и высотой 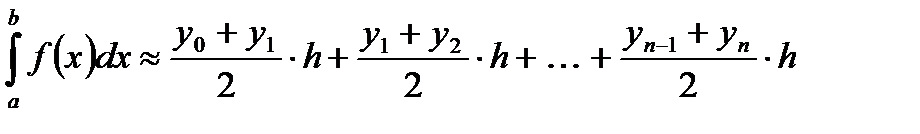
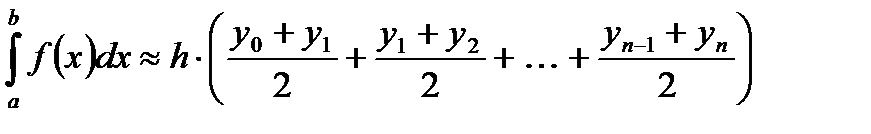
 . (5.3)
. (5.3) (5.4)
(5.4)
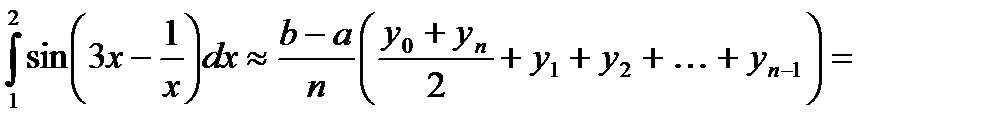
 .
. .
. .
.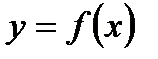 на каждом отрезке
на каждом отрезке  разбиения не отрезками прямых, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла
разбиения не отрезками прямых, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла  криволинейной трапеции, ограниченной сверху графиком параболы
криволинейной трапеции, ограниченной сверху графиком параболы  , сбоку – прямыми
, сбоку – прямыми  ,
,  и снизу – отрезком
и снизу – отрезком  . Пусть парабола проходит через три точки
. Пусть парабола проходит через три точки  ,
,  ,
,  (рис. 8), где
(рис. 8), где – ордината параболы в точке
– ордината параболы в точке  – ордината параболы в точке
– ордината параболы в точке  ; (5.6)
; (5.6) – ордината параболы в точке
– ордината параболы в точке  . (5.7)
. (5.7) равна
равна . (5.8)
. (5.8) и подставим их в формулу (5.8). В результате получим:
и подставим их в формулу (5.8). В результате получим: (5.9)
(5.9) равных частей (отрезков) длиной
равных частей (отрезков) длиной  точками
точками  . В точках деления
. В точках деления  вычисляем значение подынтегральной функции
вычисляем значение подынтегральной функции 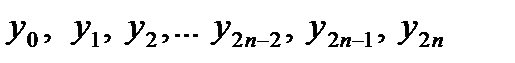 , где
, где  (рис. 9).
(рис. 9). , одной элементарной параболической трапецией с основанием, равным
, одной элементарной параболической трапецией с основанием, равным  . На отрезке
. На отрезке 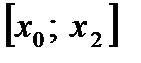 парабола проходит через три точки
парабола проходит через три точки  ,
,  ,
,  . Используя формулу (5.9) находим площадь параболической трапеции
. Используя формулу (5.9) находим площадь параболической трапеции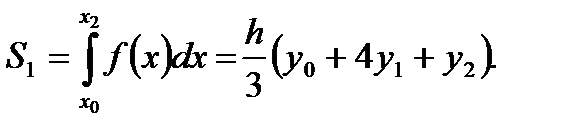
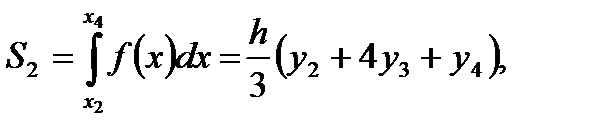

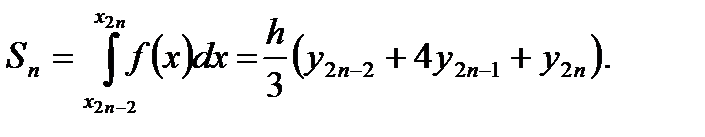
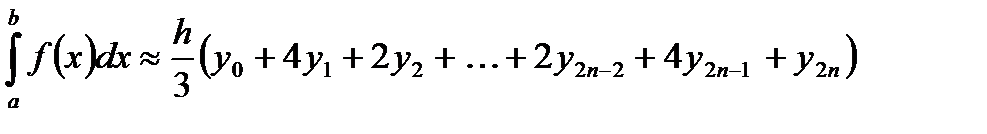
 . (5.10)
. (5.10) (5.11)
(5.11) – наибольшее значение четвертой производной на отрезке
– наибольшее значение четвертой производной на отрезке  .
.


 .
.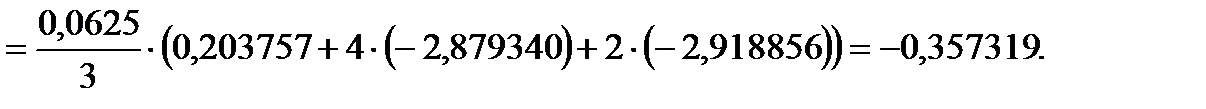
 ,
, ,
, .
. .
. .
. .
.